Python算法例20 最接近的k个数

1. 问题描述

给定一个目标数target，一个非负整数k，一个按照升序排列的数组A。在A中找出与target最接近的k个整数，返回这k个数并按照与target的接近程度从小到大排序，如果接近程度相当，那么值小的排在前面。

2. 问题示例

如果A=[1，2，3]，target=2，k=3，那么返回[2，1，3]；如果A=[1，4，6，8]，target=3，k=3，那么返回[4，1，6]。

3. 代码实现

使用二分查找和双指针的算法。

具体步骤如下：

1. 首先，使用二分查找在数组A中找到最接近target的数，记为closest。
2. 初始化两个指针：left指向closest的左边一个位置，right指向closest的右边一个位置。
3. 使用双指针向左右两边扩展，每次选择与target更接近的数，并将该数加入结果数组中。直到结果数组的长度达到k或者指针已经越界为止。
4. 如果结果数组的长度小于k，则根据与target的接近程度进行排序，返回前k个数，否则直接返回结果数组。

def findClosestElements(A, target, k):
    left = 0
    right = len(A) - 1

    # 二分查找最接近target的数
    while left < right:
        mid = (left + right) // 2
        if A[mid] == target:
            right = mid
            break
        elif A[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    # 左右指针向两边扩展，选择与target更接近的数
    while right - left + 1 < k:
        if left == 0:
            right += 1
        elif right == len(A) - 1:
            left -= 1
        else:
            if target - A[left - 1] <= A[right + 1] - target:
                left -= 1
            else:
                right += 1

    # 根据与target的接近程度进行排序
    result = sorted(A[left:right + 1], key=lambda x: (abs(x - target), x))
    return result[:k]
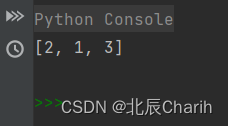
A=[1,2,3]
target=2
k=3
result = findClosestElements(A, target, k)
print(result)

?在这个实现中，首先使用二分查找找到最接近target的数closest。然后，初始化left和right指针，通过双指针向两边扩展，选择与target更接近的数并将其加入结果数组中。最后，如果结果数组的长度小于k，则根据与target的接近程度进行排序，返回前k个数，否则直接返回结果数组。

这个算法的时间复杂度为O(log(n)+k)，其中n为数组A的长度。首先，二分查找需要O(log(n))的时间复杂度，然后双指针的扩展需要O(k)的时间复杂度。