在排序数组中查找元素的第一个和最后一个位置

前言：

这是一道给很经典的二分查找题目，并且该二分查找的算法不同于简单二分，是二分查找的进阶版本。

一、题目描述

34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组?nums，和一个目标值?target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值?target，返回?[-1, -1]。

你必须设计并实现时间复杂度为?O(log n)?的算法解决此问题。

二、题目解析

注意只要数据中国可以找到具有二段性，即可适用二分查找算法！！！

我们将这道题拆解成两个部分，第一部分就是求该元素的左端点，另一部分就是求该元素的右端点。其实这两部分是大同小异，只要弄懂其中一个，另一个就迎刃而解！

我们首先来讲第一部分——求该元素的左端点。

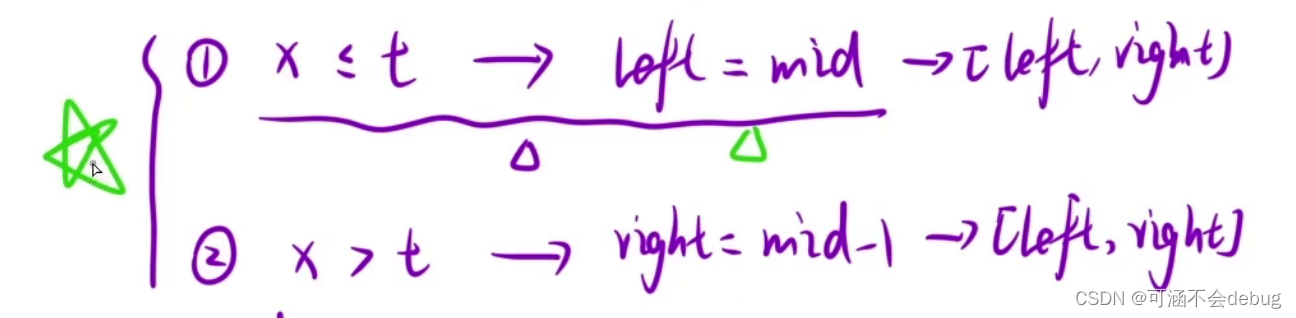
第一步将这些数据分为两个部分：小于元素和大于等于该元素这两个部分。

第二步就是普通二分算法的代码

注意这里有一个细节，跟普通二分查找算法不同，也是后面细节的“万恶之源”。就是当 x >= t 时，right = mid，而不是mid - 1，这是因为我们最开始是将数组分为两个部分，一部分就是大于等于该元素，如果right = mid - 1，又可能会将我们要求的数据筛掉，所以这里必须要用right = mid，而不是-1.

其实上面大体结构上是跟普通二分区别不大的，但下面的细节处理是进阶二分的精髓。

1、处理循环条件

这里的循环条件跟处理右端点是一致的，不能写等号，当判断等号时就会死循环！

2、求中点操作

首先我们要知道为了避免数据的溢出我们采用上面的求中点操作，而不是直接加，可能会数据的溢出。

然后上面的两种算法分别是求左边和右边。

求左端点为何采用第一种方法，求右端点为何采用第二种方法呢？
因为左端点是将数据分为小于和大于等于，所以right = mid，如果这里采用第二种求中点方法，就会造成死循环，right的值一直都没有变化！

上面就是讲解左端点的解法，右端点也是大同小异。

三、原码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size() == 0)
            return {-1,-1};
        //先找左端点，将数组分为小于和大于等于两部分
        int left = 0;
        int right = nums.size() - 1;
        int mid = 0;
        int begin = 0;
        while(left < right)//第一个小细节
        {
            mid = left + (right - left)/2;//第二个小细节
            if(nums[mid] < target)
                left = mid + 1;
            else
                right = mid;//万恶之源
        }
        if(nums[left] == target)
            begin = left;
        else
            return {-1,-1};
        left = 0;
        right = nums.size() - 1;
        //再找右端点，将数组分为小于等于和大于两个部分
        while(left < right)
        {
            mid = left + (right - left + 1)/2;
            if(nums[mid] <= target)
                left = mid;
            else
                right = mid - 1;
        }
        return {begin, right};
    }
};