Python和Java代码实现：切线法求解一维最优化问题

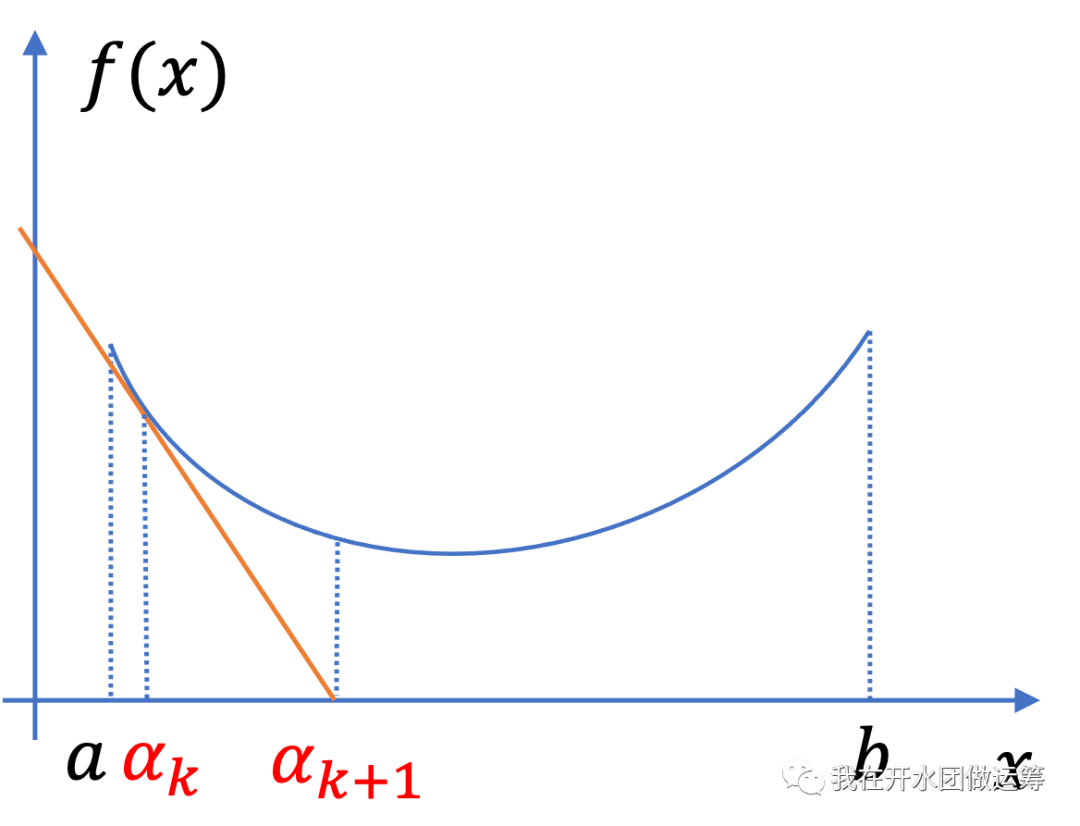
根据概念查询，切线法定义如下：
切线法（Tangent Method）是一种用于求解非线性方程的数值方法。它也被称为牛顿法（Newton’s Method），因为它是由艾萨克·牛顿发明的。

牛顿切线法是一种求解方程近似解的数值方法。它利用函数在某一点的切线来逼近函数的零点，从而得到方程的近似解。该方法的原理是：对于一个连续可导的函数，通过对函数图像上某一点处的切线进行截距求解，得到该点处的横坐标，然后将该横坐标代入函数中，得到新的函数值，重复以上步骤，直到函数值足够接近零点为止。

切线法的基本思想是通过在给定点的切线来逼近函数的根。具体来说，如果你有一个非线性方程 $f(x)=0$，并且你想找到该方程的根，你可以从一个初始猜测 $x_0$ 开始，然后通过以下步骤来迭代地逼近解：

1. 在点 $(x_0,f(x_0))$ 处画出函数的切线。

2. 找到这条切线与 $x$ 轴的交点，记作 $x_1$。

3. 将 $x_1$ 作为新的猜测，回到步骤1，重复这个过程。

这个过程的数学表达式是：

$$x_{n+1}=x_n?\frac{f(x_n)}{f^{\prime }(x_n)}$$

其中，$x_n$ 是第 $n$ 次迭代的解，$f^{\prime }(x_n)$ 是函数在 $x_n$ 处的导数。

需要注意的是，这个方法并不总是能够找到解，特别是当初始猜测离解很远，或者函数在解附近的性质使得迭代过程不收敛的时候。在实际应用中，通常会设置一个最大迭代次数和一个足够小的阈值，当连续两次迭代的解之间的差小于这个阈值时，就认为找到了足够精确的解。

我理解的，作者这里应该是首先将求最小值的问题转换成了求一阶导函数等于0的问题，因此是对一阶导函数应用切线法，因此才有一阶导和二阶导的计算

代码实现

Python代码

# 待优化函数  
def f(t):  
    return t ** 2 - t * 5 + 8  
  
  
# 待优化函数一阶导数  
def d_f(t):  
    return 2 * t - 5  
  
  
# 待优化函数二阶导数  
def d_2_f(t):  
    return 2  
  
  
# 切线法  
def tangent_method(x, eps):  
  
    cnt = 0  
    while abs(-d_f(x) / d_2_f(x)) > eps:  
        # 更新x，并增加迭代次数  
        x += -d_f(x) / d_2_f(x)  
        cnt += 1  
  
    return x, f(x), cnt  
  
  
if __name__ == '__main__':  
    # 参数设置  
    left_point = 1  
    right_point = 7  
    min_interval_value = 0.1  
  
    # 选取初始点  
    x0 = 6  
    # 调用切线法求解最小值  
    best_x, best_y, iter_cnt = tangent_method(x0, min_interval_value)  
    # 输出最优解  
    print('best_x: {}, best_y: {}, iter_cnt: {}.'.format(best_x, best_y, iter_cnt))  
  

Java代码

以下的tangentMethod函数为切线法的Java代码。

public class TangentMethod {  
  
    public static void main(String[] args) {  
        // 参数设置  
        int leftPoint = 1;  
        int rightPoint = 7;  
        double minIntervalValue = 0.1;  
  
        double x0 = 6.0;  
        Solution best_solution = tangentMethod(x0, minIntervalValue);  
        System.out.println("best_x: " + best_solution.best_x);  
        System.out.println("best_y: " + best_solution.best_y);  
        System.out.println("cnt: " + best_solution.cnt);  
    }  
  
    // 切线法  
    private static Solution tangentMethod(double x, double eps) {  
        // 统计迭代次数  
        int cnt = 0;  
  
        while (Math.abs(df(x) / d2f(x)) > eps) {  
            // 更新x，并增加迭代次数  
            x -= df(x) / d2f(x);  
            cnt ++;  
        }  
  
        // 构造最优解对象  
        Solution best_solution = new Solution();  
        best_solution.best_x = x;  
        best_solution.best_y = f(x);  
        best_solution.cnt = cnt;  
  
        return best_solution;  
    }  
  
    // 待优化函数  
    private static double f(double t) {  
        return t * t - t * 5 + 8;  
    }  
  
    // 待优化函数一阶导数  
    private static double df(double t) {  
        return t * 2 - 5;  
    }  
  
    // 待优化函数二阶导数  
    private static double d2f(double t) {  
        return 2;  
    }  
  
    // 解对象  
    private static class Solution {  
        double best_x;  
        double best_y;  
        int cnt;  
    }  
}  
  

求解实例

无论运行Python程序还是Java程序，可以得到最优解如下：

best_x: 2.5, best_y: 1.75, iter_cnt: 1.  

从结果上可以看出，切线法只需要迭代一次即可得到最优解；而使用黄金分割法需要迭代的次数为9。这主要是因为切线法使用了待优化函数更多的信息，包括一阶和二阶导数，所以计算效率更高，这在文章中也有提到过该理论。

此外，相比黄金分割法，切线法并不依赖左右端点的值，但是会对初值更加敏感（虽然文中的实例对初值不敏感），这也是值得注意的。