模拟IC设计-学习笔记

写在前面：本文是我自己学习b站上up主(jrilee讲电路)的模集课程时记的笔记，原课程：模拟IC设计 第一讲 -- Device and modeling (I)_哔哩哔哩_bilibili

目录

器件基础

求输出电阻

MOS管的小信号模型，拉扎维书上常用的是π模型，计算的更精确，下面的T模型适用于更直观的分析，毕竟有的时候并不需要计算的那么精确。

MOS管饱和区和三极管区的电流公式。gm的三个公式。ro就是在饱和区曲线的斜率的倒数。λ和L成反比。

如果想要一个电流源，那么希望饱和区的曲线越平越好，即希望斜率越小越好，也就是希望ro越大越好，那么就希望λ越小越好，L越大越好。所以如果是差分对的话，那么差分对的L可能是最小L，因为需要高速的性能。但是差分对的尾电流源的L要是最小L的N倍，才能使电流源稳定。

S端和D端没有固定区分，电压低的一端自然是S端。要定位P+区body极的电压，将载流子都吸引过来，否则p_sub不同区域有较大的电压偏差，如果B和S不在同一个电位，那么G极就需要更高的电压把载流子拉过去。这就是体效应。所以差分对的输入对管存在体效应。

PMOS，B电极是独立定义的，每一个n-well是一个独立的cell，所以是可以将B和S接到一起的，不受体效应影响。

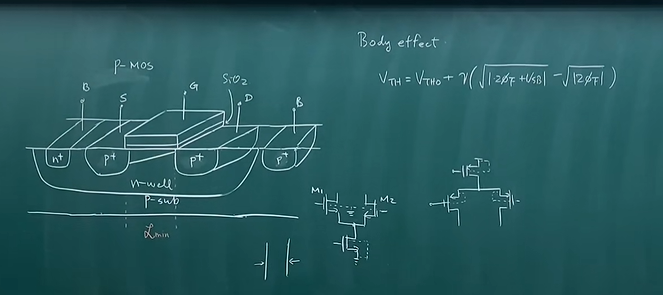
定义了最小沟道长度Lmin。W，与W和L的乘积，即栅极面积有关。

定义：对于一个MOS来说，为栅极寄生电容。在输入端施加一个电流源，那么经过放大，漏端的电流源是要比栅端的电流要大的，。但是随着频率的上升，变得越来越小，所以阻抗和电流源的乘积在变小，那么也在变小。当时，即为截止频率。在这个频率之后，MOS管不再有放大的效果。

当制程以0.7倍缩小时，其WL的面积是以0.5倍缩小。那么缩小，截止频率增加。

制程缩小的缺点：

不匹配性mismatch越来越大，会产生offset。随着制程的缩小，VDD也越来越小，会导致很多电路无法设计。

在28nm制程以下出现的是FinFET。

MOS导通电阻-作为开关

尺寸越大，导通电流越大，导通电阻越小。

MOS开关的好处：可以完全关掉，，漏端和源端可互换。

Bipolar

单级放大器的频率响应

在180nm以下，由于速度饱和，MOS电流电压不再是二次方的关系，而会提前达到饱和。

每个电容都会产生一个零点和一个极点。

有些零点会消失，跑到无限远的地方去。

分析其中的一个电容时，当做爱他电容不存在或短路。

零点：找到一个频率，在这个频率下无论输入是什么，输出都是0。

小信号模型

考虑Cc1存在的情况，Cc2和Cs短路，所以小信号变成下图。极点很容易得到，注意栅极电流为0。零点：要找到一个值使输入不管怎么边，输出都为0。输出为0V，所以要让输出电流为0，所以要求VP=0V。只有Cc1开路的时候，无论输入是多少，VP=0V，所以要使无穷大，那么零点就为0。

当时，零点。

考虑Cs存在的情况

考虑Cc2存在的情况

零点：要是Cc2无限大

第二零点比第二极点小，但是跟第一极点和第三极点的位置不确定，这里先假设第二级点比所有极点都小。

MOS寄生电容

带宽由电路内部寄生电容决定，在由前面的波特图保持平稳一段时间后，由于寄生电容的存在，增益开始往下掉。

共源极

通过密勒效应等效，找极点。

另一种计算方法，当考虑一个电容时，认为其他电容不存在，那么极点就有该电容和看出去的阻抗相乘的倒数，带宽就等于所有这样的电容跟阻抗相乘的和的倒数。

当只考虑Cgs时，电阻是Rsig。得到第一个极点

只考虑Cgd时，通过将Cgs看成一个电压源，求其往外看的等效电阻，那么等效电阻就是电压/电流=Vt/It，即可得到第二级点。

将两个极点对应的RC相加再求倒数就是带宽。

得到的带宽结果跟上面的方法得到的带宽有些许差距，但是影响不大。密勒效应得到的结果比较直观，便于分析，但是精确性不如下图的方法。

上面讲的是极点，现在求零点。求一个电容的零点时，忽略其他电容，找到无论输入是什么，输出都为0的频率，就是零点。

Vout=0V，那么电流为0，gmVgs=0，则Vgs=0，需要使Cgs阻抗无穷小，即Cgs无穷大。则可以得到Cgs带来的零点。

同样的方法可以求得Cgd的零点，对s取符号就是零点的位置，可以看到s是位于右半平面的。

左半平面的零点，也就是S为负值，为正值，是正常的零点，相位会在该零点向上抬高90°。电路由足够的相位裕度。

左半平面的零点，也就是S为正值，为负值，该零点会导致相位恶化90°，所以已经没有相位裕度了。

但是对于此共源极电路来说，相比于两个极点来说，零点在很远的位置。所以在增益会很快以-40dB/十倍频的速度往下掉，很快就掉到0dB，所以零点的位置是在0dB之外的，因此不会影响相位裕度。

共栅级

对于Cgs，电容乘电阻，电阻是Rsig和向右看的阻抗的并联，向右看的阻抗约等于1/gm。

考虑Cgd，那么阻抗就是Req和RD的并联，这个Req很好算，就相当于带源极内阻的共源极的输出阻抗，这个阻抗的值是大于RD的，所以并联之后最终的阻抗就是RD。

这Cgs和Cgd带来的两个极点都是工作在比较高的频率，所以共栅级是可以工作在比较高的频率的。

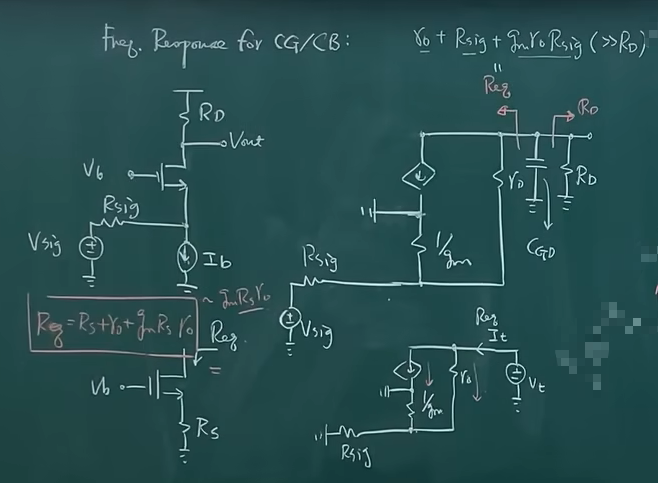
零点

求Cgs零点，要使Vout=0，则需要使其电流为0，栅极电流为0，那么需要流过1/gm的电流也为0，则需要Cgs的阻抗无穷小，那么零点无穷大。

求Cgd零点，要使Vout=0，那么Cgd两端都为0电位，则需要使Cgd的阻抗为0，则零点无穷大。

共栅级的两个零点都在无穷远处，所以传输函数的分子为1。

共源共栅

影响带宽的点主要就是M1的栅极这个点，所以需要将Cgd等效，共M1的增益为-1，因为其负载电阻为1/gm。所以可以得到等效电容为2Cgd。

共漏极

共漏极的增益接近于1，多以常常被当做buffer使用。

buffer缓冲级，一般前一级的增益要求非常大，因为前一级的输出阻抗非常大，如果前一级直接接负载电阻，那么其输出阻抗比负载电阻还要大，并联之后的值更倾向于负载电阻，那么整体增益就会受到负载电阻的影响而减小。

此时就需要个buffer，buffer的输入电阻无穷大，输出电阻为1/gm比较小。因此，输出阻抗与负载电阻并联之后的值不会受到负载电阻的影响，因此，增益不会受到负载电阻的影响。

求Cgs的极点，将Cgs看成测试信号，求其往外看的阻抗。

求Cgs零点，Vout=0V，那么Cgs两端的电压就是Vout-i*(1/gm)，即可求得零点。

求Cgd的极点，其等效输出阻抗就是Rsig。

求零点，Vout=0V，那么流过1/gm的电流也为0，所以要求所有电流都流过Cgd，那么要求Cgd的阻抗为0，即可求出零点。

两个极点的分母相加再求倒数就是带宽。

这个电路有可能会存在不稳定的情况，在频率比较高的时候要考虑寄生电容。由于Cgd比较小，所以这里只考虑Cgs存在的情况。

通过计算其输出阻抗可以看出，输出阻抗有一个零点和一个极点，那么输出阻抗就是一个随着频率变化的值。一开始我们希望的buffer是其输出阻抗为1/gm比较小。但是这个buffer的输出阻抗在低频的时候是1/gm，在高频的时候会遇到零点和极点，其输出阻抗会变化。所以其输出阻抗类似于一个电感。电感输入一个方波的时候，输出会有振铃。所以bipolar作为buffer，因为其VBE固定，那么栅极电容就是固定的。但是CMOS作为buffer，其Vgs不固定，那么Cgs也是不固定的。

源极负反馈

好处：自偏置，提高线性度，当做均衡器使用。

线性度，增加RE这个电阻，可以增加差分对线性工作的范围。

均衡器，当漏端有一个寄生电容存在的时候，增益经过这个极点就会往下掉。但是添加RE和CS之后，往外产生一个零点和一个极点，会先将增益拉高，最后遇到两个极点再往下掉。如果只关心特定频率以内的增益的话，这个电路可以使特定频率以内的增益保持均衡。

该电路还有反馈的作用，给一个输入电压，经过MOS转换成电流，电流在RS产生压降，反馈给输入，Vin-这个压降再输入给MOS。

右图也是反馈，只不是反馈回来是电流加减，左图反馈回来是电压加减。

练习：

输入经过运放之后再经过源极跟随器电压，再经过Q1/Q2是共射极放大电路。Q5/Q6也是共射极放大电路。Q3是保护作用，当Q5发射极电压太高的时候，Q3导通将Q5基极电流放掉，拉低电压，保护Q5，Q4作用同理。输入端的两个二极管是起保护作用。

上图中3.3k和100k的电阻构成反馈，所以所以第二级增益为31。

vout经过100k和5k的电阻反馈到输入，所以整体的全局增益是21。

差动对

差动对的线性范围比bipolar大。求线性区边界的时候，所有电流流过M1，此时M2恰好关断，那么M2的Vgs=VTH。M1的电流为ISS，根据电流电压公式可以求出M1的Vgs。

在大信号的时候，比如CML，要让电流完整的做切换，此时的Vin要大于上面计算出的临界值，使其不工作在线性区。对于差分对来说，这种应用比较吃力，因为线性区范围比bipolar要广。

半边电路法，当两边完全对称的时候，

如果有电阻的不匹配，那么共模到差模的增益如下图所示。这里考虑了尾电流源的输出阻抗RSS和等效电容CSS。因此，从输共模到差模的增益存在零点。

考虑差模增益，这里考虑了电容CD，所以差模增益存在极点。

所以CMRR存在两个极点，由于RSS比RD大，CSS比CD大，因此第一极点比第二级点要远。

电流源负载的差动对

其很难稳定，因为上面是是电流源，下面也是电流源，很难使这两个电流源保持一致，所以需要共模反馈。

下图的接法也是不正确的，不能保证电流一致。因为不知道尾电流源的Vds和M3M4的Vds

画出半边电路，求频率响应。

主极点在M1的栅极，CGD经过密勒等效可以求出主极点。

次级点在输出节点，该次级点由于输出阻抗比较大的缘故，因此也不会在很高频的地方，所以也不容忽视。

有源电流镜

自偏置，所有管子工作在饱和区，不需要共模反馈使其稳定。

有源电流镜不是完全对称的结构，因此不能使用半边电路法分析其增益。

其GM=gm1

求其输出阻抗，先求从输出看向M2的阻抗，其阻抗就相当于内阻是1/gm1的源极负反馈的输出阻抗，为ro2+1/gm1+gm2*(1/gm1)*ro2≈2ro。

接下去求整个电路的输出阻抗，从输出向下看的输出阻抗是2ro，向上看是rop，向下的电流是i，向上的电流也是i，那么就可以列出方程，求得输出阻抗最终使ron//rop。进一步可得增益。

忽略input，考虑频率响应，考虑Cm和CL两个电容。P点的极点很好计算。

求Cm的零点，要使Vout=0V，那么两个电流镜的电流都只能通过Cm流出来。所以Cm流出来的电流是2i，经过计算，可得零点。

对于CL带来的极点，该极点是电路的主极点。

零点的话，要使vin不管是多少，输出都为0，那么要求CL的阻抗为0。该零点在无限远处。

总的传输函数是：

全差分

需要共模反馈使其正常工作，偏压不能直接给电压，不能使电流源的电流相等。

一个好的电流源包括以下几点：电流是可定义的，是从其他地方复制来的。Rout越大电流源越接近理想。可无限复制。复制电流时电流源的晶体管尺寸不能直接改变W/L，而是改变m，直接复制。

共模增益，差模增益，共模到差模的增益是三个完全不同的概念

实际的尾电流源并不是理想的，输出阻抗是有限的，因此在输入输出曲线上面，在一个MOS管截止后对应的曲线也并不是平的，而是有斜率的。

当M2关断的时候，Vin1继续增加,Vin2继续减小，那么VP点也会增加。所以该电流就会发生变化，变化量是。所以Vout也会跟着变化。这是对于尾电流源是非理想电流源的情况。如果是理想电流源，在一个MOS管关断后，M1的电流就是固定的ISS，因此Vout也是固定的。

当REE趋近于0时，M2关断时，M1增加，其电流和电压是指数关系，因此输出电压也是指数关系。

对于MOS管同理。RSS为有限值时，一端关断之后，存在斜率。

RSS趋近于0时，电压和电流是二次方关系。

电流源

当电路两边不对称，M2的宽长比是M1的2倍，如果共模输入的时候，两个管子的Vgs相等，所以M2的电流是M1的2倍。因此，其gm2也是gm1的两倍。当给M1一个的小信号，给M2一个的小信号。那么M1的，M2的。那么,

当输入一个是NMOS，一个是PMOS时，由于MN电流固定，所以vo1固定，由于MP电流固定，所以Vgs固定，因此。所以总的增益为1/2。

求增益

MOS电流镜栅极电压几乎都相等。

bipolar电流镜基极电压不相等，并且每个管子的VBE只要有一点差别，就会导致电流有很大差别，因此需要电阻，这样可以使bipolar电流镜有更好的匹配。

bipolar的输出电压最低要在1.2V以上，是一个比较高的值。而CMOS具有更宽的输出摆幅。为了使输出摆幅范围比较大，加入电阻使其栅极比漏极电压高，这样可以使四个管子工作在饱和区的边缘，并且具有与较大的摆幅。

做一个电流很小的电流源

如果用简单电流镜的话，要使电阻非常大才能使电流非常小，电阻非常大的话其阻值很难控制。

那么就可以用wilder电流源，把很大一部分电压都被RE给吃掉，所以VBE比较小，所以电流也比较小。

当做一个电流镜时，栅极都是高阻抗，所以栅极电压基本上都是一样的，但是地电压，每个MOS的源极流到PAD的距离是不一样的，所以这段距离会有阻抗，这就导致离PAD较远的MOS管的Vgs没有离PAD较近的MOS管的Vgs大。

影响电流源电流精确的因素有宽长比和阈值电压两个因素。

对其求偏微分再归一化，可以看到两个值是如何影响电流的匹配性的。

对其求平方项更直观，这里省去了两项的乘积，因此△是一个很小的值，两个很小的值的乘积更小，趋近于0，忽略不计。

根据关系式，要想让电流源的匹配性越好，那么需要宽长比越大越好，过驱动电压越大越好。注意，这只是针对电流镜的失配而言。对于差动对的输入对管，不是这种方法减小失配。

CMRR和输入失调

假设电阻有失配，MOS管有失配，尾电流源非理想，即输出阻抗有限。

共模到差模的增益需要越小越好，因为当输入相同的时候，理想的输出也应该是相同的，Vout=0。但是由于不匹配导致输出相同的时候，输出并不为0，这个增益使不想要的，所以希望其越小越好。

下面求由于RC导致的共模到差模的增益和由

CMRR是：要的gain/不要的gain=差模增益/共模到差模的增益，所以CMRR要越大越好。分别求电阻失配和MOS管失配的。由于两个是互相独立的，因此用平方表示最终的。

将运放中所有的失配导致的失调提取出来放在运放最前面表示为Vos。然后将运放看成完全对称的。将输入短路，找到Vout的大小，用Vout平方/增益平方就是Vos。

反馈

基本概念及特性

负反馈是为了稳定，例如运放。

正反馈为了不稳定，振荡器。

增益

闭环增益将开环增益缩小了1+Aβ倍。

带宽

如果原来的开环系统是单级点系统，那么闭环系统也是单级点系统，并且，开环和闭环的增益带宽积保持不变。因此可以牺牲增益来换带宽。

输入输出阻抗

反馈还可以改变输入输出阻抗。这与反馈类型有关，一般有四种组态。

电压输入组态，需要将电压反馈回来与原来的输入电压做减法之后再输入给运放。所以是串联，那么闭环输入电压变大了1+Aβ倍。

电流输入组态，需要将电流反馈回来做减法后再输入给运放，那么就是并联状态，所以闭环输入阻抗就是开环输入阻抗的1/(1+Aβ)。

电压输出组态，需要将电压复制，因此是并联。所以闭环输出阻抗是开环的1/(1+Aβ)。

电流输出组态，需要将电流复制，因此是串联，所以闭环输出阻抗是开环的1+Aβ倍。

下图是电压-电压反馈。

求输入电阻，将输出电压看成是理想的，所以输出电阻为0，将输入信号看成测试信号，求得输入电阻。

求输出电阻。

将输入电阻看成理想的，所以输入电阻无穷大。然后将输出看做测试信号，求得输出电阻。

线性度

假设运放的放大倍数有二次谐波。那么输出之后的二阶谐波/基波的比值=b1和a1的比值如下式

加入反馈之后，二阶谐波/基波的比值为下图所示，这个值比开环小了,即线性度变好了，变好了倍。

噪声

反馈不能抑制噪声

下图是噪声的计算方式，一般是将输入关闭之后，测得输出噪声，用输出噪声平方/增益平方就是输入噪声。

下图中，第一幅图是开环的噪声的输出对应开环输入的情况

第二幅图是闭环输入噪声对应输出的情况。

两幅图得到的最终的输出噪声应该是一样的，所以最终的处结果，开环输入噪声=闭环输入噪声。

所以反馈并不能改变噪声大小。

四种反馈组态

下图都是常见的反馈网络

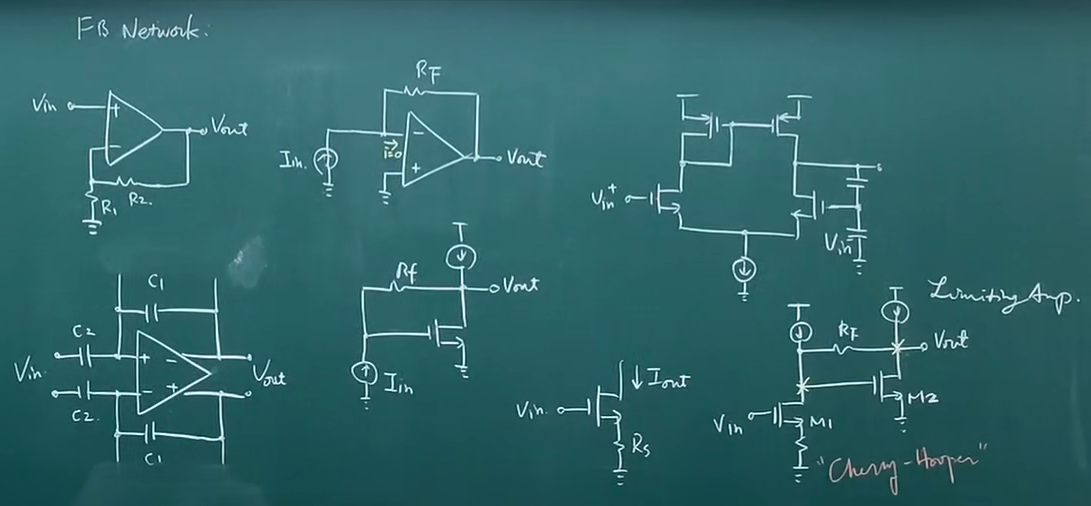
如何给这个全差分画版图，不能按照它原理图的折中画法画，因为中间走线必然不能对称。

应该将尾电流一分为二排在最中间，然后两个运放分别排在尾电流源的上面和下面，依次画其他器件。这样能够保证电路完全对称。并且可以使该模块与下一个模块之间的走线最小。还可以使电源线均匀的分布，减少IR drop。

电压-电压反馈

反馈分析，G模型

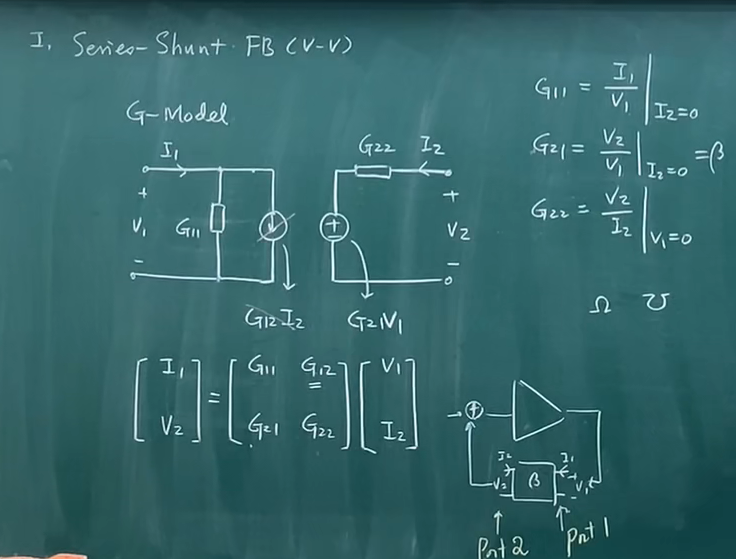
分析步骤

求出G11,G21,G22

将环路打开，此时包含负载。

写出开环增益

写出传输函数

写出输入输出阻抗。

应用到下面这个例子中，就可以得到精确度比较高的增益。

电流-电压反馈

Z模型

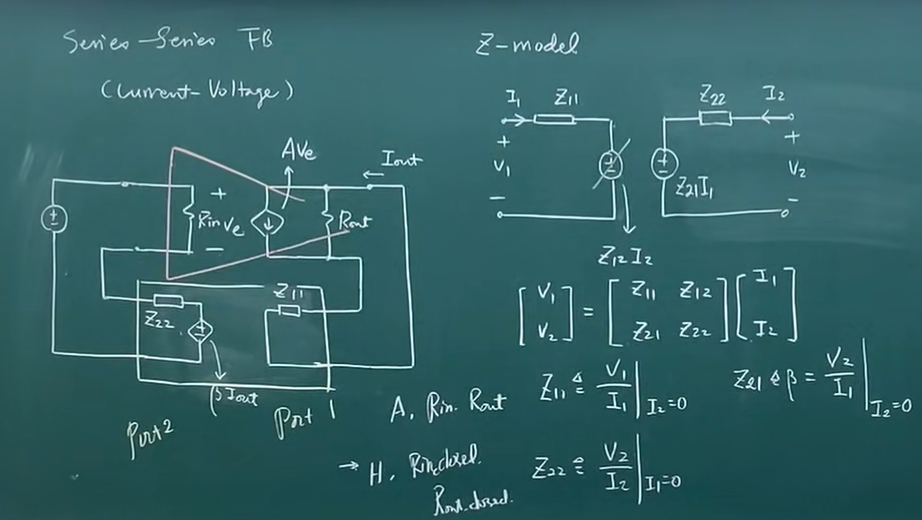
输入阻抗无穷大，输出阻抗=(1/gm3)//Z22

电压-电流反馈

Y模型

电流-电流反馈

H模型

运放

输入阻抗无穷大，输出阻抗无穷小，高增益。频率补偿。

GBW，共模输入，DC输出，压摆率。功耗。电源电压。CMRR，PSRR。

共源共栅运放

套筒式运放，使每个管子都在饱和区，并且把cascode管子压到饱和区边缘。需要合理设置偏压，并且需要共模反馈来保证上面的电流源相加恰好等于尾电流源。

由于上面两个管子消耗2个过驱动电压。下面消耗3个过驱动电压，那么留给VOUT的变化量会非常小，因此，如何偏置是非常重要的，要使所有管子都工作在饱和区边缘，并且VOUT的输出范围最大。

该远方如果接成单位增益负反馈形式，求其输出摆幅，可以得到其输出摆幅是非常小的。

所以该运放有几个特点，高速，低压，输出摆幅小，输入共模小。

下图由于打叉的位置看进去的阻抗是1/gm，因此该极点在很高频的地方。所以不用考虑。需要考虑的就是输出极点。

折叠式共源共栅

输出摆幅VDD-4Vod，摆幅比上面的共源共栅摆幅大一点。

输入最高可到VDD，最低到Vod+Vgs1。所以输入范围是比较大的，并且增益也很高。

它也需要共模反馈。增益可达60dB。

如果再加pmos输入对，可达到轨对轨输入。

当两个输入对同时工作时，GM是两个输入对的gm相加。当一个输入对工作的时候，Gm是一个gm。

下面这个电路，只有输出节点是高阻抗，所以输出极点才是需要考虑的，其他节点都是低阻抗不需要考虑。

Gain Boost OPA

负反馈

输出电阻被放大了（1+A）倍

在共源共栅运放里面应用Gain Boost方法，提高增益，但是四个运放功耗太大。

将两个运放合并，用一个差动的运放，也可以实现。

思考内部运放如何做。这里为了简便，只考虑下面一半的运放如何做，上面一半类似。

如果内部运放这样接，那么对于M3来说，VX-VY是其Vgs。对于M5来说，VX-VY＜|VTH|。那么联立起来就是VGS＜VTH，那么M3管子无法导通。这种做法不行。

如果用NMOS作为内部运放的话，Y点本来需要压到很低=1个Vod。那么对于NMOS输入对来说，1个Vod需要大于NMOS的Vgs+尾电流源的Vod。这不可能实现。所以NMOS输入对的方法也是不行的。

如果内部运放用折叠式输入，那么就可以保证M3工作在饱和区。

对于M5来说，VX可以比VP高VTH，对于折叠输入来说，VY比VX高Vod。

所以VY-VX＞Vod+VTH。对于M3来说，VY-VX就是VGS3。足够M3导通了。

该电路也需要共模反馈。内部运放需要共模反馈，外部也需要共模反馈。

求该电路增益。

下面一半输出阻抗是

上下并联就是

A是内部运放的增益，折叠式也是

所以整体增益可达到的量级。

两级运放

增益可到100-120dB。

好处：第一级的输出摆幅不用很大，因为小信号会经过第二级放大后摆幅会增大。

输出摆幅增大。

频率响应

第二级输出极点，电容很大，电阻很小

第一级输出极点，电容很小，电阻很大。

所以 极点的大小差不多，有可能会引起不稳定。需要频率补偿。

在第二级输入和输出之间，加密勒补偿。

该电路输入，需要大于Vgs+Vod。小于VB1-Vgs+VTH。

对于单端输出的两级运放。这个电路有一个好处，可以使M6和M4流过的电流相等，即M7电流为M5电流的一半。如果M6尺寸和M4一样。那么经过电流电压二次方的关系。M6的Vgs跟M4的Vgs差不多。可以达到比较稳定的平衡。

共模反馈

上面有电流源，做不到让DC工作点正好与该电流源大小值一样。

如果下面的输入管也用电流源接进来。经过一个电阻该输入管的栅极电压才能动，否则电阻锁死。

由于左边支路Vgs=Vds。而右边支路Vgs不一定等于Vds。那么右边支路如果哪个电流源比较弱，就会将输出电压抬高或抬低。那么就会将强的那个管子进入线性区。从而也变弱，让输出电压反方向变化。最终达到balance。但是该法导致管子进入线性区，因此也不行。

有效方法就是自偏置。将输出和输入锁定，两个管子都工作在饱和区。

不能保证I1+I2=I3，会导致管子进入线性区。一旦进入线性区，增益就飘了。

加共模反馈，使输出保持在VDD/2附近。如果输出电压过高或者过低，就由共模反馈模块调节尾电流源把输出电压拉回来。要保证所有管子都工作在饱和区。

所以对共模反馈的要求：

1、能测量输出共模电压

2、能跟参考电压相比较

3、能调节

首先用两个大电阻检测输出共模电压，大电阻不会影响该节点本身的输出电阻，因此不会影响增益。跟参考电压比较，调节尾电流源。

为了减少尾电流源的剧烈扰动。可以设置0.8ISS的尾电流源固定，留0.2ISS给可调节的尾电流源。

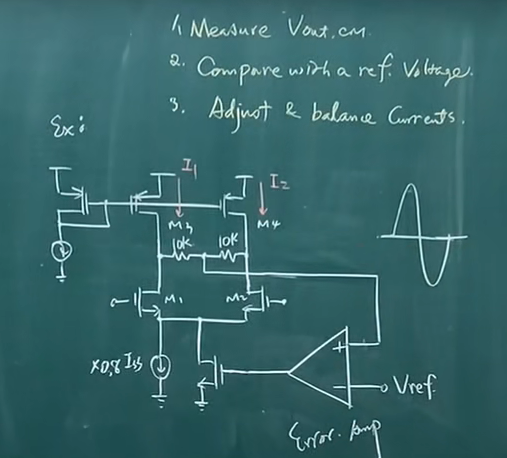
根据电流电压公式可以求出M3和M4的ro。反馈调节就是通过该ro上的压降体现出来的。

假设M5栅极有△V扰动，那么尾电流就会有gm5?*△V的变化。该电流在ro3//ro4上的电压变化就是输出电压的变化量。所以输出共模电压变化量就是gm5 *?△V*ro/2。经过A放大之后回到M5栅极，所以可以求出环路增益远远大于1，因此可稳定。

共模反馈电路，用两个工作在深线性区的MOS管。

反馈的电阻的阻值跟共模输出电压成反比。

当共模输出电压太高时，反馈电阻变小，导致M5电流增加，使输出电压降低。反之同理。

可以做到M3和M4流过的电流之和永远等于M5的电流。

该电路尾电流源的偏置可以使用相同的电阻模拟M6和M7的作用。

使电流镜成比例系数，电阻也成比例系数。

什么电路需要共模反馈？

压摆率

RC滤波器输入阶跃响应，输出会一段时间后跟随输入。并且斜率一直在变。

实际上，对于一个运放来说，充电的斜率与电流大小有关，求导之后可以看到斜率是定值，那么就说明输出随输入的响应斜率是不变的。

所以稳定的时间与压摆率有关。

两级运放要给密勒电容充电。假设两级运放接成单位增益负反馈。

如果Vin阶跃信号，那么ISS都流过M1，所以ISS要对Cc充电。

假设10级运放。，输入小信号，输出有很大的电容。

输入信号经过9级运放已经饱和了，变成大信号。

对电容充电，假设M2关闭，所有电流流过M1，但是电流源偏置只能提供ISS/2的电流，那么就需要电容CL再提供给M1 ISS/2的电流。M2管上面的电流源的ISS/2的电流也流过另一个CL。所以单边的压摆率都是ISS/2CL。一边降低，一边升高，所以整体的压摆率是ISS/CL。

大压摆率示例：

该电路Q2发射极比输入低一个VTH-IR，基极比输入低两个VTH，所以在dc的时候Q1和Q2的基极-发射极电压比较小。

简化电路，当Vin+有的上升的时候，Vin-下降时。Q1基极也会有变化，Q2基极也会有变化。并且Q1发射极下降，Q2发射极。

对于Q1来说，VBE减小，Q1关断。Q2VBE增大，电流增大。该电流对CL充电。所以SR是一个正比于的值。这跟简单差动对就不一样了，简单差动对的SR是定值。这与RC滤波器所期望的结果是一样的，RC滤波器的SR与A0有关。

求该电路的小信号，左边支路电流减小了，有边之旅电流增加了，所以总的输出电流增加了。输入vin是。所以可以求出Gm。

求输出电阻，输出电阻最终结果如上图所示。

稳定性

本章讲的是运放的稳定性

稳定性判断方法

一、稳定和振荡的必要条件。

二、零极点

对于一个稳定的系统，所有的极点都得是左半平面的极点（要么是左半平面的实极点，要么是左半平面的共轭极点）。如果右半平面出现共轭极点，那么经过一段时间的振荡之后，这两个共轭极点会跑到虚轴上去。就会变成振幅是的振荡器。

假设一个传输函数有两个共轭极点。做拉普拉斯变换之后，在关系式中，如果a＞0，那么就会振幅就会越来越大，如果a=0时，振幅保持不变的振荡器。如果a＜0，那么振幅会越来越小最终稳定。这也就是为什么稳定系统需要a＜0，即极点在左半平面。

三、波特图

看反馈回来的量的幅值变化情况，所以纵坐标轴是，如果那么相当于输出全部反馈的输入，此时的是最糟糕情况下的波特图。如果的时候都能稳定，那么是其他值的时候也会稳定。

相位裕度低于45度的时候响应会有振铃。

四、奈奎斯特图

将画成极坐标的形式，画出海螺形状的图。如果到180的时候在（-1,0）右边，稳定。在（-1,0）左边，不稳定。

反馈对单级点系统的影响

反馈对双级点系统的影响

双极点在反馈系统里面变成一对共轭极点。在很小很小的时候，这两个极点在实轴上，当逐渐增大的时候，这两个实极点会相向而行，相遇之后又在虚平面上背向而行。共轭极点离原点越近越稳定，离原点越远越不稳定。因为是实轴平方*虚轴平方。越大，共轭极点离实轴越远，越不稳定。

将共轭极点的传输函数写出来，并写出和Q的值。越大，Q值越大越不稳定。从图中也可以看出，Q=1的时候有过冲，Q=0.7的时候没有过冲。

频率补偿-极点分裂

当在单位增益带宽内出现两个极点时，相位裕度可能所剩无几，不稳定。

所以寻找方法：添加极点、将第一个极点往里推、将第二个极点往外推、极点分裂，一个往里一个往外。前三种方法都不可行。最后一种方法是可行的。就是在第二级输入和输出之间加密勒电容。（注意，输入与输出之间极性反向）

对上图做小信号等效图，求传递函数。

用主极点近似，求两个极点，并与添加密勒电容之前的极点比较。

主极点变小了，次级点变大了。满足要求。

但是密勒电容创造出来一个零点。该零点是右半平面的零点，并且位于主极点和次级点之间。对稳定性有致命性影响。

对于两级运放来说，也是同样的。右半平面的零点导致相位裕度为负。

如何使两级运放保持稳定？

法一：当C1<<C2时，简化极点。如果此时能使零点和次级点在GBW以外。那么就可以稳定。

该方法的具体推导如下。

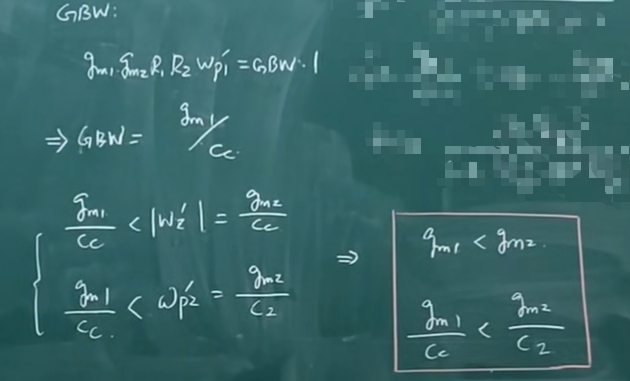
则最终推导出来的结果就是要满足下述条件才可以。

法二：移除零点。引入电阻。

求零点，无论输入是什么，输出都是0。

如何选择电阻的值。

（1）使零点在无穷远处。

（2）使零点与次级点抵消。

PSRR

与CMRR定义方法一样，要的东西/不要的东西。越大越好。

求两级运放PSRR。

首先看第一级运放。VDD变化的时候，由于理想电流源的作用，不会对输入对管的源极造成影响。因此VDD不会影响输出。VSS变化的时候，由于M3/M4管子的电流镜，饱和区时，输出电压被锁定，因此VSS也不会影响输出。

第二级运放，VDD变化的时候，由于电流镜的作用，Vb会跟着变化M7的栅源电压不会变化，因此对输出没有影响。VSS变化的时候，由于M6管子的栅极电压是被锁定的，因此会导致M6管子的栅源电压发生变化，进而影响输出。画出小信号模型计算VSS对输出的影响即可计算出PSRR-

输出级

输出级用于驱动芯片外部。

Class A

下图电路中，Q2是偏置，永远提供Ib的电流。当Vin升高的时候，Q1产生的电流一部分流过RL。导致Vout也会随着升高。直到Q1进入饱和区，Vout=VCC-Vsat。当Vin反向增大时，Vout也会减小，Ic1逐渐减小，Vout反向增大，由RL电流和IC1电路相加=Ib。直到Q1进入饱和区。

如果负载电阻RL比较小，那么Iout会比较大很快电流Ib全部由Iout提供。此时Vout=-IbRL。

画出上图的电压电流随时间变化曲线。求效率=25%。这个效率是不好的，因为一直有直流，能提供给输出的太少了。

Class B

Q1和Q2只有一个工作。

Vin大于0.7或者小于0.7时，输出才会工作。因此，输入输出会有失真。

效率可以达到78.5%

Class AB

为了解决Class B的失真问题。

如果加两个0.6V的二极管。需要给二极管之路一个小电流。要让直流的时候，没有电流流过，0.7V管子就导通了，就有直流电流了，所以这个要选择电流源让管子处于导通边界。

上述电路的输入输出曲线如下图所示。会有offset，不是经过原点的曲线。

两个二极管可以用下述方式产生。

下图电路可以解决上述电路的offset，两个电路起短路保护作用。

下图是经典的CLASS AB的输出级电路。

两个电阻和Q3,Q4起保护作用，当Q1的电路很大时，电阻会有600.V的电压，导致Q3导通，将Q1基极电流流走，导致Q1基极电流下降。起到保护Q1的作用。

当Q2电流比较大时，Q4,Q5,Q6导通，反馈回第一级输出。保护Q2。

达林顿管

下图是经典的电路，涵盖了很多运放只是

第一级运放，差分输入，单端输出。源极负反馈电阻，Q5,Q6匹配性更好。

第二级运放，密勒电容。

输出级，Class AB。达林顿管。短路保护。二极管解决失真。

自偏置，Q10，输入经过3个VBE到VCC。

DC时，输入为0V。输出为VDD/2。

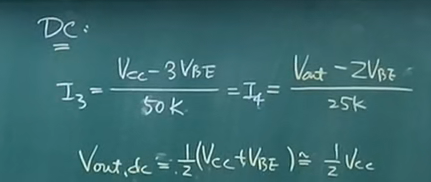
第一级运放，小信号。Q1的栅极变化多少直接就给到Q3的栅极。所以小信号省略Q1,Q2。ro4//ro6的提供两倍的电流，因此可以求出第一级增益。

整体电路经过反馈回第一级电路，反馈至1K电阻的中心位置，所以是0.5K电阻。整个电阻的增益是51.

应用

运算放大器