改进的A*算法的路径规划(3)
5.4实验结果与讨论
为验证本文算法的有效性,在模拟越野环境中完成路径规划,并通过仿真对比?实验验证了本文改进算法的可行性和综合性能的优越性。
5.4.1?与?传?统A*实验对比
为了验证改进A*?算法与传统A*?的优越性,建立了70×50的栅格地图(并不是?越野地图,因为传统?A*算法不适用于越野栅格地图),传统?A*?算法本文也设置为?16邻域节点选择,设置单位栅格长度cell?=1m,??步长?k=2,?原自适应评估函数则变?为。
![]()
同时为了量化算法性能,本文设定了评定函数P,P?设定为智能车辆按算法规?划的路径进行移动所需要的时间,具体为:
式中:1为路径长度,?v?为智能车速度,本文假设1m/s,N? ???为路径拐点数,θ为转角和。
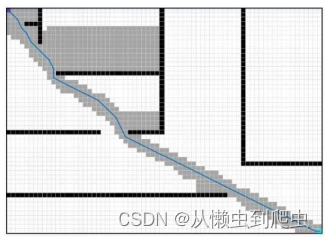
?(a)传统A*算法规划的路径
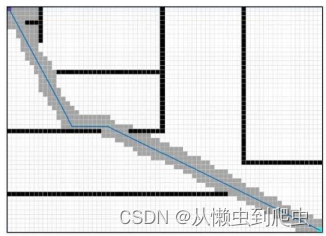
(b)改进A*算法规划的路径
图5-14传统?A*算法与改进A*算法比较
表?5?-?3?路?径?规?划?算?法?对?比
| 比较参数 | 传统A*算法 | 改进A*算法 |
| 节点数/个 | 597 | 416 |
| 路径长度/m | 110.46 | 98.77 |
| 转角和/度 | 247.6 | 90 |
| 拐点数/个 | 11 | 2 |
| 评定函数P/s | 126.96 | 102.86 |
通过观察图5-14,可以明显的看出改进的A*?算法规划的路径更为平滑,由于?引入了方向变化惩罚,使得规划的路径只有2个拐点,而传统A*?却有11个拐点。 通过表5-3可看出,改进的A*算法基本各个方面均优于传统A*, ?在算法效率上提?高了30%,尤其在拐点数上减少了5倍。实验表明改进 A*?算法灵活性更高,能依据环境信息的不同,有效改变搜索空间,获得全局上的最优路径。
map2d=Array2D(w,h)
for x in range(4,20):
for y in range(0,13):
map2d[x][y]=1
for x in range(0,18):
for y in range(16,20):
map2d[x][y]=1
for x in range(25,30):
for y in range(5,20):
map2d[x][y]=1
"""
"""
#设置障碍(地图二) 5.4.2?越野环境路径规划对比
为了验证本文所提算法在越野环境下的性能,建立70×50的越野栅格地图,并?将规划出结果与传统 A*?算法(传统 A*?算法在越野环境只考虑障碍物),APF?算法?(假设在越野栅格地图值大于0.7的栅格为障碍物)进行对比。图5-15(c)和图?5-15(d)?分别为改进 A*算法在不同环境威胁敏感度ε规划的路径。当越野智能车辆越野性?能较差、防碰撞能力较差时,可选择威胁敏感度ε=2,如图5-15(d)所示规划的路?径能够避开障碍物、通过性差的路面和有效威胁区域,安全的到达终点;但如果越?野车辆具有较好的越野性能,可选择威胁敏感度ε=1,此时规划的路径如图5-15(c)?所示,能过穿越沙地通过性差的路面,安全的避开有效威胁区到达终点。
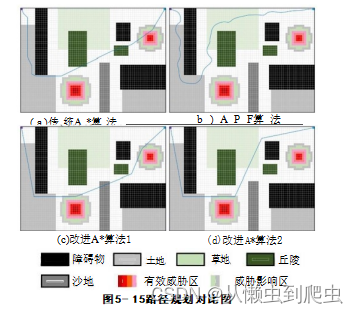
?
图5-15(a)和图5-15(b)分别为传统?A*?算法和?APF 算法所规划的路径,它们规?划的路径均能避开障碍物到达终点,但是与改进A*?相比,本文方法具有以下优势:?1)通过对越野环境建模,能够识别环境威胁和不同道路,能够避免智能车辆从有效?威胁区和通过性差的路面中通过,造成安全风险。2)引入了方向变化惩罚,使得规?划的路径具有拐点少、路径平滑和转弯角度小的优点。3)根据环境位置信息,自适?应调整算法搜索范围,提高算法效率。4)能够通过智能车辆特性,根据取不同的威胁敏感度ε来进行个性化路径规划。
表5?-?4越野环境路径规划算法对比
| 路径算法 | 路径长度 | 拐点数 | 运行时间 | 路径平滑 | 规避障碍 | 规避威胁 | 道路选择 |
| 改进A*1 | 165.7 | 4 | 1.81 | √ | V | √ | √ |
| 改进A*2 | 171.1 | 3 | 1.98 | √ | V | √ | √ |
| 传统A* | 160.8 | 10 | 1.41 | × | √ | × | × |
| APF | 182.3 | 19 | 1.37 | × | √ | V | X |
改进?A*算法与其余算法性能指标对比如表5-4 所示。由表5-4可知,改进的?算法考虑多种越野环境因素影响,因而规划时间略长,但是结合局部区域复杂度惩?罚,只比传统?A*算法少0.4s?。规划路径时要避开威胁要素的影响和通过性差的区?域,所以规划的路径距离略远,但智能车辆行驶的安全性高,生成的路径更为平滑,因此其综合性能较优。
#地图五
for x in range(15,20):
for y in range(0,13):
map2d[x][y]=1
for x in range(0,18):
for y in range(16,20):
map2d[x][y]=1
for x in range(25,30):
for y in range(5,20):
map2d[x][y]=1
for x in range(6,20):
for y in range(6,7):
map2d[x][y]=1
for x in range(8,10):
for y in range(11,18):
map2d[x][y]=1
for x in range(0,8):
for y in range(3,4):
map2d[x][y]=1 为了进一步验证所提算法的有效性,建立尺寸为50×50和30×80的越野地图?A?和越野地图B, ?并测试在不同威胁敏感度ε规划路径的特点,所得结果如图5-16和图5-17所示。
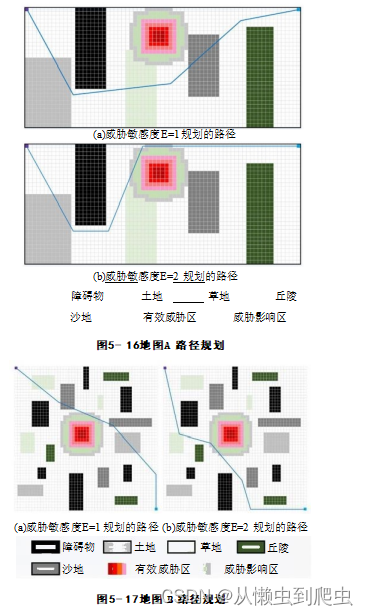
5.5?本章小节
本节针对越野场景路径规划问题,采用栅格法建立障碍物、威胁物和越野道路?模型,模拟真实的越野环境场景。引入方向变化惩罚和局部区域复杂度惩罚来优化?A*算法,使算法规划出的路径更平滑,算法效率更高效。采用改进?Floyd 算法对路?径进行双向平滑,并且进行了防碰撞处理,来确保规划出路径的安全可靠性。仿真?结果表明,所改进的A*算法与传统算法相比较,效率提高了30%,拐点数减少了?4倍,所提算法能够在越野环境多重因素综合影响以及不同车辆性能和任务的要求下快速的规划出安全的路径?。
第六章?总结与展望
6.1?总结
基于视觉的无人驾驶系统在实际复杂场景中存在光照、阴影、道路种类和其他 噪声等问题的影响,使得基于视觉的感知算法在检测精度和效率上仍然存在不足,?例如光照干扰严重影响立体匹配算法精度、背景噪声大大提高道路分割算法的时 间复杂度和不同道路类型要求规划算法具有更好的鲁棒性等。本文以智能车辆的 环境感知技术和路径规划为研究出发点,针对现有的障碍物检测、道路识别和路径规划算法中存在的问题进行了研究,研究结果总结如下:
(1)针对在视差不连续区域、遮挡部分和弱纹理区域,传统局部立体匹配算法?匹配精度低下等问题,提出了一种基于双目立体视觉结构的道路场景三维重建和?障碍物检测算法。首先,针对传统立体匹配算法对光照场景与小物件匹配效果不好?的缺陷,提出了一种基于特征金字结构的卷积神经网络立体匹配算法来计算初始?匹配代价;然后,引入了快速引导图滤波算法实现了代价聚合,减少了计算时间复?杂度;改进动态规划视差值算法用于视差值选取,解决了传统?WTA?视差值选择算?法的视差不连续性问题和传统的动态规划视差值选择计算时间复杂性高的缺陷;?最后左右一致性检测、子像素拟合和唯一性检测等视差求精算法,解决了遮挡与视?差值不连续区域图像的匹配问题。通过对所提的网络进行消融试验,结果证明了所?设计的网络结构拥有更佳的匹配准确度,并拥有更高的运算效率。通过与其他优秀?的算法所进行的定性对比,证明了所提的算法拥有的对光照变化不敏感、运算效率?高和精度高等优点。
#路面分类地图1
for i in range(0,13):
for j in range(20,30):
map2d[i][j]=0.7
for i in range(4,8):
for j in range(15,20):
map2d[i][j]=1.0
for i in range(2,7):
for j in range(0,13):
map2d[i][j]=0.8
for i in range(5,8):
for j in range(0,10):
map2d[i][j]=1.0
for i in range(17,30):
for j in range(0,12):
map2d[i][j]=0.2
for i in range(10,17):
for j in range(10,17):
map2d[i][j]=0.8
(2)针对非结构化场景具有缺乏清晰的道路线和存在复杂的背景干扰等问题, ?提出了一种结合立体视觉的道路消失点检测方法。首先,结合双目视觉技术,实现 ?对路面区域与背景区域的快速估计;其次提出了一系列投票点与候选点的选择规 ?则,以提高检测的准确性与减少计算时长,结合一种有效的投票策略,将在投票空 ?间中获得票数最高的候选点视为消失点;最后,在消失点约束下,融合路面颜色特 ?征、路面区域占比特征和纹理特征,在积分图方法加速下快速准确的分割出道路线。?在?KITTK 数据集下选择各种非结构道路场景上的实验结果表明,消失点检测上与 ?现有的3种方法相比,该方法具有精度高、检测速度快的特点,在道路线分割上与现有的2种方法相比,该方法的精度更高,鲁棒性更好。
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- K8S三台服务器一键部署总结
- SpringBoot-项目引入Redis依赖
- 群狼调研开展某连锁水果店神秘顾客调查
- 【PC电脑windows编写代码-学习uart0串口编写代码-串口程序-简单通讯交互-基础样例学习】
- Vue2+springboot实现三级联动
- Leetcode sql50基础题最后的4题啦
- PyQT5安装配置测试打包教程
- 饥荒Mod 开发(二三):显示物品栏详细信息
- 初识Docker-什么是docker
- 6.1 常见集合和应用