SLAM算法与工程实践——相机篇：传统相机使用（2）
SLAM算法与工程实践系列文章
下面是SLAM算法与工程实践系列文章的总链接，本人发表这个系列的文章链接均收录于此
SLAM算法与工程实践系列文章链接
下面是专栏地址：
SLAM算法与工程实践系列专栏
文章目录
前言
这个系列的文章是分享SLAM相关技术算法的学习和工程实践
SLAM算法与工程实践——相机篇：传统相机使用（2）
相机标定
参考：
标定的方式一般来说是通过拍摄多张标定板的图片，标定板上有一些特殊的图案可以让计算机自动查找到这些图案的位置，根据这些位置可以计算出外参和内参，这是一个畸变和投影方程组求解过程，根据相机镜头方程不一样，至少4-8组标记位可以得到唯一解。
打开Matlab，控制台输入
% 单目相机
cameraCalibrator
% 双目相机
stereoCameraCalibrator
选择左右视图的文件夹，导入图片，我这个标定板一小格为 30 mm
其中一组的左图被遮挡了，不能用
双目标定界面
畸变参数总共有五个，径向畸变3个（ k 1 , k 2 , k 3 k_1,k_2,k_3 k1?,k2?,k3?）和切向畸变2个( p 1 , p 2 p_1,p_2 p1?,p2?)。
径向畸变
x
c
o
r
r
e
c
t
e
d
=
x
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
y
c
o
r
r
e
c
t
e
d
=
y
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
\begin{array}{l}{{x_{\mathrm{corrected}}=x(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6})}}\\{{y_{\mathrm{corrected}}=y(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6})}}\end{array}
xcorrected?=x(1+k1?r2+k2?r4+k3?r6)ycorrected?=y(1+k1?r2+k2?r4+k3?r6)?
切向畸变：
x
c
o
r
r
e
c
t
e
d
=
x
+
[
2
p
1
x
y
+
p
2
(
r
2
+
2
x
2
)
]
y
c
o
r
r
e
c
t
e
d
=
y
+
[
p
1
(
r
2
+
2
y
2
)
+
2
p
2
x
y
]
\begin{aligned}x_{\mathrm{corrected}}&=x+[2p_{1}xy+p_{2}(r^{2}+2x^{2})]\\y_{\mathrm{corrected}}&=y+[p_{1}(r^{2}+2y^{2})+2p_{2}xy]\end{aligned}
xcorrected?ycorrected??=x+[2p1?xy+p2?(r2+2x2)]=y+[p1?(r2+2y2)+2p2?xy]?
以及在OpenCV中的畸变系数的排列（这点一定要注意
k
1
，
k
2
，
p
1
，
p
2
，
k
3
k_1，k_2，p_1，p_2，k_3
k1?，k2?，p1?，p2?，k3?），千万不要以为
k
k
k 是连着的。
D
i
s
t
o
r
t
i
o
n
c
o
e
f
f
i
c
i
e
n
t
s
=
(
k
1
k
2
p
1
p
2
k
3
)
\mathrm{Distortion}_{\mathrm{coefficients}}=(\mathrm{k_{1}}\quad\mathrm{k_{2}}\quad\mathrm{p_{1}}\quad\mathrm{p_{2}}\quad\mathrm{k_{3}})
Distortioncoefficients?=(k1?k2?p1?p2?k3?)
选择畸变参数，calibrate
并且通过实验表明，三个参数的时候由于 k 3 k_3 k3? 所对应的非线性较为剧烈。估计的不好，容易产生极大的扭曲，所以我们在 MATLAB 中选择使用两参数，并且选择错切和桶形畸变。
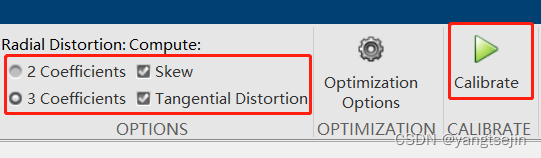
拖拉红线，删除误差大的图像对，使投影误差小于0.1像素最好。然后导出标定参数。
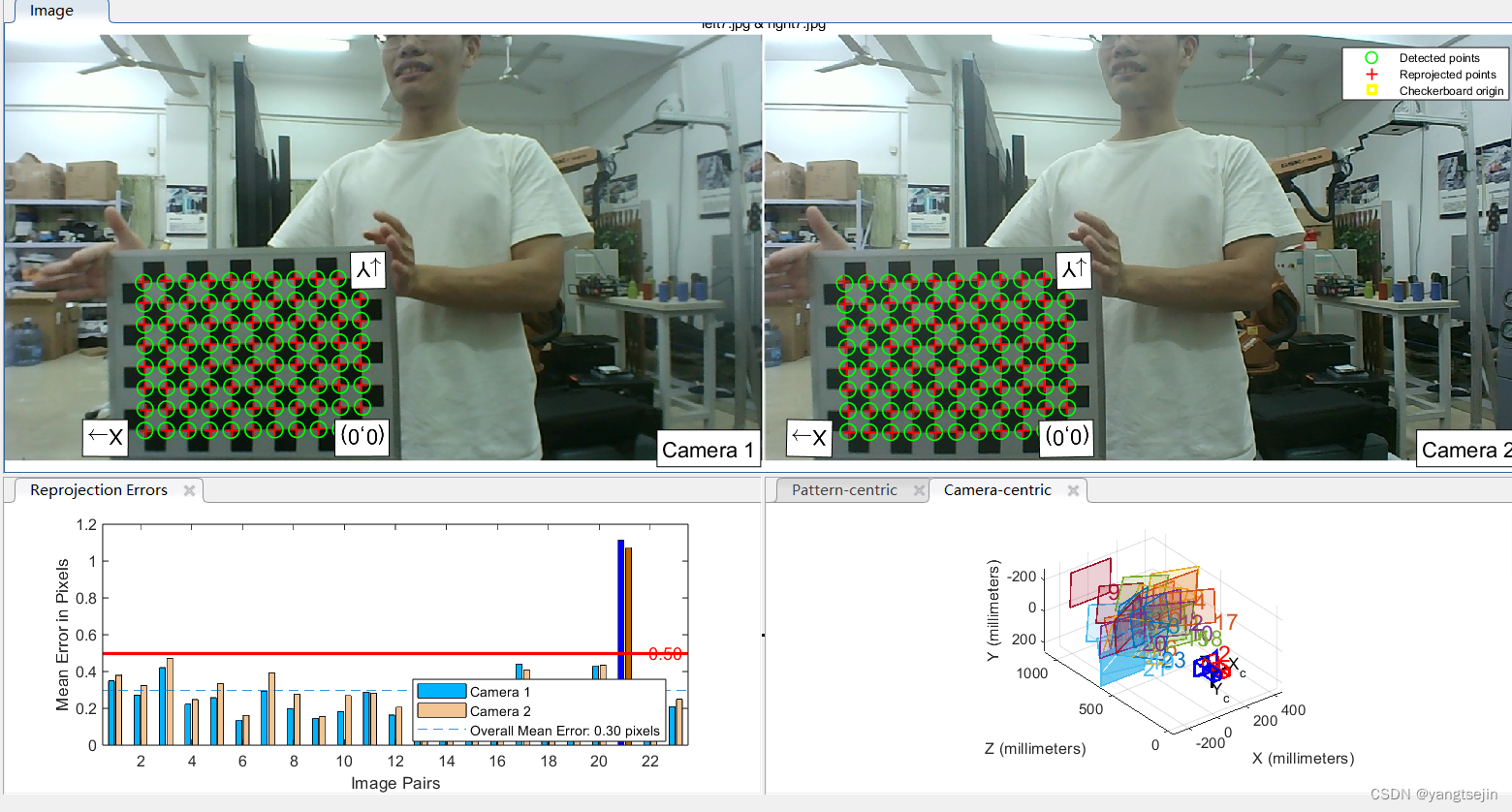
我这里标定的误差在0.4，精度要求高时不能用
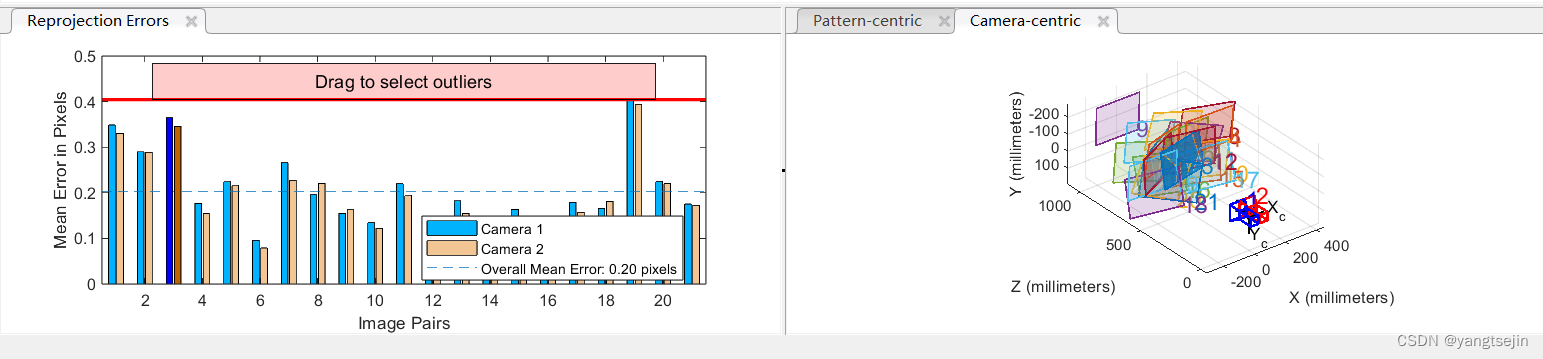
重新拍摄，误差为0.08
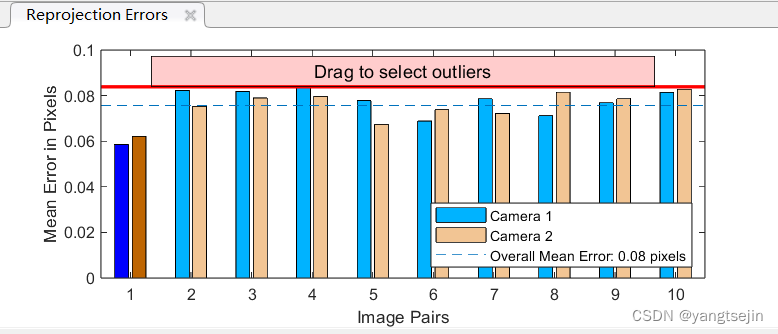
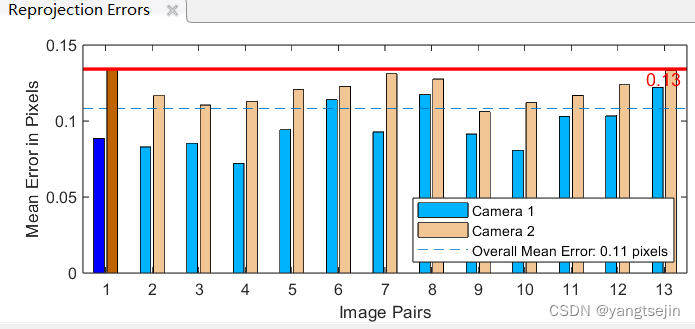
精度要求不高的情况下，0.13的误差也可以接受
可以显示校正后的图像
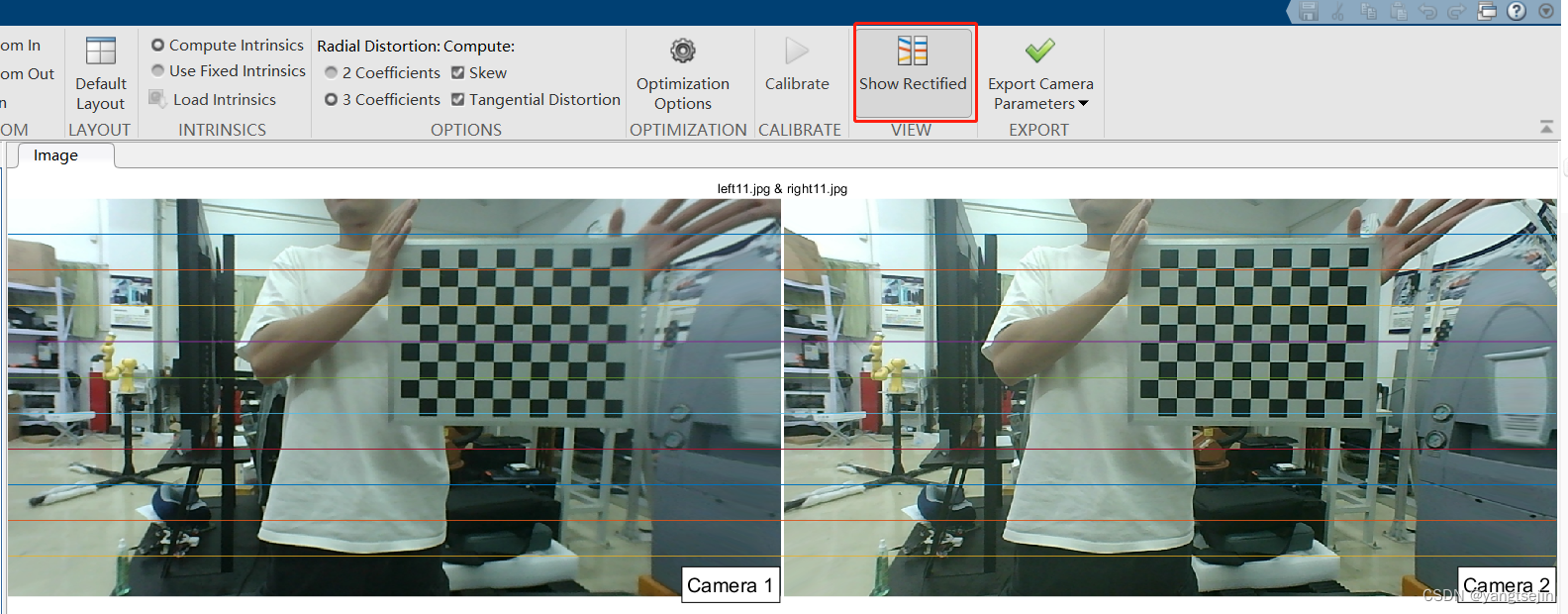
注意：
在Matlab中选择畸变参数时，有时需要选3参数的，有时需要选2参数的，例如我这里选3参数的，图像校正后边缘变形了
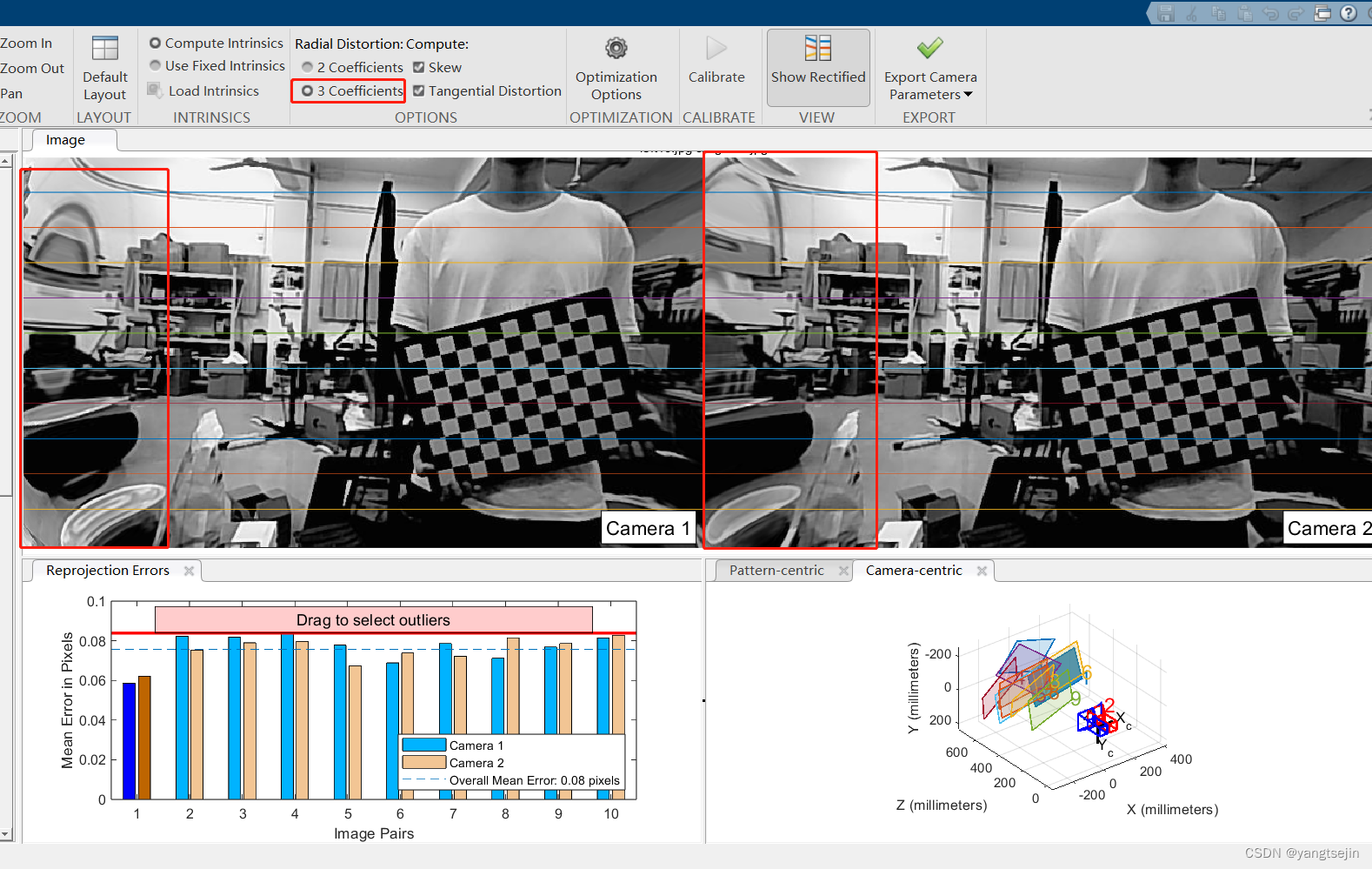
选择2参数，校正后就是正常图像
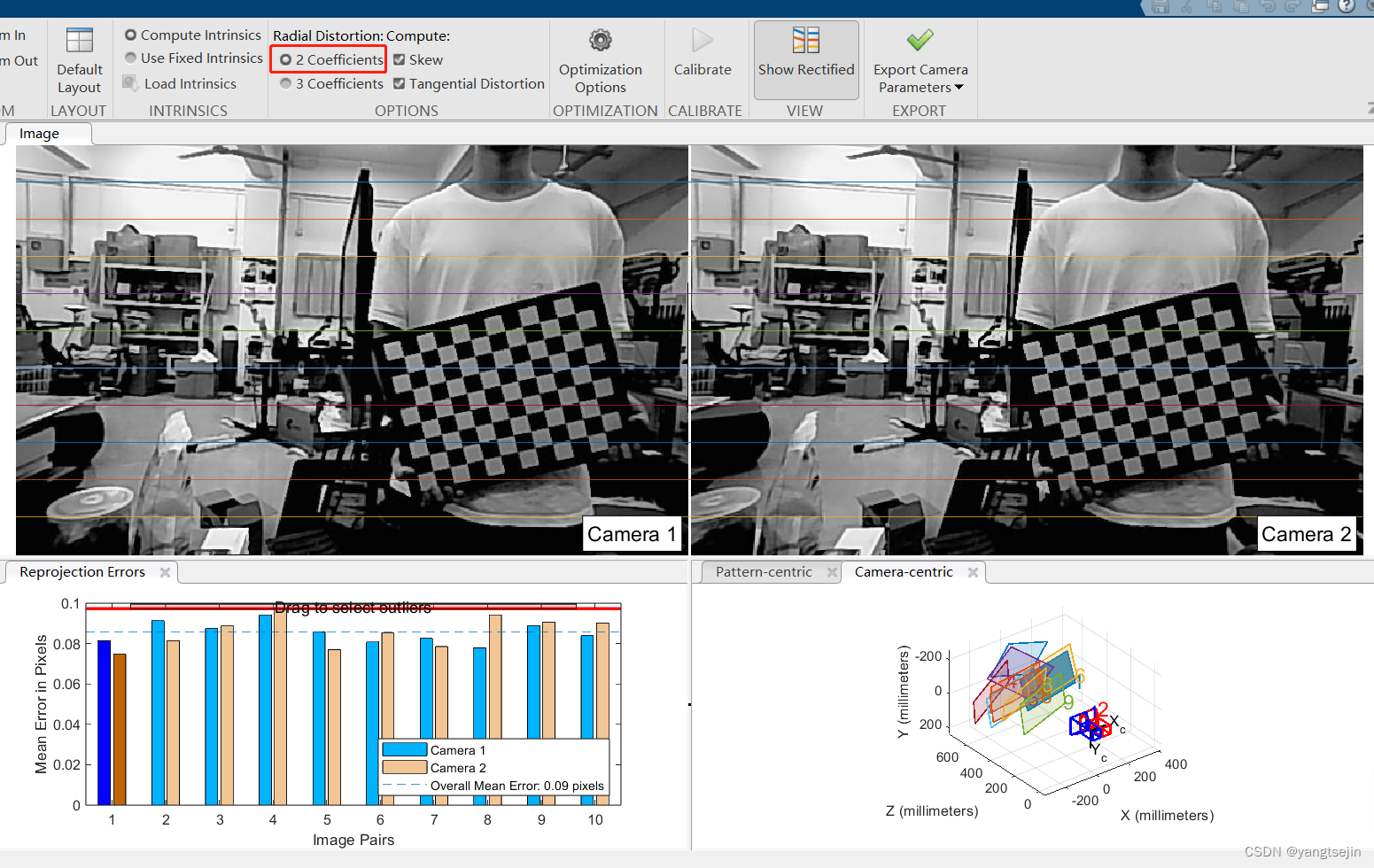
如果选择两参数的模型，那么 k 3 k_3 k3? 的值直接设为0
导出相机参数
误差
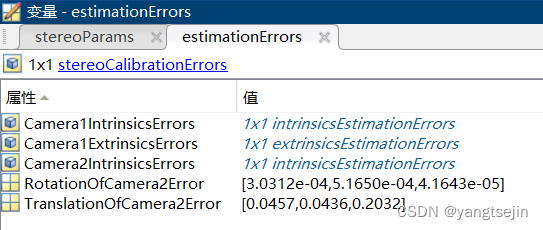
相机参数如下所示
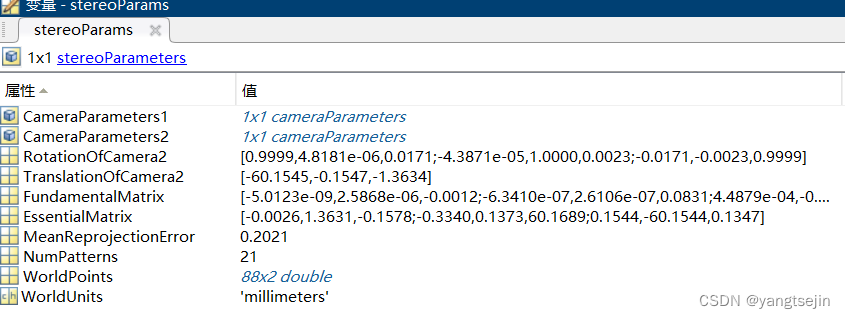
相机外参：
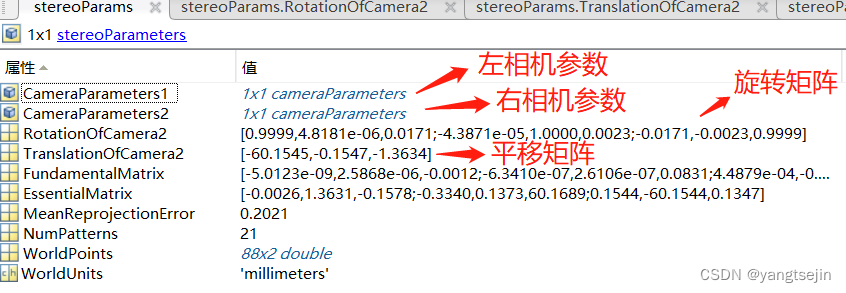
上图中的 RotationOfCamera2 和 TranslationOfCamera2 是右相机相对于左的旋转平移矩阵，即R和T
校正畸变后的图像
相机内参：
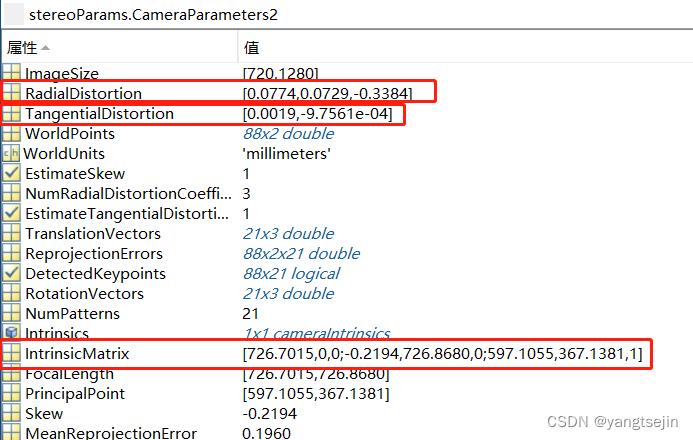
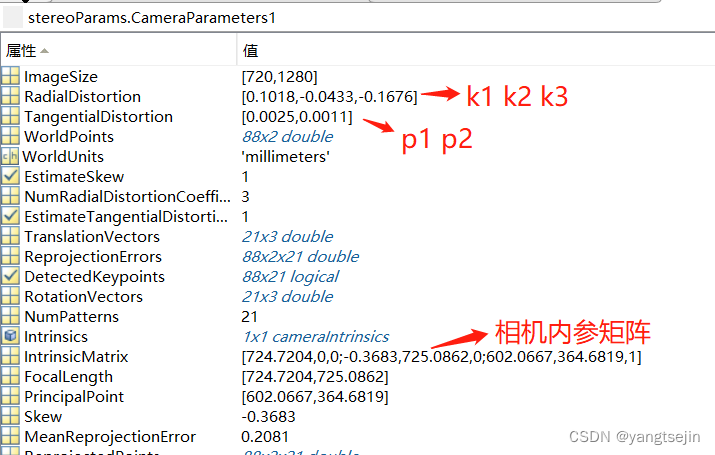
注意：其中畸变系数向量在opencv中的顺序为 k1 k2 d1 d2 k3
opencv中内参的格式为
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
\left[\begin{matrix} f_x&0&c_x\\ 0&f_y&c_y\\ 0&0&1 \end{matrix}\right]
?fx?00?0fy?0?cx?cy?1?
?
填入opencv前的中间处理
-
相机内参和旋转矩阵需要转置后填入
-
k1,k2,p1,p2,,k3按照顺序填入畸变系数矩阵distCoeff -
平移矩阵直接填入
然后将参数写入配置文件中，方便下次读取
图像缩放和裁剪后后参数变化
参考：
缩放Resize与裁剪(Center、Random)Crop对相机内参IntrinsicMatrix的影响
缩放（resize）后参数
内参中的 f x , f y , c x , c y f_x,f_y,c_x,c_y fx?,fy?,cx?,cy? 都会相应的变化
如果图像缩小为原来的一半，那么 f x , f y , c x , c y f_x,f_y,c_x,c_y fx?,fy?,cx?,cy? 都会缩小一半
外参的 R R R 和 T T T 都不会变化
裁剪（crop）后参数
裁剪后， c x , c y c_x,c_y cx?,cy? 会相应的变小
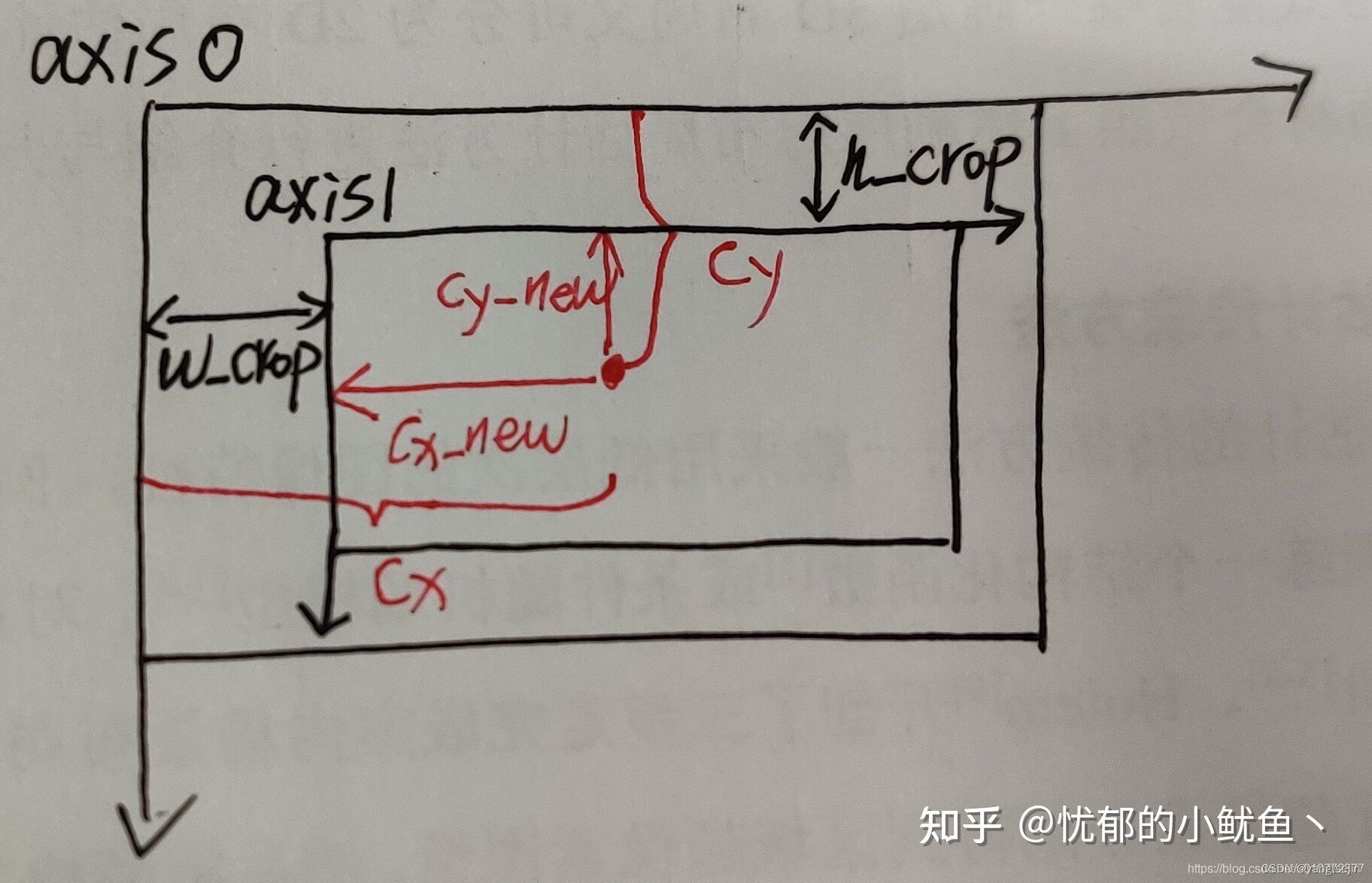
而 f x , f y f_x,f_y fx?,fy? 不变
立体校正
参考：
立体校正的函数说明如下
void stereoRectify(InputArray cameraMatrix1, InputArray distCoeffs1,
InputArray cameraMatrix2,InputArray distCoeffs2,
Size imageSize,
InputArray R, InputArray T,OutputArray R1, OutputArray R2, OutputArray P1,
OutputArray P2, OutputArray Q, int flags=CALIB_ZERO_DISPARITY, double alpha=-1,
Size newImageSize=Size(), Rect* validPixROI1=0, Rect* validPixROI2=0 )
/*
cameraMatrix1-第一个摄像机的摄像机矩阵，即左相机相机内参矩阵，矩阵第三行格式应该为 0 0 1
distCoeffs1-第一个摄像机的畸变向量
cameraMatrix2-第一个摄像机的摄像机矩阵，即右相机相机内参矩阵，矩阵第三行格式应该为 0 0 1
distCoeffs2-第二个摄像机的畸变向量
imageSize-图像大小
R- 相机之间的旋转矩阵，这里R的意义是：相机1通过变换R到达相机2的位姿
T- 左相机到右相机的平移矩阵
R1-输出矩阵，第一个摄像机的校正变换矩阵（旋转变换）
R2-输出矩阵，第二个摄像机的校正变换矩阵（旋转矩阵）
P1-输出矩阵，第一个摄像机在新坐标系下的投影矩阵
P2-输出矩阵，第二个摄像机在想坐标系下的投影矩阵
Q-4*4的深度差异映射矩阵
flags-可选的标志有两种：零或者CV_CALIB_ZERO_DISPARITY ,如果设置 CV_CALIB_ZERO_DISPARITY 的话，
该函数会让两幅校正后的图像的主点有相同的像素坐标。否则该函数会水平或垂直的移动图像，以使得其有用的范围最大
alpha-拉伸参数。如果设置为负或忽略，将不进行拉伸。如果设置为0，那么校正后图像只有有效的部分会被显示（没有黑色的部分），
如果设置为1，那么就会显示整个图像。设置为0-1之间的某个值，其效果也居于两者之间。
newImageSize-校正后的图像分辨率，默认为原分辨率大小。
validPixROI1-可选的输出参数，Rect型数据。其内部的所有像素都有效
validPixROI2-可选的输出参数，Rect型数据。其内部的所有像素都有效
initUndistortRectifyMap()和remap()组合
通过映射的方式逐个找出理想点在有畸变原图的位置。initUndistortRectifyMap()用于产生映射表，remap()用于执行映射。
适用场景：
当要进行多次畸变校正时，使用initUndistortRectifyMap() remap()组合比较有效率，只需要执行一次initUndistortRectifyMap()，后面畸变校正只需要执行remap()即可
用法如下
//计算校正映射矩阵
Mat map11, map12, map21, map22;
initUndistortRectifyMap(cameraMatrixL, distCoeffsL, R1, P1, imageSize, CV_16SC2, map11, map12);
initUndistortRectifyMap(cameraMatrixR, distCoeffsR, R2, P2, imageSize, CV_16SC2, map21, map22);
for (int i = 0; i < imgLs.size(); i++)
{
//进行校正映射
Mat img1r, img2r;
imgLs[i];
remap(imgLs[i], img1r, map11, map12, INTER_LINEAR);
remap(imgRs[i], img2r, map21, map22, INTER_LINEAR);
imwrite("./imgdata/imgleftRec" + to_string(i) + ".png", img1r);
imwrite("./imgdata/imgrightRec" + to_string(i) + ".png", img2r);
//拼接图像
Mat result;
hconcat(img1r, img2r, result);
imshow("校正后结果" + to_string(i), result);
}
undistort()
本质是initUndistortRectifyMap() remap()组合，写在了一个函数里。方便只校正一次。
适用场景：
当只需要执行一次畸变校正时，用undistort()比用组合形式更方便一些。
undistortPoints()
适用场景：
当只需要找出有畸变原图中的少数几个点经过畸变校正后的理想位置时，使用undistortPoints()可达到目的。
组合比较
initUndistortRectifyMap() remap()组合和undistort()结果是一模一样的
initUndistortRectifyMap() remap()组合和undistortPoints()对特征点的校正结果大体一致，在亚像素级别有略微差别
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 软件安全测试报告模版简析，信息安全测评公司有哪些?
- 探寻爬虫世界01：HTML页面结构
- Linux du命令教程：如何有效地管理磁盘空间(附案例详解和注意事项)
- 数字IC后端实现之物理验证Calibre LVS常见错误案例解析
- C++中的继承
- 如何使用固定二级子域名公网访问多个本地Windows Web网站
- H.264运动补偿（Motion Compensation）概念（块匹配、运动矢量和残差编码、块划分和运动估计）（运动估计算法：全搜索、钻石搜索、六边形搜索）
- git format-patch怎么用
- pnpm 源不对 Will retry in 10 seconds. 2 retries left.
- PLC课设实践：三个泵的间隔启动