常微分方程数值解笔记-4

1.线性多步法

龙格库塔法具有较高的精度，但是需要计算多点的导数值，在导数复杂情况下，计算量会很大。因此采用历史信息，即使用若干节点处的y和y'的线性组合来近似y(xn+1)：

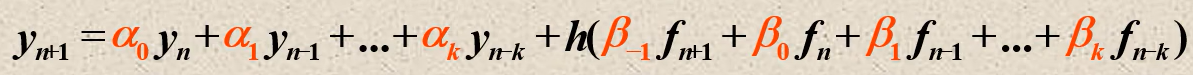
2.基于数值积分的构造法

近似计算右端积分，不同的计算方法对应不同的计算公式

3.显式Adams公式

利用前面节点的导数值即f，构造出外插多项式，从而近似f

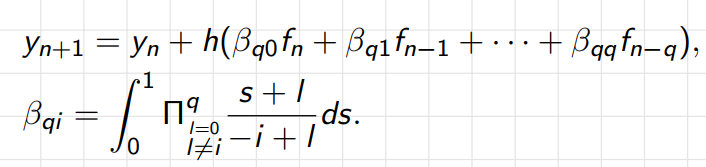
隐式Adams公式则是在公式右侧包含了fn+1项

4.Nystrom公式（等步长）

与Adams区别在于从yn-1开始，积分范围变为-1到1

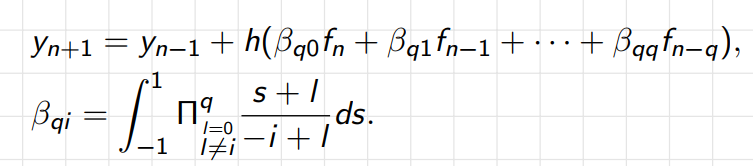
当q=0时，代表中点公式：

5.基于泰勒展开的构造法

首先写出局部截断误差，将精确解和线性多步法的估算解在xn处泰勒展开后，使系数满足局部截断误差的阶次，如果方程不够可以增加约束（设部分为0）

6.线性多步法的收敛性条件

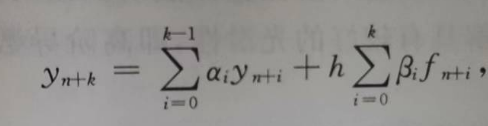
相容且满足根条件则收敛

• 多步法的第一第二特征多项式

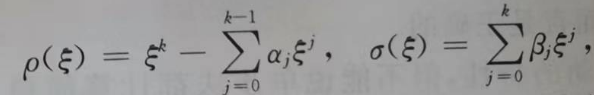
• 与微分方程相容的充分必要条件是ρ(1) = 0，ρ'(1) = σ(1)
• 第一特征多项式的根都在单位圆内或单位圆上，且在单位元上的根都是单根，则多步法满足根条件
• 若多步法是相容的，则多步法收敛的充要条件是满足根条件

截图源自【《数值分析》| 华科 | 研究生基础课】https://www.bilibili.com/video/BV1AK4y1k7Px?p=34&vd_source=a53b34e44cbfd40d72a5b337c3e5a13d