算法训练营Day24(回溯)
发布时间:2023年12月23日
什么问题要用回溯?
暴力都解决不了的问题
组合、排列、切割、子集、棋盘,这些问题
如何理解回溯法?
回溯法比较抽象、困难,采用图形可以帮助理解,解决问题
解决方式:抽象为一个树型结构
模板
void backtarcking(参数(做题的时候慢慢写)){
if(终止条件){
? ? ? ? 收集结果。??????
}
? ? ? ? //单层搜索逻辑
? ? ? ? for(遍历集合的元素集){
? ? ? ? ? ? ? ? 处理节点;//13
? ? ? ? ? ? ? ? 递归操作;
? ? ? ? ? ? ? ? 回溯操作;//1(进行撤销3,方便下次组合成 12)
????????}
}
组合
本题关于剪枝操作是大家要理解的重点,因为后面很多回溯算法解决的题目,都是这个剪枝套路。?
对着?在?回溯算法理论基础?给出的?代码模板,来做本题组合问题,大家就会发现?写回溯算法套路。
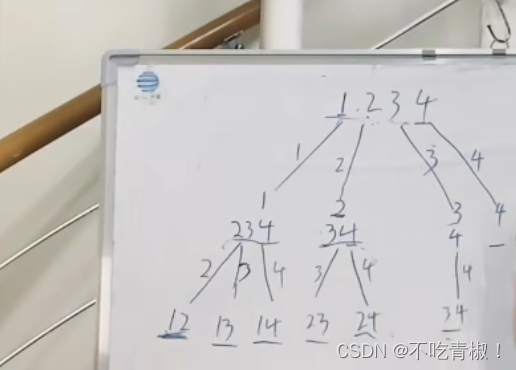
相当于通过递归来代替好多层的for循环
答案:(注意path要回溯,在堆里变化的,要回溯,回溯完之后就都为null了,所以要new一个)
class Solution {
private List<Integer> path = new ArrayList<>();
private List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backingTracking(n,k,1);
return result;
}
void backingTracking(int n,int k,int beginIndex){
if(path.size()==k){
//收割结果
result.add(new ArrayList(path));
return;
}
//单层递归逻辑
//不是0开始,而是1
for(int i = beginIndex;i<=n;i++){
path.add(i);
//递归
backingTracking(n,k,i+1);
//回溯
path.removeLast();
}
}
}剪枝优化
对上一道题做优化,并分析剪枝的套路都有哪些。

回溯算法做剪枝,就是在for循环这里做文章,减小范围
要选k个元素,已经选了path.size(),还需要选取k-path.size个元素
例子:要从5个元素里面找3个元素,右面边界最多到5-3+1=3,? a b c d e,也就是c的位置,因为从这之后,比如从d开始选,就小于3个了。这就是至多到n-(k-path.size())的原因
class Solution {
private List<Integer> path = new ArrayList<>();
private List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backingTracking(n,k,1);
return result;
}
void backingTracking(int n,int k,int beginIndex){
if(path.size()==k){
//收割结果
result.add(new ArrayList(path));
return;
}
//单层递归逻辑
//不是0开始,而是1
for(int i = beginIndex;i<=n-(k-path.size())+1;i++){
path.add(i);
//递归
backingTracking(n,k,i+1);
//回溯
path.removeLast();
}
}
}
文章来源:https://blog.csdn.net/weixin_65728526/article/details/135153496
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 多分支机构大型企业如何高效运维管理?向日葵x金地商置案例分享
- Delphi 支持的平台和操作系统 (XE4~D12)
- 贯穿设计模式-享元模式思考
- 【python】Python 3.11不支持Tix库
- 技术写作概述:内容分析、平台和转化追踪以及内容老化
- 导入和导出功能的简单实现
- 线性代数第三课+第四课
- Linux操作系统基础(二)系统的基础设置
- 我国“重要数据”方向要点、思考实践路径
- 写给后端的Docker初级入门教程:基础篇