42.接雨水

42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

思路：

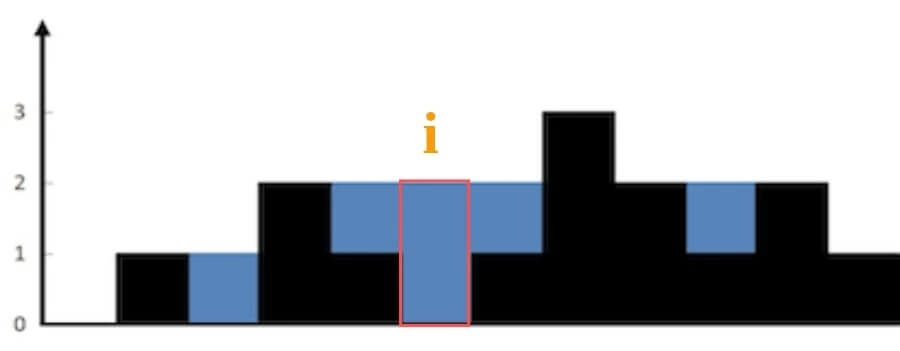
对于这种题，不要想整体，而应该去想局部，仅仅对于位置 i，能装下多少水呢，和左右两边最高高度相关。

如图：

能装 2 格水，因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。

为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 leftMax 和 rightMax；位置 i 最大的水柱高度就是 min(leftMax, rightMax)。

water[i] = min(
               # 左边最高的柱子
               max(height[0..i]),  
               # 右边最高的柱子
               max(height[i..end]) 
            ) - height[i]

本道题，可以看做每个位置能装多少水的相加和。

双指针同时开两个柱子接水。 对于每一个柱子接的水，那么它能接的水=min(左右两边最高柱子）-当前柱子高度，这个公式没有问题。同样的，两根柱子要一起求接水，同样要知道它们左右两边最大值的较小值。

问题就在这，假设两柱子分别为 i，j。那么就有 iLeftMax,iRightMax,jLeftMx,jRightMax 这个变量。由于 j>i ，故 jLeftMax>=iLeftMax，iRigthMax>=jRightMax.

那么，如果 iLeftMax>jRightMax，则必有 jLeftMax >= jRightMax，所有我们能接 j 点的水。

如果 jRightMax>iLeftMax，则必有 iRightMax >= iLeftMax，所以我们能接 i 点的水。

而上面我们实际上只用到了 iLeftMax，jRightMax 两个变量，故我们维护这两个即可。（题解都没说清楚，就说个 LeftMax，RightMax，谁知道为什么就可以这么做了。)

为什么上述中，由于 j>i ，故 jLeftMax>=iLeftMax，iRigthMax>=jRightMax 请教下如何得出这个结论？

jLeftMax >= iLeftMax 这个不是显然吗，j左边的元素包含了i左边的所有元素，如果非要证明一下的话， 那么， iLeftMax = Math.max( height[0], height[1] … height[i - 1], height[i] ) ①， jLeftMax = Math.max( height[0], height[1] … height[i - 1], height[i], height[i + 1] … height[j - 1], height[j] ) ②， 即 jLeftMax = Math.max( Math.max( height[0], height[1] … height[i - 1], height[i] ) , height[i + 1] … height[j - 1], height[j] ) ③， 将 ①式 代入 ③式 得： jLeftMax = Math.max( iLeftMax , height[i + 1] … height[j - 1], height[j] ) ④， 由反证法可知 若 jLeftMax < iLeftMax , 则 ④式 不成立， 故 jLeftMax >= iLeftMax， 同理可得：iRigthMax >= jRightMax。

//官方题解
public class Problem_0042_TrappingRainWater {
    public int trap(int[] height) {
        int ans = 0;
        int left = 0, right = height.length - 1;
        int leftMax = 0, rightMax = 0;
        while (left < right) {
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                left++;
            } else {
                ans += rightMax - height[right];
                --right;
            }
        }
        return ans;
    }
}