力扣：452. 用最少数量的箭引爆气球（贪心）

题目：

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。
示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。
示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:

• 在x = 2处发射箭，击破气球[1,2]和[2,3]。
• 在x = 4处射出箭，击破气球[3,4]和[4,5]。

提示:

1 <= points.length <= 105
points[i].length == 2
-231 <= xstart < xend <= 231 - 1

思路：

局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。 局部最优推出全局最优，所以是贪心思想。
为了让气球尽可能的重叠，需要对数组进行排序。

那么按照气球起始位置排序，还是按照气球终止位置排序呢？

其实都可以！只不过对应的遍历顺序不同，这里就按照气球的起始位置排序了。

既然按照起始位置排序，那么就从前向后遍历气球数组，靠左尽可能让气球重复。

从前向后遍历遇到重叠的气球了怎么办？

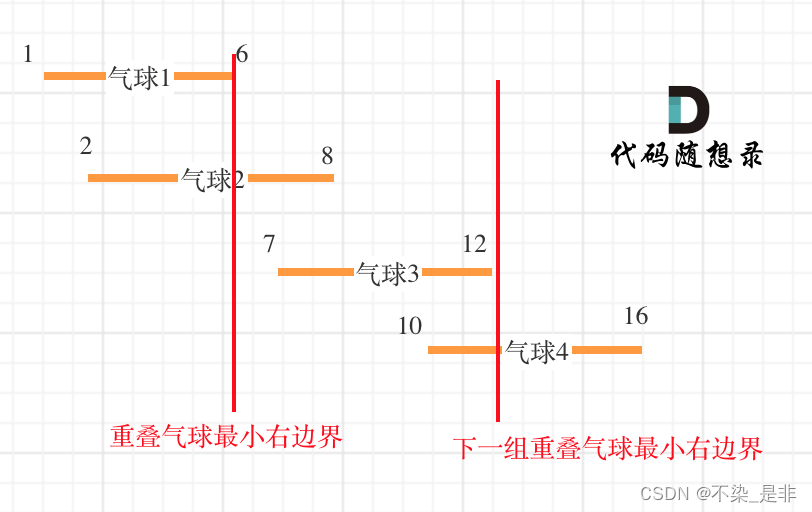
如果气球重叠了，重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭。

这么说可能不太好理解，下面结合具体代码给大家进行说明。

对于排好序的points（气球），从第二（i）个气球开始遍历，如果第i个气球的左边界大于第i-1个气球的右边界，则说明这两个气球不重叠，箭的数量+1
代码如下：

        for i in range(1, len(points)):
            # 如果当前区间起始点大于前一个区间的结束点，说明需要新增一支箭
            if points[i][0] > points[i - 1][1]:
                result += 1

这个很好理解，那么重叠了呢？重叠的情况就是第i个气球的左边界小于等于第i-1个气球的右边界，这是两个气球的重叠情况，那么第三个气球也重叠呢？

此时就需要对前两个气球的右边界进行重新定义（因为第i个气球始终是和第i-1个气球的右边界进行比较，所以需要重新定义右边界），那么如何定义呢？

如果重叠，则第i个气球的右边界等于第i个气球的右边界和第i-1个气球的右边界的最小值（因为排序是按照左边界进行排序的，所以右边界大小不能确定），只有这样才能判断第三个气球是否需要额外的箭。
代码如下：

            else:  # points[i][0] <= points[i - 1][1]:
                # 如果当前区间起始点小于前一个区间的结束点，更新当前区间的结束点为两个区间结束点的最小值
                points[i][1] = min(points[i][1], points[i - 1][1])

这里放一个代码随想录的图方便大家理解：

完整代码：

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        # 按照区间起始点对points进行排序
        points.sort(key = lambda x: x[0])
        result = 1
        for i in range(1, len(points)):
            # 如果当前区间起始点大于前一个区间的结束点，说明需要新增一支箭
            if points[i][0] > points[i - 1][1]:
                result += 1
            else:
                # 如果当前区间起始点小于前一个区间的结束点，更新当前区间的结束点为两个区间结束点的最小值
                points[i][1] = min(points[i][1], points[i - 1][1])
        return result