【拆盲盒02】算法题
题目 :
假设顺序表L中的元素按从小到大的次序排列,编写算法删除顺序表中“多余”的数据元素,即操作之后的顺序表中所有元素的值都不相同,要求时间尽可能的少;并对顺序表A(1,1,2,2,2,3,4,5,5,5,6,6,7,7,8,8,8,9)模拟执行本算法,并统计移动元素的次数。
我一开始看见这个题的时候,第一时间想到了"序列去重",然后自然而然想到了使用哈希表哈哈哈,然后这道题就被我搞复杂了,我的复杂思路如下,不建议采用我这种方式解题哦~
要在Java中去除顺序表中的重复元素而不改变元素的原始顺序,可以结合使用哈希表(或HashSet)和ArrayList。HashSet用于追踪已经出现过的元素,而ArrayList用于存储去除重复后的元素。这个方法保持了元素的原始顺序并且去除了重复项。
同时,这个方法的时间复杂度是O(n),其中n是输入数组的长度,因为每个元素只被遍历一次。由于HashSet的添加和查找操作通常是O(1)的,因此这种方法是高效的。
以下就是一个Java代码实现上述的逻辑 :
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class RemoveDuplicates {
public static void main(String[] args) {
// 示例数组
int[] nums = {1,2,2,2,2,3,4,5,5,5,6,6,7,7,8,8,8,9};
// 调用函数去除重复元素
List<Integer> result = removeDuplicates(nums);
// 打印结果
for (int num : result) {
System.out.print(num + " ");
}
}
public static List<Integer> removeDuplicates(int[] nums) {
Set<Integer> seen = new HashSet<>();
List<Integer> result = new ArrayList<>();
for (int num : nums) {
if (!seen.contains(num)) {
seen.add(num);
result.add(num);
}
}
return result;
}
}
要实现移动元素计数的功能,我们可以引入一个计数器变量来跟踪添加到result数组中的每个元素。每当我们向result中添加一个元素时,就增加这个计数器的值。
-
问: 为什么移动元素的次数就是最后元素的个数 ?
- 答 : 移动元素的次数与最终元素的个数相同的原因在于你的算法实际上是在创建一个新的列表(result),并将原列表(arrayList)中未重复的元素“移动”到这个新列表中。在这个过程中,每当你遇到一个尚未存在于HashSet中的元素,你就将它添加到result中。这个添加操作可以被视作是一次“移动”。
- 这里的“移动”是一个比喻。在实际编程中,你并没有从原列表中删除元素再添加到新列表中,而是在新列表中创建了一个元素的副本。但从逻辑上讲,你可以将这个过程视为“移动”一个元素,因为每个元素最终都从原始位置(在arrayList中)“移动”到了新位置(在result中)。
- 因此,每添加一个新元素到result中,实际上就是完成了一次“移动”,而最终result中元素的总数即为移动元素的次数。这也是为什么移动元素的次数等于最终元素的个数。
?
如下 : 修正后的代码(加上了计数器)
public static void removeDuplicates(ArrayList<Integer> arrayList){
HashSet<Integer> key = new HashSet<>();
ArrayList<Integer> result = new ArrayList<>();
int moveCount = 0;
for (int num : arrayList) {
if (!key.contains(num)) {
key.add(num);
result.add(num);
moveCount++; // 增加移动次数
}
}
System.out.println("移动元素的次数: " + moveCount);
for (int num : result) {
System.out.print(num + " ");
}
}
最后我就去搜罗搜罗,发现了非常非常巧妙的方法,没有使用额外的空间,仅仅在原数组上面进行操作就完成了对序列去重的操作,而且还没有改变序列中各个元素的顺序,Java代码如下,光看下面的这几行代码,感觉不是非常直观,所以我还是用图把这个逻辑实现出来,这样理解起来也会更加的容易~
先来对这个代码进行一个逻辑上的解释,我们要知道,这个方法只能用在特定的场景,也就是只能拿来解特定的题目,这里的数组A必须是已经有序的才可以使用.
- 循环遍历: 使用一个循环来遍历数组 A 的每个元素。
- 去重判断: 通过判断 A[i] != A[i - 1]来识别是否有重复的元素。这意味着,这个方法假设数组 A 已经是排序过的。如果数组 A 未排序,这个判断将不准确。
- 元素复制: 如果发现一个不重复的元素(或者是数组的第一个元素),它会被复制到数组的 t索引位置。
- 返回值: 返回 t,即不重复元素的数量。
图示

一步一步拆解的示意图
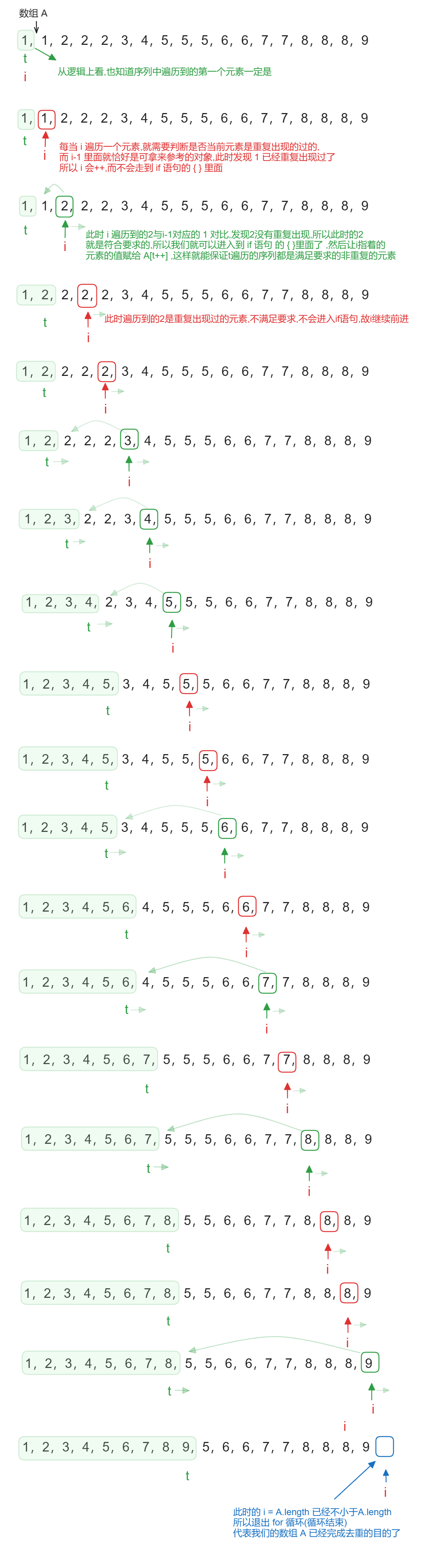
Java代码
public int distinct(int[] A) {
int t = 0;
for (int i = 0; i < A.length; i++) {
if (i == 0 || A[i] != A[i - 1]) A[t++] = A[i];
}
return t;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2024 前端高频面试题之 Vue 篇
- VUE3好看的我的家乡网站模板源码
- 网络安全(黑客)—自学
- 蓝桥杯备赛 | 洛谷做题打卡day2
- 如何使用 Python 解决网络抓取中的 reCAPTCHA 问题
- JavaScript中的函数对象和命名函数表达式(NFE)
- C#,入门教程(66)——枚举Enum的高等用法
- 【实时绘画】comfyUI 实时绘画工作流 - 本地
- VS Code 配置 Vue3 模板 详细步骤
- android 分享文件