数据结构之＜堆＞的介绍

1.简介

---

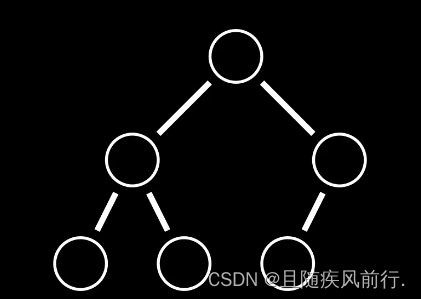
堆是一种特殊的数据结构，通常用于实现优先队列。堆是一个可以被看作近似完全二叉树的结构，并且具有一些特殊的性质，根据这些性质，堆被分为最大堆（或者大根堆，大顶堆）和最小堆两种。

2.基本性质

---

1. 完全二叉树结构：堆必须是一棵完全二叉树，即除了最底层，其他层都是满的，而且最底层的节点都尽量靠左排列，最后一行元素之间不可以有间隔。
2. 堆序性质： 堆分为最大堆和最小堆两种。在最大堆中，任意节点的值都大于或等于其子节点的值；在最小堆中，任意节点的值都小于或等于其子节点的值。

3.节点下标间的规律

---

因为堆是一棵完全二叉树若父节点的下标为i，则左子节点下标为2i+1,右子节点下标为2i+2,这个规律会在算法排序中经常使用。

4.堆的基本操作

---

上滤（Percolate Up）

上滤是指在堆中插入新元素后，通过一系列的比较和交换操作将该元素上移到合适的位置，以保持堆的堆序性。通常用于最小堆和最大堆中。

步骤：

1. 将新元素插入到堆的末尾（底部）。
2. 比较该元素与其父节点的值。
3. 如果该元素的值比父节点的值更小（对于最小堆）或更大（对于最大堆），则交换它们。
4. 重复步骤2和步骤3，直到满足堆的性质为止。

下滤（Percolate Down）

下滤是指在删除堆顶元素后，通过一系列的比较和交换操作将堆的最后一个元素（通常是堆底元素）移到堆顶，并将其下移到合适的位置，以保持堆的堆序性。

步骤：

1. 将堆的最后一个元素（通常是堆底元素）移到堆顶。
2. 比较该元素与其子节点中较小（对于最小堆）或较大（对于最大堆）的一个。
3. 如果该元素的值比子节点的值更小（对于最小堆）或更大（对于最大堆），则交换它们。
4. 重复步骤2和步骤3，直到满足堆的性质为止。

应用场景：

• 上滤： 通常在插入新元素时使用，确保新元素的插入不破坏堆的性质。
• 下滤： 通常在删除堆顶元素后使用，以恢复堆的性质。

3.堆化（Heapify）

堆化（Heapify）是指将一个无序的序列转换成一个堆，可以是最小堆或最大堆。堆化过程可以分为两种：自底向上堆化（Bottom-Up Heapify）和自顶向下堆化（Top-Down Heapify）。

自底向上堆化（Bottom-Up Heapify）：

自底向上堆化是从序列的最后一个非叶子节点开始，逐步向前处理每个节点，使得以该节点为根的子树成为一个堆。该方法保证了子树堆化后，整个序列也是一个堆。

步骤：

1. 从序列的最后一个非叶子节点开始（通常是 n/2-1，其中 n 是序列的长度）。

2. 对每个非叶子节点，与其子节点比较，如果不满足堆的性质，则进行交换。

3. 重复上述步骤，直到处理完整个序列。

自顶向下堆化（Top-Down Heapify）：

自顶向下堆化是从序列的第一个元素开始，逐步向后处理每个节点，使得以该节点为根的子树成为一个堆。该方法保证了每个节点都满足堆的性质。

步骤：

1. 从序列的第一个元素开始。

2. 对每个节点，与其子节点比较，如果不满足堆的性质，则进行交换。

3. 重复上述步骤，直到处理完整个序列。

应用场景：

• 建堆： 堆化是建立堆的关键步骤，可以在 O(n) 的时间复杂度内将一个无序序列转化为堆。
• 堆排序： 在堆排序算法中，首先对待排序序列进行堆化，然后反复取出堆顶元素，直到堆为空，实现排序。
• 优先队列： 堆被广泛应用于实现优先队列，堆化操作确保队列中优先级最高的元素位于队首。