二叉树的层序遍历经典问题（算法村第六关白银挑战）

发布时间：2024年01月05日

基本的层序遍历与变换

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

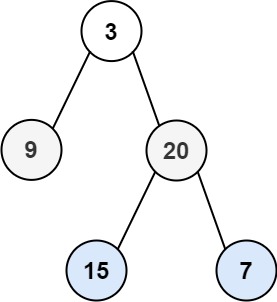
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

解

public static List<List<Integer>> levelOrder(TreeNode root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<List<Integer>>();

    ArrayList<List<Integer>> ans = new ArrayList<>();

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
       //获取当前层的结点个数
       int size = queue.size();
            
       //该层结点的值
       ArrayList<Integer> list = new ArrayList<>();

        //遍历当前层
        for (int i = 0; i< size; i++)
        {
            TreeNode t = queue.remove();
            list.add(t.val);

            if (t.left != null)
                queue.offer(t.left);
            if (t.right != null)
                queue.offer(t.right);
        }

        //将这一层结点的值加入答案
        ans.add(list);
    }

    return ans;
}

自底而上的层序遍历

107. 二叉树的层序遍历 II - 力扣（LeetCode）

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

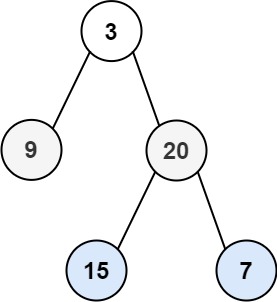
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

解

在遍历完一层节点之后，将存储该层节点值的列表 list 添加到结果列表 ans 的头部即可。

为了时间复杂度，ans 使用链式结构的结构。在 ans 头部添加一层节点值的列表 list 的时间复杂度是 O(1)

public List<List<Integer>> levelOrderBottom(TreeNode root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<List<Integer>>();

    ArrayList<List<Integer>> ans = new ArrayList<>();

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //该层结点的值
        ArrayList<Integer> list = new ArrayList<>();

        //遍历当前层
        for (int i = 0; i< size; i++)
        {
            TreeNode t = queue.remove();
            list.add(t.val);

            if (t.left != null)
                queue.offer(t.left);
            if (t.right != null)
                queue.offer(t.right);
        }

        //将这一层结点的值插入答案的头部
        ans.add(0,list);
    }

    return ans;
}

锯齿形层序遍历

103. 二叉树的锯齿形层序遍历 - 力扣（LeetCode）

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

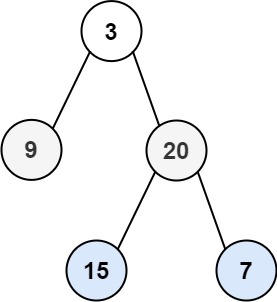
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

用双端队列维护当前层节点的存储

双端队列可以队头或队尾插入元素。

层序遍历顺序不变，但对当前层节点的存储，我们维护一个变量 isOrderLeft ，记录结点存储是从左至右还是从右至左

若从左至右，则采用头插法。该层第一个元素在此层遍历结束后，会出现在list的末端
若从右至左，则采用尾插法。该层第一个元素在此层遍历结束后，会出现在list的首端

最后需要注意的是，往 ans 添加 list 时，需要转换一下 list 的类型

public List<List<Integer>> zigzagLevelOrder(TreeNode root)
    {
        //特判，否则queue.offer(root)会抛出NullPointerException
        if (root == null)
            return new ArrayList<List<Integer>>();

        ArrayList<List<Integer>> ans = new ArrayList<>();

        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);

        boolean isOrderLeft = true;

        while (!queue.isEmpty())
        {
            //获取当前层的结点个数
            int size = queue.size();

            //该层结点的值。用一个双端队列存储
            ArrayDeque<Integer> deque = new ArrayDeque<>();

            //遍历当前层
            for (int i = 0; i< size; i++)
            {
                TreeNode t = queue.remove();

                if (isOrderLeft)
                    deque.offerLast(t.val);
                else
                    deque.offerFirst(t.val);

                if (t.left != null)
                    queue.offer(t.left);
                if (t.right != null)
                    queue.offer(t.right);
            }

            //这一层结点的值经过转换后加入答案
            ans.add(new LinkedList<>(deque));

            isOrderLeft = !isOrderLeft; //交替进行
        }

        return ans;
    }

N叉树的层序遍历

429. N 叉树的层序遍历 - 力扣（LeetCode）

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

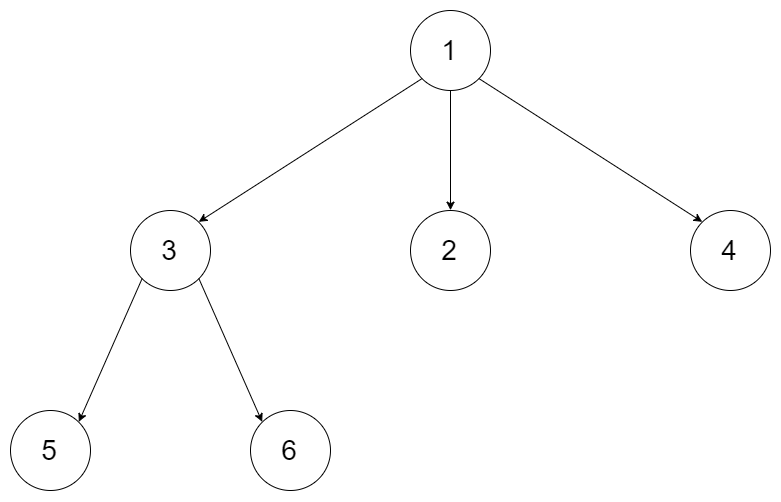
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

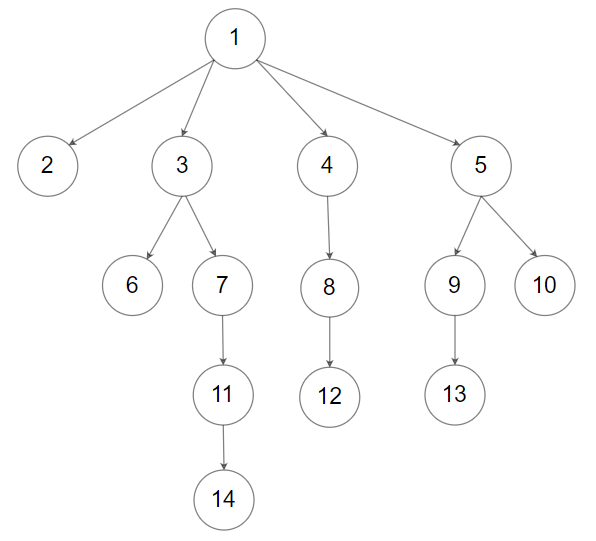
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

结点类型

public class Node
{
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
}

解

public List<List<Integer>> levelOrder(Node root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<List<Integer>>();

    ArrayList<List<Integer>> ans = new ArrayList<>();

    ArrayDeque<Node> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //该层结点的值
        ArrayList<Integer> list = new ArrayList<>();

        //遍历当前层
        for (int i = 0; i< size; i++)
        {
            Node t = queue.remove();
            list.add(t.val);

            //将当前结点的所有孩子加入队列
            for (Node child : t.children)
            {
                queue.offer(child);
            }
        }

        //将这一层结点的值加入答案
        ans.add(list);
    }

    return ans;
}

处理每层元素

在每个树行中找最大值

515. 在每个树行中找最大值 - 力扣（LeetCode）

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

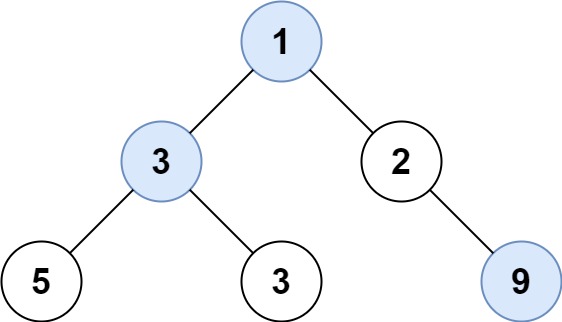
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

维护每层的最大值即可

public List<Integer> largestValues(TreeNode root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<>();

    //存储每层结点的最大值
    ArrayList<Integer> list = new ArrayList<>();

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //当前层结点的最大值
        int maxOfLevel = Integer.MIN_VALUE;

        //遍历当前层
        for (int i = 0; i< size; i++)
        {
            TreeNode t = queue.remove();

            maxOfLevel = Math.max(maxOfLevel, t.val);

            if (t.left != null)
                queue.offer(t.left);
            if (t.right != null)
                queue.offer(t.right);
        }

        list.add(maxOfLevel);
    }

    return list;
}

二叉树的层平均值

637. 二叉树的层平均值 - 力扣（LeetCode）

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

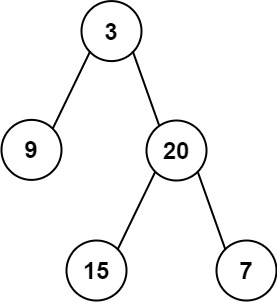
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

解

public List<Double> averageOfLevels(TreeNode root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<>();

    //存储每层结点的最大值
    ArrayList<Double> list = new ArrayList<>();

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //当前层结点值的和
        double sum = 0;

        //遍历当前层
        for (int i = 0; i< size; i++)
        {
            TreeNode t = queue.remove();

            sum += t.val;

            if (t.left != null)
                queue.offer(t.left);
            if (t.right != null)
                queue.offer(t.right);
        }
		
        //计算平均值并添加到列表
        list.add(sum / size);
    }

    return list;
}

二叉树的右视图

199. 二叉树的右视图 - 力扣（LeetCode）

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

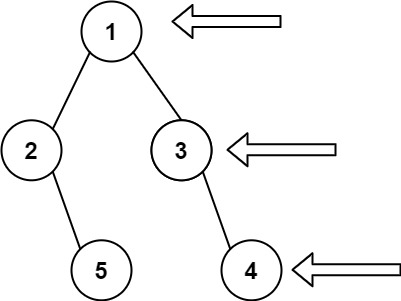
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

解

层序遍历，记录每层最后一个元素即可

public List<Integer> rightSideView(TreeNode root)
{
    //特判，否则queue.offer(root)会抛出NullPointerException
    if (root == null)
        return new ArrayList<>();

    //存储每层的最后一个结点
    ArrayList<Integer> list = new ArrayList<>();

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //遍历当前层
        for (int i = 0; i < size; i++)
        {
            TreeNode t = queue.remove();

            //记录当前层最后一个元素
            if (i == size - 1)
                list.add(t.val);

            if (t.left != null)
                queue.offer(t.left);
            if (t.right != null)
                queue.offer(t.right);
        }
    }

    return list;
}

最底层最左边的结点

513. 找树左下角的值 - 力扣（LeetCode）

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

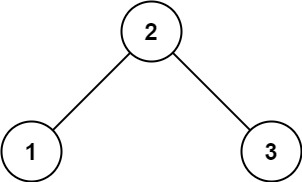
输入: root = [2,1,3]
输出: 1

示例 2:

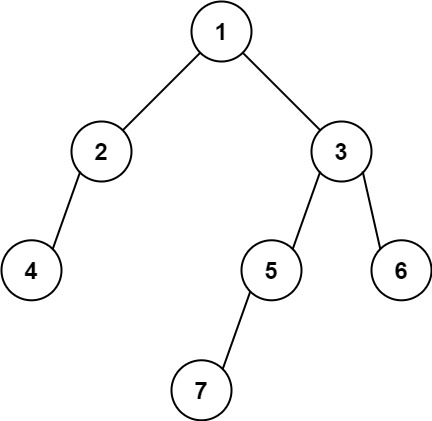
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

从右往左层序遍历

从右向左层次遍历，最后一个访问的节点必然是最底层最左侧叶子节点。只需调整一下左右孩子加入队列的次序即可

public int findBottomLeftValue(TreeNode root)
{
    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);

    TreeNode t = null;

    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //遍历当前层
        for (int i = 0; i < size; i++)
        {
            t = queue.remove();

            //右孩子先于左孩子放入队列
            if (t.right != null)
                queue.offer(t.right);
            if (t.left != null)
                queue.offer(t.left);
        }
    }

    return t.val;   //返回最底层最右边的结点的值
}

左叶子之和

404. 左叶子之和 - 力扣（LeetCode）

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

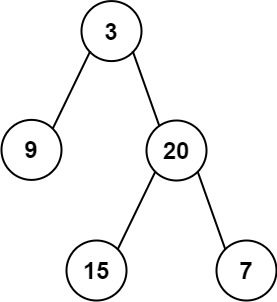
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

提示:

节点数在 [1, 1000] 范围内

广度优先遍历

在BFS的过程中添加一个判断是否为左叶子结点的条件语句即可

public int sumOfLeftLeaves(TreeNode root)
{
    int answer = 0;

    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);


    while (!queue.isEmpty())
    {
        //获取当前层的结点个数
        int size = queue.size();

        //遍历当前层
        for (int i = 0; i < size; i++)
        {
            TreeNode t = queue.remove();

            if (t.left != null)
            {
                //如果t的左孩子是叶子结点
                if(t.left.left == null && t.left.right == null)
                    answer += t.left.val;
                else
                    queue.offer(t.left);
            }
            if (t.right != null)
                queue.offer(t.right);

        }
    }

    return answer;
}

文章来源:https://blog.csdn.net/cjj2543107638/article/details/135411173
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！