C++ STL -＞priority_queue(优先级队列)

优先级队列：
priority_queue文档

1. 优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。

2. 此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元 素)

3. 优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特 定的成员函数来访问其元素。元素从特定容器的“尾部”弹出，其称为优先队列的顶部。

4. 底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。容器应该可以通过随机访问迭 代器访问，并支持以下操作：

   • empty()：检测容器是否为空
   • size()：返回容器中有效元素个数
   • front()：返回容器中第一个元素的引用
   • push_back()：在容器尾部插入元素
   • pop_back()：删除容器尾部元素

5. 标准容器类vector和deque满足这些需求。默认情况下，如果没有为特定的priority_queue类实例化指 定容器类，则使用vector。

6. 需要支持随机访问迭代器，以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数 make_heap、push_heap和pop_heap来自动完成此操作。

priority_queue的使用

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成 堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。

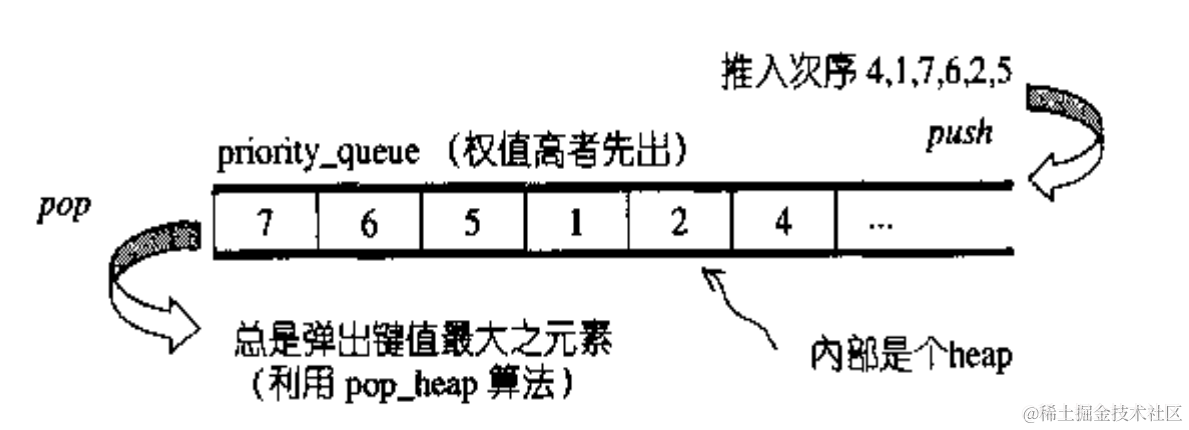
默认情况下priority_queue是大堆

int main()
{
    vector<int> v{3,1,56,7,9,5,2,58,79,};
    priority_queue<int> mypq;
    //将vector中的数据依次入队列
    for (auto& e : v)
    {
        mypq.push(e);
    }
    //mypq中的数据已经是有序的了
    while (!mypq.empty()) 
    {
        cout << mypq.top() << ' ';
        mypq.pop();
    }
    return 0;
}

运行结果：

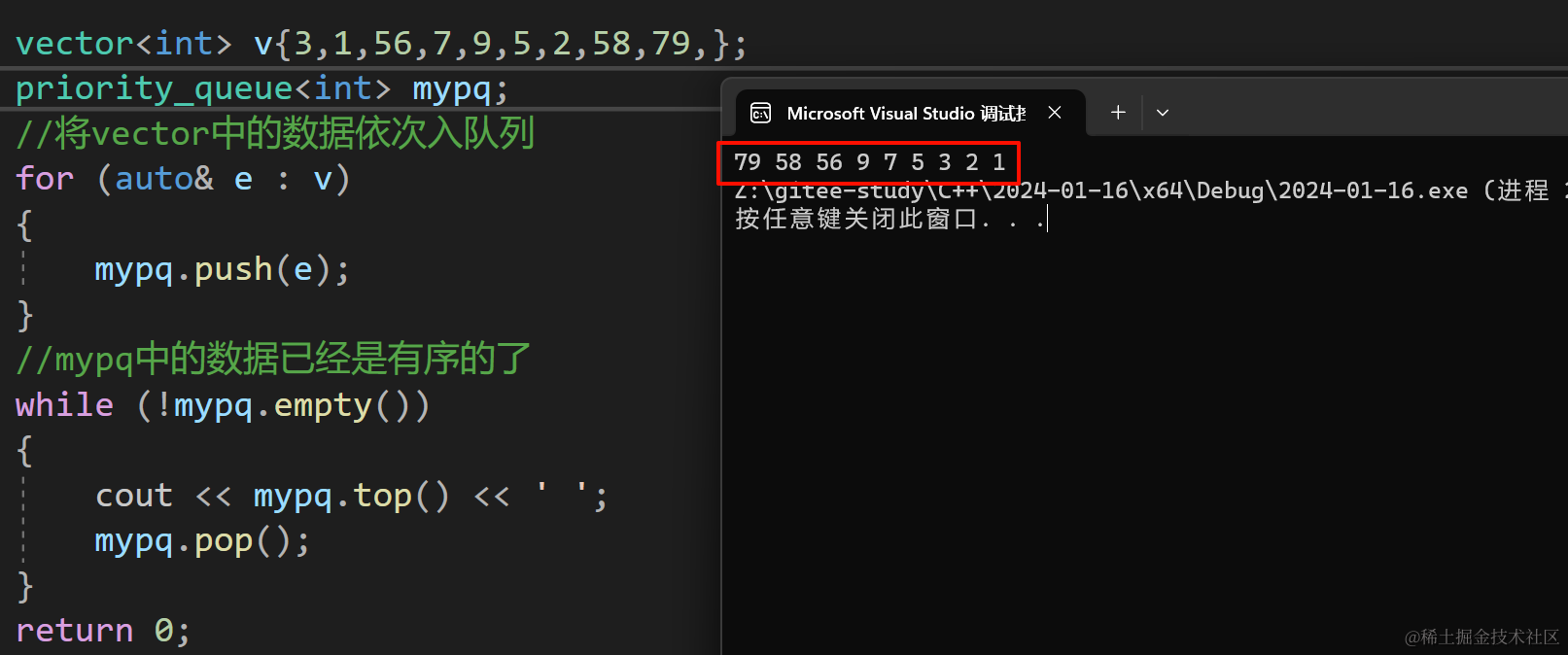
priority_queue建小堆

默认情况下priority_queue是大堆，如果需要小堆，就需要用到仿函数

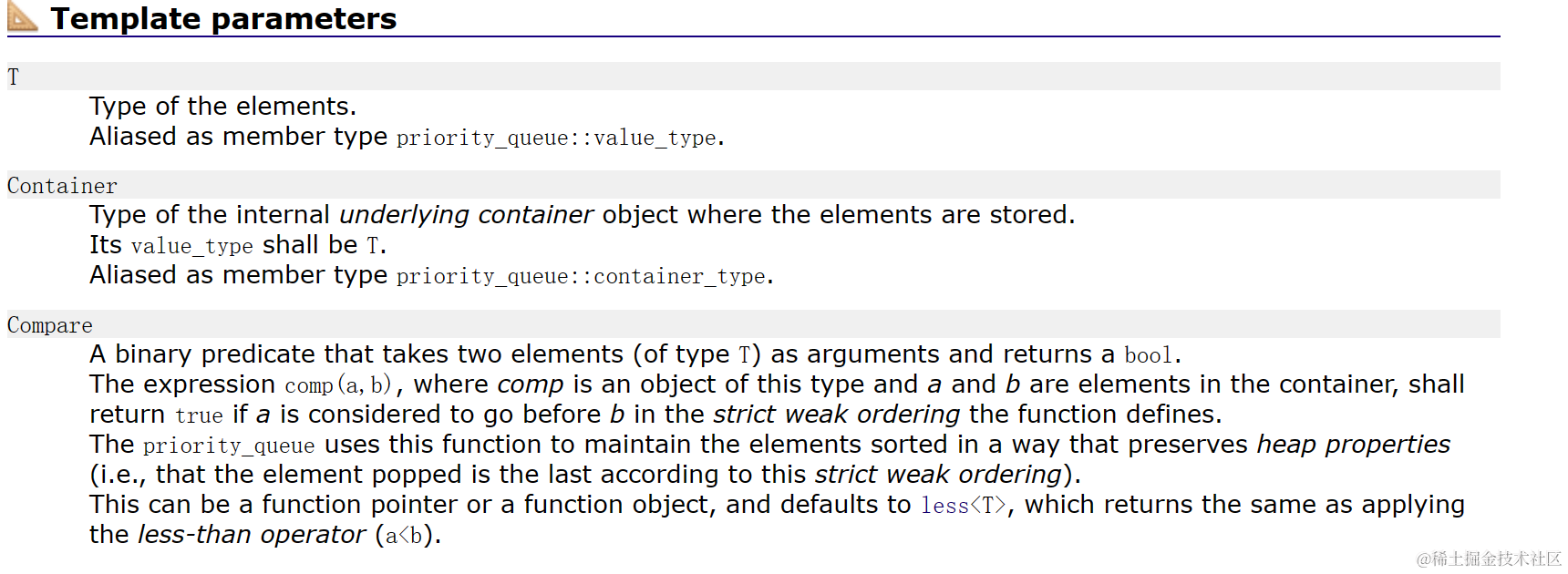
priority_queue类原型

template <class T, class Container = vector<T>,
          class Compare = less<typename Container::value_type> > class priority_queue;

• 第一个模板参数是数据类型(int,double、char等)
• 第二个参数是底层容器，默认是vector，也可以是list等
• 第三个参数就是仿函数 默认缺省值是less(大堆)，小堆的仿函数是greator

int main()
{

    vector<int> v{ 3,1,56,7,9,5,2,58,79, };
    //建小堆，第二个模板参数也必须要传，因为c++语法规定，半缺省参数必须从右向左依次给 不能间隔着给
    priority_queue<int,vector<int>,greater<int>> mypq;
    //将vector中的数据依次入队列
    for (auto& e : v)
    {
        mypq.push(e);
    }
    //mypq中的数据已经是有序的了
    while (!mypq.empty())
    {
        cout << mypq.top() << ' ';
        mypq.pop();
    }
    return 0;
}

运行结果：

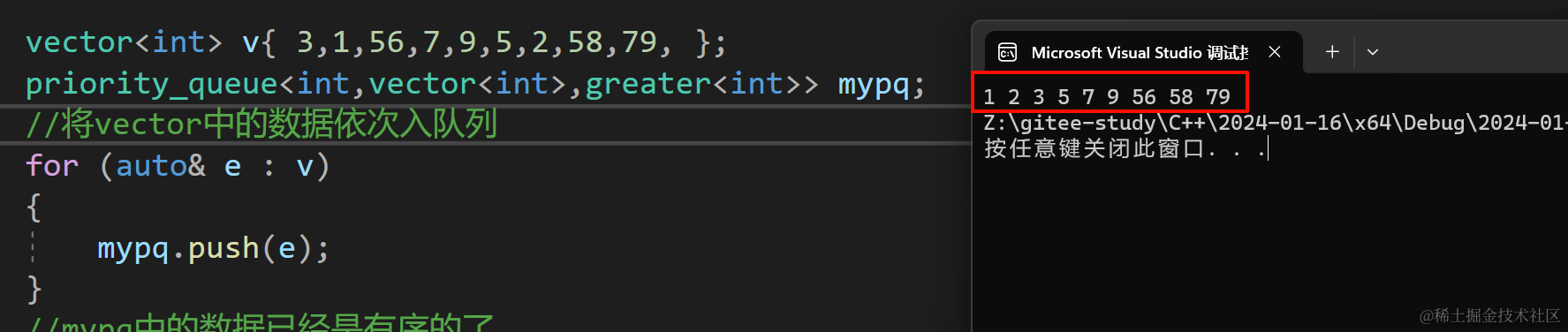
注意： 如果priority_queue中放的是自定义类型，那么自定义类要重载> 或者 < 操作符
比如 一个日期类

class Date
{
public:
	Date(int year = 1, int month  = 1, int day =  1)
		:_year(year)
		,_month(month)
		,_day(day)
	{}
	bool operator>(const Date& d)const
	{
		return (_year > d._year) ||
			   (_year == d._year && _month > d._month) ||
			   (_year == d._year && _month == d._month && _day > d._day);
	}
	bool operator<(const Date& d)const
	{
		return (_year < d._year) ||
			(_year == d._year && _month < d._month) ||
			(_year == d._year && _month == d._month && _day < d._day);
	}
	//  << 操作符是双操作数，成员函数有个默认的this指针，写为成员函数操作数就有三个了，所以要写在类外面
	//  <<操作符需要访问类的私有成员，声明为Date类的朋友就可以访问了
	//  << 返回ostream&是因为支持连续访问
	friend ostream& operator<<(ostream& _cout, const Date& d);
private:
	int _year;
	int _month;
	int _day;
};
ostream& operator<<(ostream& _cout, const Date& d)
{
	_cout << d._year << "-" << d._month << "-" << d._day;
	return _cout;
}
int main()
{
	//priority_queue存放自定义类型，自定义类型需要重载 < 或者 >运算符

	priority_queue<Date> datepq;
	datepq.push(Date(2023, 01, 26));
	datepq.push(Date(2024, 02, 26));
	datepq.push(Date(2023, 01, 21));
	datepq.push(Date(2021, 01, 26));
	while (!datepq.empty()) 
	{
		//自定义类型需要重载<<运算符
		cout << datepq.top() << endl;
		datepq.pop();
	}
  return 0;
}

力扣上的一道oj题，使用priority_queue来解决
题目链接：215. 数组中的第K个最大元素 - 力扣（LeetCode）

题目很简单就是返回数组中第k大的元素。
思路：将数组中的数据push到优先级队列中，然后pop ，k-1次即可

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        
        priority_queue<int> srotpq;
        for(auto &e : nums)
        {
            srotpq.push(e);
        }
        for(int i =0 ; i < k-1 ; ++i)
        {
            srotpq.pop();
        }
        return srotpq.top();
    }
};

这样解是没问题的，但是面试要是这样直接用STL库的话，容易回去等通知。因为面试主要考察的是用堆解决这个问题，而不是直接使用STL容器。下面就模拟实现一下STL中优先级队列建堆的过程。

priority_queue模拟实现

priority_queue类定义

namespace ding
{
   //第一个模板参数数元素类型，第二个数底层容器，第三个是仿函数，主要用来判断建大堆还是建小堆
   template <class T ,class Container = vector<T>,class Compare = less<T>>
   class priority_queue
   {
   public:
           bool empty();//判空
           size_t size();//队列中元素个数
           T top();//取队头元素
           void push(const T& val);//入队列
           void pop();//出队列
   private:
   Container _con;//底层容器 默认是vector
   }; 
}

empty

判断容器适配器是否为空，直接判断底层容器是否为空即可

bool empty() const
{
    return _con.empty();
}

size

返回适配器元素个数，直接返回底层容器元素个数即可

size_t size() const
{
    return _con.size();
}

top

返回队头元素，直接返回底层容器的第一个元素即可

T top() const
{
    return _con.front();
}

push

入队列，入完队列要经过堆排序算法确定元素的最终位置

比如 队列中已有元素【9，7，6，4】

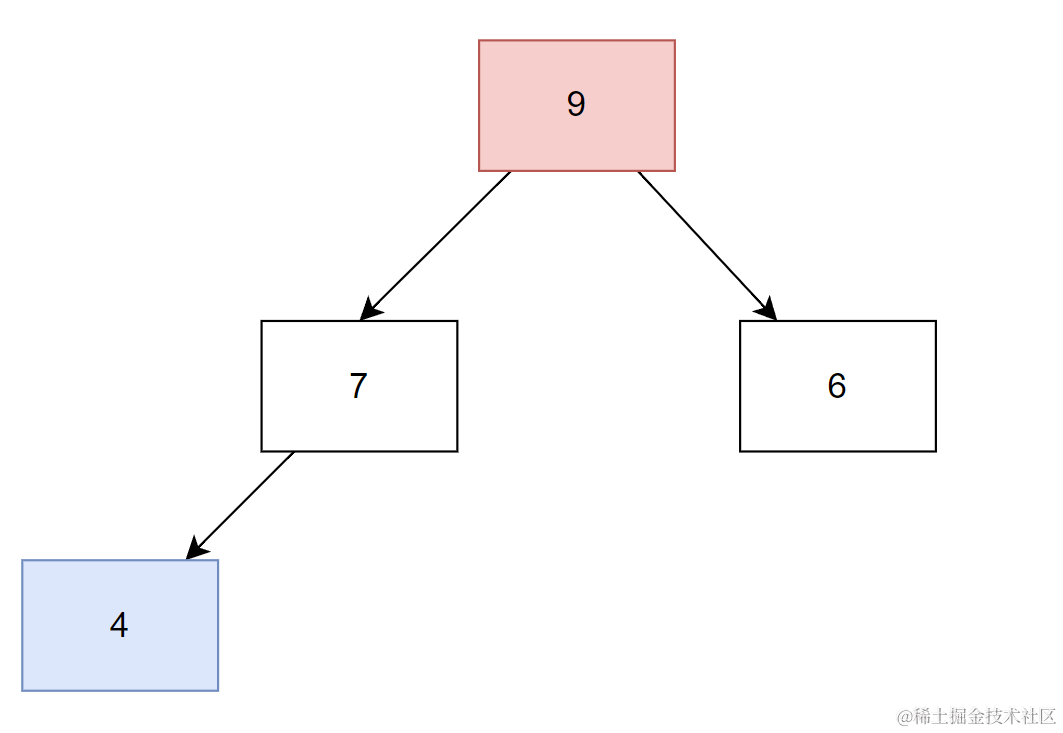
push 13 之后

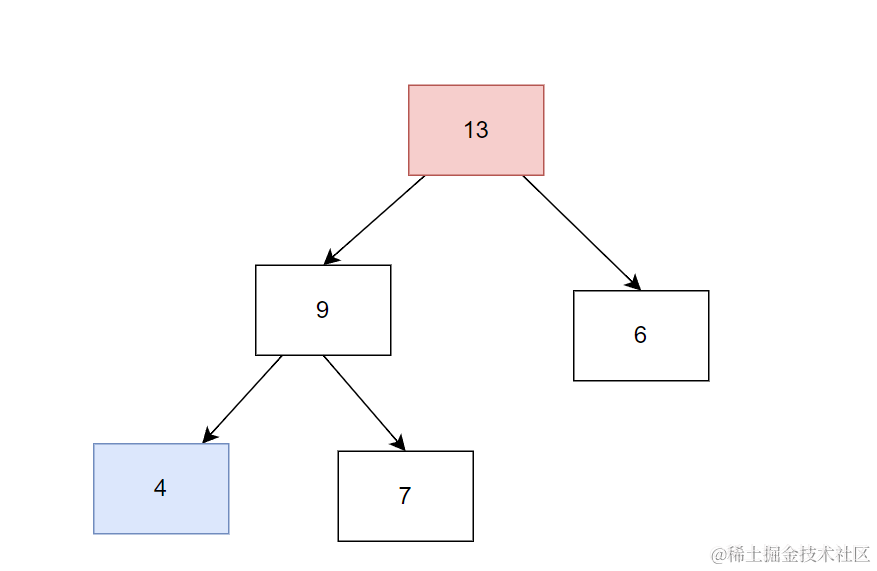
再继续push 8

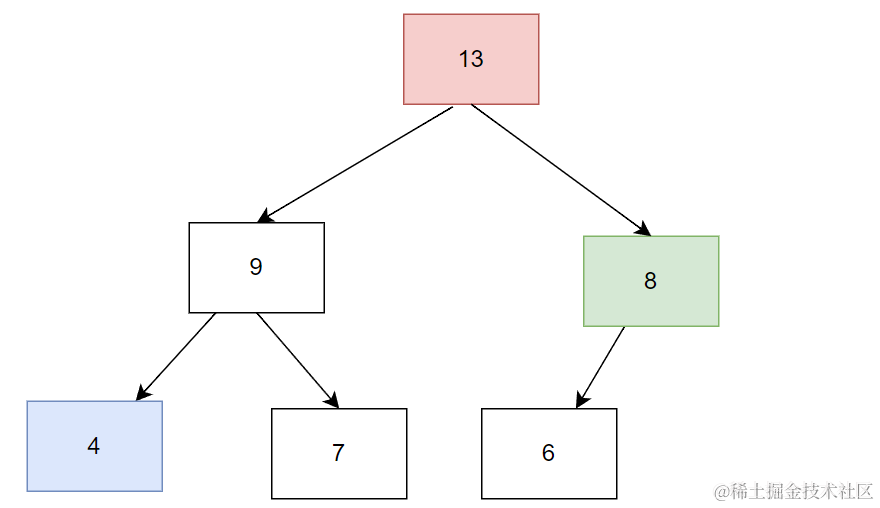
void adjust_up(int child)
{
    int parent = (child - 1) / 2; //找父结点
    while (child > 0) 
    {
        if (_con[child] > _con[parent])
        {
            swap(_con[child], _com[parent]);
            child = parent;
            parent = (child - 1) / 2;
        }
        else
        {
            break;
        }
    }
}
void push(const T& val)
{
    _con.push_back(val);//入队列
    adjust_up(_con.size()-1);//向上调整建堆
}

如果向上调整算法这样写，建小堆只能改代码。 解决这个问题，这里就用到了第三个模板参数 仿函数

仿函数

• 仿函数就是一个类中重载()运算符即可。
• 这样对象的调用方式就和函数的调用方式一样 一个是类名+(),一个是函数名+()。
• 这也是叫仿函数的原因。

//大堆传less
template<class	T>
struct less
{
    //lhs左操作数  rhs右操作数
    bool operator()(const T& lhs, const T& rhs)
    {
        return lhs < rhs;
    }
};

//小堆传greater
template<class	T>
struct greater
{
    //lhs左操作数  rhs右操作数
    bool operator()(const T& lhs, const T& rhs)
    {
        return lhs > rhs;
    }
};

使用仿函数和模板参数后的建堆算法如下

void adjust_up(int child)
{
    Compare _cmp;//仿函数对象(可以写为类的成员变量)
    int parent = (child - 1) / 2;
    while (child > 0)
    {
        if(_cmp(_con[parent],_con[child]))//仿函数对象调用()运算符进行比较
        {
            swap(_con[parent], _con[child]);
            child = parent;
            parent = (child - 1) / 2;
        }
        else
        {
            break;
        }
    }
}

pop

• 为了使出完队列内的数据仍然是堆的结构，需要在出队列之前先交换一下第一个和最后一个元素，再尾删最后一个。
• 如果直接头删第一个结点的话，堆的结构就被破坏了
• 删完之后，从根节点再进行一次调整的算法让队列中的数据仍然保持堆的结构。
  以大堆位列
  比如已有数据为：

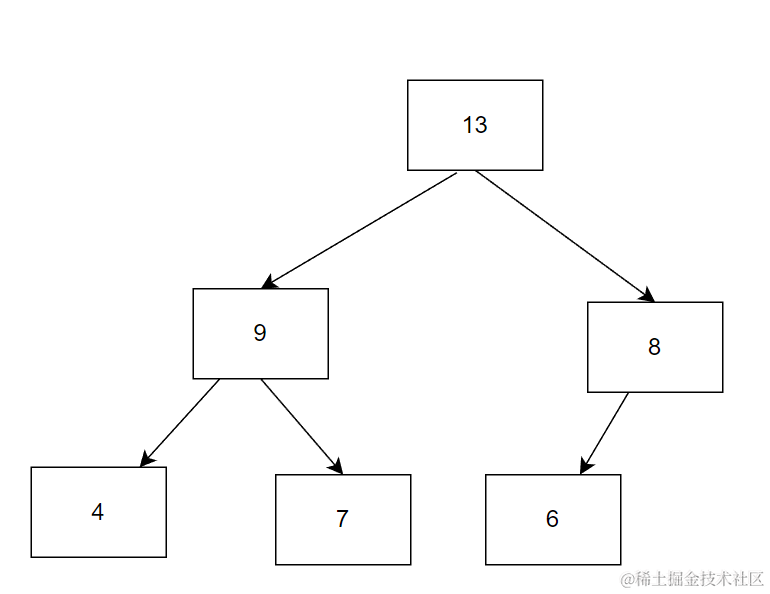
pop之前先交换

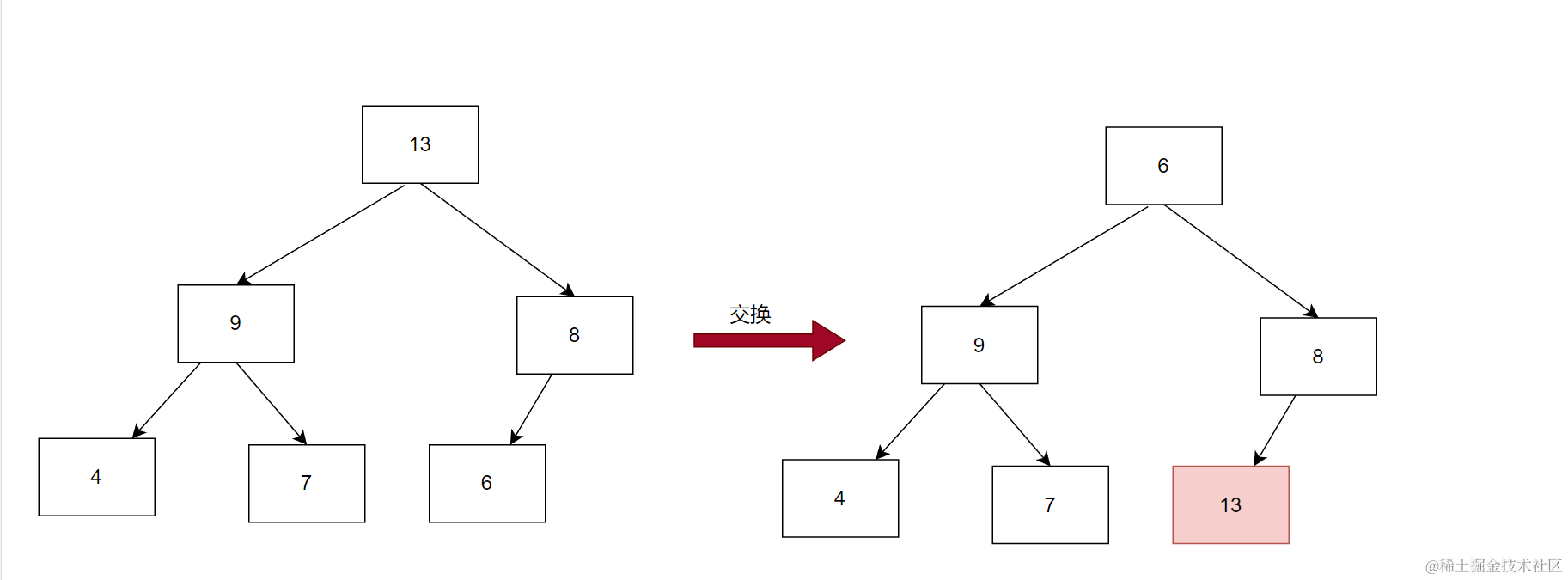
再尾删最后一个变为

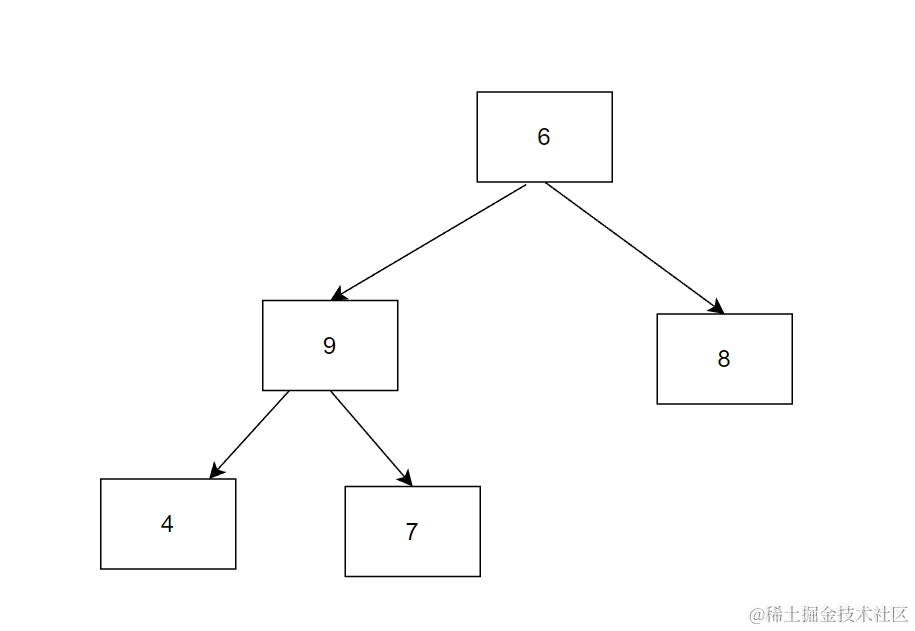
这样不是堆的结构，从根节点向下调整使成为堆

向下调整 让左后孩子大的那一个和根节点进行交换 变为

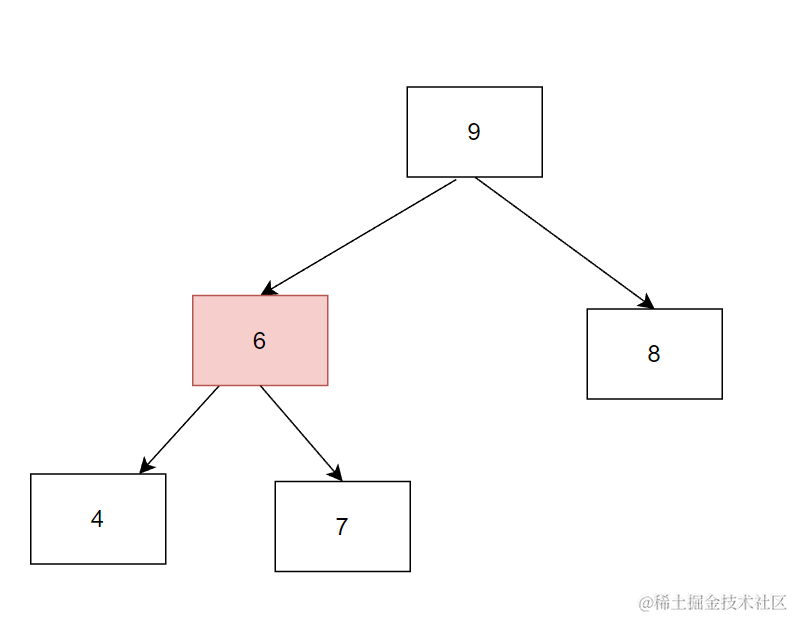
还不是堆的结构 继续向下调整

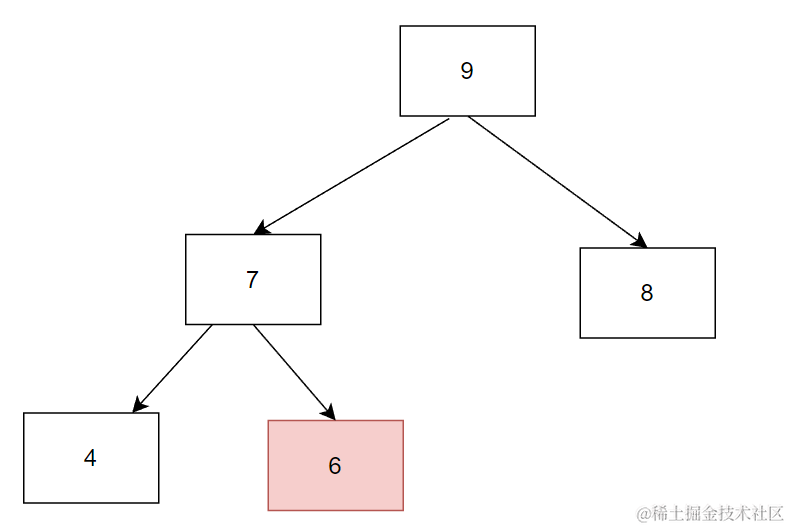
这样就是堆的结构了

void adjust_down(size_t parent) 
{
    size_t child = parent * 2 + 1;
    while (child < size())
    {
        Compare _com;//实例化一个对象，让对象去调用()重载
        if (child + 1  < size() && _com(_con[child],_con[child+1]))
        {
            ++child;
        }
        
        if (_com(_con[parent] , _con[child])) 
        {
            swap(_con[parent], _con[child]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}
// pop最大的 使剩下的元素继续保持堆得性质
void pop() 
{
    //交换第一个和最后一个
    std::swap(_con[0],_con[size()-1]);
    _con.pop_back();
    //向下调整建堆（从根结点向下调整）
    adjust_down(0);

}

参考源码

• gitee STL优先级队列模拟实现