RL的体悟以及简单的算法介绍
本文将围绕着本人在接触rl后的各种问题，简单解答，顺便介绍各种算法。主要是给自己用做笔记，所以写得比较乱。
0、 可以参考的资料
openai的教程 这个讲得很棒，最好可以按照顺序读一遍
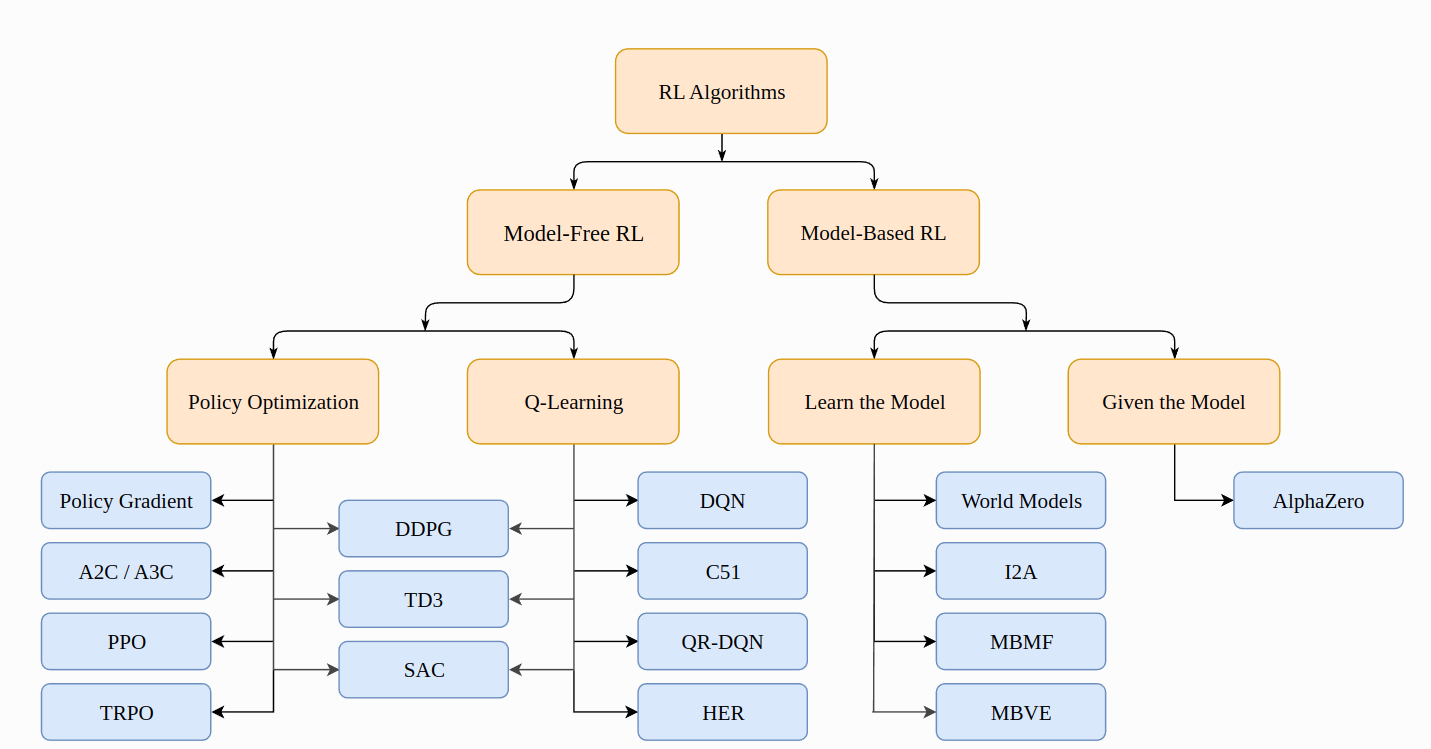
1、off policy / on policy?
off policy ：采样策略和目标策略不一样，如Q learning（value based）用Q*在evaluate epsilon-greedy Q
on policy：采样策略和目标策略一样 如ppo（policy gradient） sarsa（value based）
图中可以看到Q-Learning 因为采用了opitmal 的 action-value function ，所以成为了off-policy，而一般on-policy如果用value function 或者 action-value function，不会用带星号（或者说optimal的）。
2、Q-Learning外其他算法如何得到策略网络？
最早，让强化学习在近几年火起来的便是DQN。都知道Q-Learning 只能用在离散动作，因为没有策略网络。
然而，不同于Q-Learning这一套boostrap的方法，Actor-Critic体系的方法如PPO、A2C、A3C根据策略梯度，自然而然学到了策略网络。其中A2C、A3C是直接的策略梯度，样本效率比较低，PPO算是在此基础上的利用重要性采样、梯度裁剪提高样本利用率。不用boostrap，就不会overestimate，导致有偏的估计，效果理论上更好。
策略梯度
不同于一个最常见的策略梯度更新公式如下：
θ
k
+
1
=
θ
k
+
α
?
θ
J
(
π
θ
)
∣
θ
k
\theta_{k+1}=\theta_k + \alpha\nabla_\theta J(\pi_\theta)|_{\theta_k}
θk+1?=θk?+α?θ?J(πθ?)∣θk??，其中
?
θ
J
(
π
θ
)
\nabla_\theta J(\pi_\theta)
?θ?J(πθ?)就是策略梯度。
为了让这一梯度可以被计算，需要转化为期望的形式，并且采样去估计这个期望，下面是进一步的推导：
?
θ
J
(
π
θ
)
=
E
τ
～
?
π
θ
[
R
(
τ
)
]
=
?
θ
∫
τ
P
(
τ
∣
θ
)
R
(
τ
)
=
∫
τ
?
θ
P
(
τ
∣
θ
)
R
(
τ
)
=
∫
τ
P
(
τ
∣
θ
)
?
θ
log
?
P
(
τ
∣
θ
)
R
(
τ
)
=
∫
τ
P
(
τ
∣
θ
)
?
θ
log
?
(
ρ
0
(
s
0
)
∏
t
=
0
T
P
(
s
t
+
1
∣
s
t
,
a
t
)
π
θ
(
a
t
∣
s
t
)
)
R
(
τ
)
=
∫
τ
P
(
τ
∣
θ
)
?
θ
log
?
(
∏
t
=
0
T
π
θ
(
a
t
∣
s
t
)
)
R
(
τ
)
=
E
τ
～
?
π
θ
[
∑
t
=
0
T
?
θ
log
?
π
θ
(
a
t
∣
s
t
)
R
(
τ
)
]
\nabla_\theta J(\pi_\theta) = \mathop{E} \limits_{\tau\sim\ \pi_{\theta}}\left[ R(\tau)\right ]\\ = \nabla_\theta \int_{\tau}P(\tau|\theta)R(\tau)\\ =\int_{\tau}\nabla_\theta P(\tau|\theta)R(\tau)\\ =\int_{\tau}P(\tau|\theta)\nabla_\theta \log P(\tau|\theta) R(\tau)\\ =\int_{\tau}P(\tau|\theta)\nabla_\theta \log \left(\rho_0(s_0) \prod_{t=0}^{T} P(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t) \right)R(\tau)\\ =\int_{\tau}P(\tau|\theta)\nabla_\theta \log \left(\prod_{t=0}^{T} \pi_\theta(a_t|s_t) \right)R(\tau)\\ =\mathop{E} \limits_{\tau\sim\ \pi_{\theta}}\left[\sum_{t=0}^{T}\nabla_\theta \log \pi_\theta(a_t|s_t) R(\tau)\right]\\
?θ?J(πθ?)=τ～?πθ?E?[R(τ)]=?θ?∫τ?P(τ∣θ)R(τ)=∫τ??θ?P(τ∣θ)R(τ)=∫τ?P(τ∣θ)?θ?logP(τ∣θ)R(τ)=∫τ?P(τ∣θ)?θ?log(ρ0?(s0?)t=0∏T?P(st+1?∣st?,at?)πθ?(at?∣st?))R(τ)=∫τ?P(τ∣θ)?θ?log(t=0∏T?πθ?(at?∣st?))R(τ)=τ～?πθ?E?[t=0∑T??θ?logπθ?(at?∣st?)R(τ)]
上面是最基础的策略梯度计算公式，围绕着
R
(
τ
)
R(\tau)
R(τ)这项有各种变体，常见的是去计算优势
?
θ
J
(
π
θ
)
=
E
τ
～
?
π
θ
[
∑
t
=
0
T
?
θ
log
?
π
θ
(
a
t
∣
s
t
)
A
π
θ
(
s
t
,
a
t
)
]
\nabla_\theta J(\pi_\theta) =\mathop{E} \limits_{\tau\sim\ \pi_{\theta}}\left[\sum_{t=0}^{T}\nabla_\theta \log \pi_\theta(a_t|s_t) A^{\pi_\theta}(s_t,a_t)\right]
?θ?J(πθ?)=τ～?πθ?E?[t=0∑T??θ?logπθ?(at?∣st?)Aπθ?(st?,at?)]
比如添加了baseline计算优势，并且不考虑过去的reward
? θ J ( π θ ) = E τ ～ ? π θ [ ∑ t = 0 T ? θ log ? π θ ( a t ∣ s t ) ( ∑ t ′ = t T R ( s t ′ , a t ′ , s t ′ + 1 ) ? b ( s t ) ) ] \nabla_\theta J(\pi_\theta) =\mathop{E} \limits_{\tau\sim\ \pi_{\theta}}\left[\sum_{t=0}^{T}\nabla_\theta \log \pi_\theta(a_t|s_t) \left( \sum_{t'=t}^{T}R(s_{t'},a_{t'},s_{t'+1}) - b(s_t) \right)\right] ?θ?J(πθ?)=τ～?πθ?E?[t=0∑T??θ?logπθ?(at?∣st?)(t′=t∑T?R(st′?,at′?,st′+1?)?b(st?))]
也有用GAE估计优势的
TRPO （on-policy）
TRPO和下面的PPO都是试图多次利用已有的数据来更新策略，TRPO利用KL散度约束新老策略差异度：
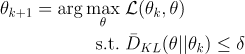
其中目标函数被称为代理优势函数
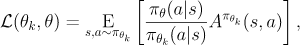
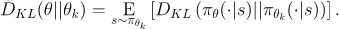
然后做泰勒展开近似（g就是代理又是函数）
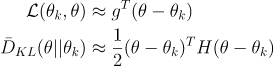
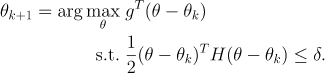
然后用拉格朗日对偶性求解，得到如下结果
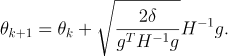
由于有近似，所以更新的时候需要回溯搜索
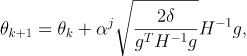
此外，
H
?
1
H^{-1}
H?1在实际的计算中很难做到，用共轭梯度法求解
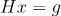
PPO（on-policy）
总的来说TRPO形式复杂，而PPO 用clip来约束差异，数学形式和计算更简洁，效果也很好。著名的OpenAI Five就是用的PPO
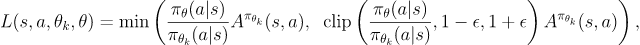
3、一些Q-Learning衍生出去的算法，如何“变”出一个策略网络呢？
那其他基于Q-Learning Booststrap体系的网络（off-policy的DDPG、offlineRL里的IQL、CQL）又该如何得到策略网络呢？下面简单介绍一下几种明显的DQN的衍生体。
DDPG（off-policy）
不同于最常见的随机策略的表达方式：
a
t
～
π
(
?
∣
s
t
)
a_t \sim \pi(\cdot|s_t)
at?～π(?∣st?)
DDPG采用确定策略梯度：
a
t
=
μ
(
s
t
)
a_t = \mu(s_t)
at?=μ(st?)
也就是说，当确定了最优动作价值函数
Q
?
(
s
,
a
)
Q^*(s,a)
Q?(s,a)，动作也被确定：
a
?
(
s
)
=
a
r
g
m
a
x
a
Q
?
(
s
,
a
)
a^*(s)=arg\mathop{max}\limits_{a}Q^*(s,a)
a?(s)=argamax?Q?(s,a)，从公式的形式来看，DDPG就是DQN在连续动作下的情况，DDPG也只能用在连续动作。
简单来说，DDPG就是把原来DQN的target，即
r
+
γ
m
a
x
a
′
Q
?
(
s
′
,
a
′
)
r + \gamma \mathop{max}\limits_{a'}Q^*(s',a')
r+γa′max?Q?(s′,a′)，改为
r
+
γ
Q
?
(
s
′
,
μ
(
s
′
)
)
r + \gamma Q^*(s',\mu(s'))
r+γQ?(s′,μ(s′))
对于拥有target network来减少overestimate的DQN，更新的目标就是对于
?
\phi
?最小化以下目标：
L
(
?
,
D
)
=
E
(
s
,
a
,
r
,
s
′
,
d
o
n
e
)
～
D
[
(
Q
?
(
s
,
a
)
?
(
r
+
γ
(
1
?
d
o
n
e
)
Q
?
t
a
r
g
e
t
(
s
′
,
μ
θ
t
a
r
g
e
t
(
s
′
)
)
)
)
2
]
L(\phi,\mathcal{D})=\mathop{E}\limits_{(s,a,r,s',done)\sim\mathcal{D}}\left[\left( Q_\phi(s,a)-\left(r + \gamma(1-done)Q_{\phi _{target}}(s',\mu_{\theta_{target}}(s'))\right) \right)^2 \right]
L(?,D)=(s,a,r,s′,done)～DE?[(Q??(s,a)?(r+γ(1?done)Q?target??(s′,μθtarget??(s′))))2]
相应的对于策略的更新就是对于
θ
\theta
θ最大化以下目标：
E
s
～
D
[
Q
?
(
s
,
μ
θ
(
s
)
)
]
\mathop{E}\limits_{s\sim \mathcal{D}}[Q_\phi(s,\mu_\theta(s))]
s～DE?[Q??(s,μθ?(s))]
其中target network按照如下更新：
?
t
a
r
g
e
t
=
ρ
?
t
a
r
g
e
t
+
(
1
?
ρ
)
?
θ
t
a
r
g
e
t
=
ρ
θ
t
a
r
g
e
t
+
(
1
?
ρ
)
θ
\phi_{target} = \rho \phi_{target} + (1-\rho)\phi\\ \theta_{target} = \rho \theta_{target} + (1-\rho)\theta
?target?=ρ?target?+(1?ρ)?θtarget?=ρθtarget?+(1?ρ)θ
TD3（Twin Delayed DDPG）
准确来说就是在DDPG的基础上延时去更新target network，并使用clipped double-Q等trick ，就是加强版的DDPG，没有应用场景上的变化
CQL（offlineRL 和后文关系不大）
暂时不写
IQL（offlineRL 和后文关系不大）
暂时不写
4、为什么Q-Learning不用类似重要性采样的操作：
因为最优贝尔曼等式右侧期望只与状态转移分布有关，和策略无关，理论上各种策略都可以迭代到 Q ? Q^* Q?
5、 同样是Actor-Critic体系的，都要用策略梯度，为什么比如SAC是off-policy，A2C/A3C/PPO是on-policy？
根据OpenAI里RL的教程，Model-Free RL可以根据学的内容大致分为 Policy Optimization（A2C/A3C/PPO ：on-policy） 和 Q-Learning （DQN：off-policy），以及两者的融合（DDPG、SAC，两者均为off-policy）。
至于Actor-Critic 体系，从最早的含义而言，需要Critic价值迭代，Actor策略迭代，广义上而言，有策略网络和价值网络的都算，我认为SAC和DDPG一样都属于后者，因为他们的策略网络是通过最大化价值函数而来的。
SAC（off-policy）
SAC可以粗略看为加了熵的DDPG，它引入了最大熵学习的概念，也就是在各个reward上加上
α
H
(
π
(
?
∣
s
t
)
)
\alpha H(\pi(\cdot|s_t))
αH(π(?∣st?))，其中
H
(
P
)
=
E
x
～
P
[
?
log
?
P
(
x
)
]
H(P) = \mathop{E}\limits_{x\sim P}\left[-\log P(x) \right]
H(P)=x～PE?[?logP(x)]
也就是说：
Q
π
(
s
,
a
)
=
E
s
′
～
P
,
a
′
～
π
[
R
(
s
,
a
,
s
′
)
+
γ
(
Q
π
(
s
′
,
a
′
)
+
α
H
(
π
(
?
∣
s
′
)
)
)
]
=
E
s
′
～
P
,
a
′
～
π
[
R
(
s
,
a
,
s
′
)
+
γ
(
Q
π
(
s
′
,
a
′
)
?
α
log
?
(
π
(
a
′
∣
s
′
)
)
)
]
Q^\pi(s,a) = \mathop{E}\limits_{s'\sim P,a'\sim \pi}\left[R(s,a,s')+\gamma (Q^\pi(s',a')+\alpha H(\pi(\cdot|s')))\right] \\ = \mathop{E}\limits_{s'\sim P,a'\sim \pi}\left[R(s,a,s')+\gamma (Q^\pi(s',a')-\alpha \log(\pi(a'|s')))\right]
Qπ(s,a)=s′～P,a′～πE?[R(s,a,s′)+γ(Qπ(s′,a′)+αH(π(?∣s′)))]=s′～P,a′～πE?[R(s,a,s′)+γ(Qπ(s′,a′)?αlog(π(a′∣s′)))]
和TD3比较相似的是SAC也用了boostraping的Q函数更新方法，以及target Q-network、clipped double-Q等手段
不一样的地方是除了引入最大熵，SAC的策略不需要target policy，而且是随机策略
SAC的Q更新部分， s , a , r , s ′ s,a,r,s' s,a,r,s′来自replay buffer， a ′ a' a′来自最新策略的采样：
Q π ( s , a ) ≈ E s ′ ～ P , a ′ ～ π [ r + γ ( Q π ( s ′ , a ~ ′ ) ? α log ? ( π ( a ~ ′ ∣ s ′ ) ) ) ] Q^\pi(s,a) \approx \mathop{E}\limits_{s'\sim P,a'\sim \pi}\left[r+\gamma (Q^\pi(s',\tilde{a}')-\alpha \log(\pi(\tilde{a}'|s')))\right] Qπ(s,a)≈s′～P,a′～πE?[r+γ(Qπ(s′,a~′)?αlog(π(a~′∣s′)))]
因为动作不是来自buffer，不是来自其他策略，所以也就没有重要性采样的说法
对于策略的学习，最大化
V
π
(
s
)
=
E
a
～
π
[
Q
π
(
s
,
a
)
?
α
log
?
π
(
a
∣
s
)
]
V^\pi(s)=\mathop{E}\limits_{a\sim\pi}[Q^\pi(s,a)-\alpha\log\pi(a|s)]
Vπ(s)=a～πE?[Qπ(s,a)?αlogπ(a∣s)]
借助重参数化手段
a ~ θ ( s , ξ ) = t a n h （ μ θ ( s ) + σ θ ( s ) ⊙ ξ ) , ξ ～ N ( 0 , I ) \tilde{a}_\theta(s,\xi)=tanh（\mu_\theta(s)+\sigma_\theta(s)\odot \xi), \xi\sim \mathcal{N}(0,I) a~θ?(s,ξ)=tanh（μθ?(s)+σθ?(s)⊙ξ),ξ～N(0,I)
得到
E
a
～
π
θ
[
Q
π
θ
(
s
,
a
)
?
α
log
?
π
θ
(
a
∣
s
)
]
=
E
ξ
～
N
[
Q
π
θ
(
s
,
a
~
θ
(
s
,
ξ
)
)
?
α
log
?
π
θ
(
a
~
θ
(
s
,
ξ
)
∣
s
)
]
\mathop{E}\limits_{a\sim\pi_\theta}[Q^{\pi_\theta}(s,a)-\alpha\log\pi_\theta(a|s)] = \mathop{E}\limits_{\xi\sim\mathcal{N}}[Q^{\pi_\theta}(s,\tilde{a}_\theta(s,\xi))-\alpha\log\pi_\theta(\tilde{a}_\theta(s,\xi)|s)]
a～πθ?E?[Qπθ?(s,a)?αlogπθ?(a∣s)]=ξ～NE?[Qπθ?(s,a~θ?(s,ξ))?αlogπθ?(a~θ?(s,ξ)∣s)]
进一步的double-Q不再展开
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Web缓存代理
- 【python_数据分组】
- 在做题中学习（34）：两整数之和（不准用运算符+）
- Swagger + Knife4j 接口文档的整合
- Navicat Premium连接阿里云数据库MySQL
- you may set `use_modular_headers!` globally in your Podfile, or specify `:modular_headers =＞ true`
- TS中断言、转换的应用
- 外汇天眼：芝加哥商品交易所（CME）对鹰七公司规定进行罚款
- ai智能语音机器人系统的话术怎样设置效果比较好
- 关于面试的一些建议