道路拆除的题解
目录
原题描述:
题目描述
A 国有?座城市,从?
?编号。
?号城市是 A 国的首都。城市间由?
?条双向道路连通,通过每一条道路所花费的时间均为?11?单位时间。
现在 A 国打算拆除一些不实用的道路以减小维护的开支,但 A 国也需要保证主要线路不受影响。因此 A 国希望道路拆除完毕后,利用剩余未被拆除的道路,从 A 国首都出发,能到达?号与?
?号城市,且所要花费的最短时间分别不超过?
??与?
?(注意这是两个独立的条件,互相之间没有关联,即不需要先到?
??再到
)。
A 国想请你帮他们算算,在满足上述条件的情况下,他们最多能拆除多少条道路。 若上述条件永远无法满足,则输出?。
输入格式
第一行两个正整数?,表示城市数与道路数。
接下来??行,每行两个正整数?
,表示一条连接?
?号点与?
?号点的道路。数据保证没有重边和自环。
最后一行四个整数,分别为??,??
,?
?,
,。
输出格式
仅一行一个整数,表示答案。
样例 #1
样例输入 #1
5 6
1 2
2 3
1 3
3 4
4 5
3 5
5 3 4 3样例输出 #1
3样例 #2
样例输入 #2
3 2
1 2
2 3
2 2 3 1样例输出 #2
-1提示
【数据范围】
对于??的数据,
;
另有??的数据,
;
另有??的数据,
;
对于?的数据,
。
【样例??解释】
拆除?三条边。
注意:不需要令首都与除了?外的点在拆除之后依然连通。
【样例??解释】
即使一条边都不拆除,首都到??号点的最短时间也都达到了?
?单位时间。
题目大意:
给你一个无向图,问你最少可以去掉多少条边,可以使1到的最短距离<=
,使1到
的最短距离<=
主要思路:
首先分析一下,如果想最短,那么一定是形如这样的形式。
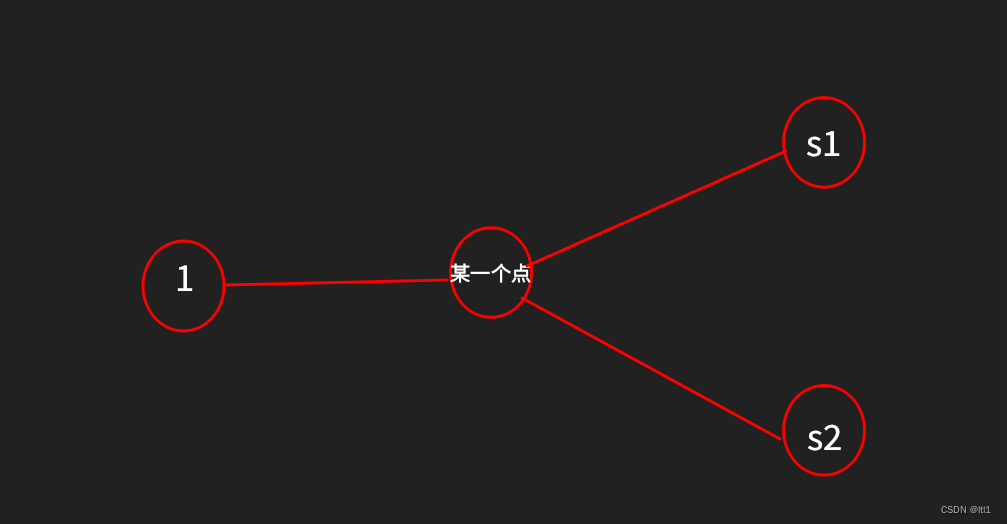
这样一定是最短的,那么我们就可以用一个dis数组来表示。
dis[3][3010]
dis[0][i]表示,从1走到i的最短路径。
dis[1][i]表示,从s1走到i的最短路径。
dis[2][i]表示,从s2走到i的最短路径。
那么当(dis[0][i]+dis[1][i]+dis[2][i])最小时且dis[0][i]+dis[1][i]<=t1,dis[0][i]+dis[2][i]<=t2。
m-(dis[0][i]+dis[1][i]+dis[2][i])就是答案了。
至于dis怎么求?
由于题目中说过,每条边的时间是1,就是边权为1,既然边权为1,那么可以用bfs求。
代码code:
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<vector<int>> v(3010);
int dis[10][3010];
int ans=0x3f3f3f3f;
void bfs(int x,int* tmpdis)//由于传数组,用指针
{
tmpdis[x] = 0;
queue<pair<int,int>> q;
q.push({x,0});
while(!q.empty())
{
int u=q.front().first,step=q.front().second;
q.pop();
for(auto it:v[u])
{
if(tmpdis[it] == 0x3f3f3f3f)
{
tmpdis[it] = step+1;
q.push({it,step+1});
}
}
}
//是不是很像最短路?
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v1;
cin>>u>>v1;
v[u].push_back(v1);
v[v1].push_back(u);
}
int s1,s2,t1,t2;
cin>>s1>>t1>>s2>>t2;
memset(dis,0x3f,sizeof(dis));//dis初始化
bfs(1,dis[0]);
bfs(s1,dis[1]);
bfs(s2,dis[2]);
//求三个dis。
for(int i=1;i<=n;i++)
{
if(dis[0][i]+dis[1][i]<=t1&&dis[0][i]+dis[2][i]<=t2)
{
ans = min(ans,dis[0][i]+dis[1][i]+dis[2][i]);//计算
}
}
cout<<(ans == 0x3f3f3f3f?-1:m-ans);//三目运算符,当无答案时,用-1
return 0;
}
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- QML —— CheckBox示例,嵌入TabView页中(附完整源码)
- 力扣hot100 删除链表的倒数第 N 个结点 快慢指针 递归回溯
- 生成随机id
- docker 安装
- 边缘计算AI智能盒子的视频源必须是固定点监控摄像头吗?
- 3dmax全景图用什么渲染 全景图云渲染使用教程
- PAT乙级1045 快速排序
- D55XT100-ASEMI电机专用整流桥D55XT100
- 基于web的亚热带常见自然林病虫害识别系统——开篇
- uniapp 字母索引列表插件(组件版) Ba-SortList