[ECE] 2.1 - 2.6 Number Systems, Operations

Decimal versus Binary Numbers

????????Decimal Numbers:?

Each digit takes a value btw 0~9, (decimal point)

????????????????Express the decimal number 47 as a sum of the values of each digit.

????????Binary Numbers:?

Each digit takes a value either 0 or 1, (Binary point)

? ? ? ? ? ? ? ? 0.1011 = 0.5 + 0.125 + 0.0625 = 0.6875

? ? ? ? ? ? ? ? MSB：Most? Significant Bit?

????????????????????????The left-most bit is the MSB (most significant bit); its weight depends on the size of the binary number.

????????????????LSB ：Least Significant Bit?

????????????????????????The right-most bit is the LSB (least significant bit) in a binary whole number and has a weight of 20 = 1.

????????????????1. What is the largest decimal number that can be represented in binary with eight bits?

? ? ? ? ? ? ? ? ?A:?255 = 2^8 - 1

Repeated Division-by-2 Method

A systematic method of converting whole numbers from decimal to binary is the repeated division-by-2 process.?For example, to convert the decimal number 12 to binary, begin by dividing 12 by 2. Then divide each resulting quotient by 2 until there is a 0 whole-number quotient. The remainders generated by each division form the binary number.

? ? ? ? ? ? ? ??

?Converting Decimal Fractions to Binary

1.?Sum-of-Weights:?

0.625 = 0.5 + 0.125 = 2^-1 + 2^-3 = 0.101

2.?Repeated Multiplication by 2

For example, to convert the decimal fraction 0.3125 to binary, begin by multiplying 0.3125 by 2 and then multiplying each resulting fractional part of the product by 2 until the fractional product is zero or until the desired number of decimal places is reached. The carry digits, or carries, generated by the multiplications produce the binary number. The first carry produced is the MSB, and the last carry is the LSB. This procedure is illustrated as follows

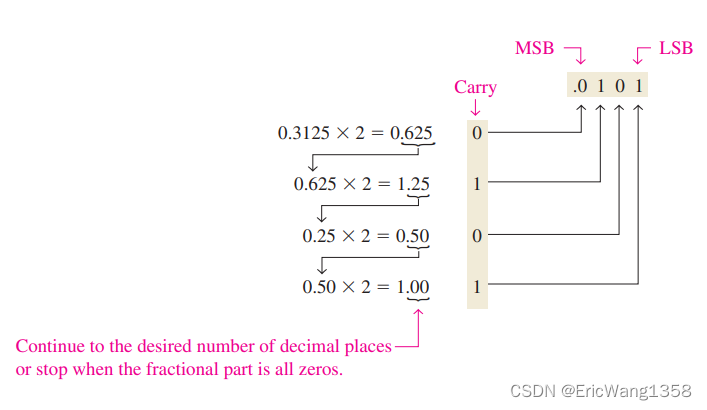
?( 0.625 's carry is 0, 1.25's carry is 1 ）( carry here means "进位” )

Binary Arithmetic

To understand digital systems, you must know the basics of binary addition, substraction, multiplication, and division. This section provides an introduction that will be expanded in later sections.

Binary Addition

0 + 0 = 0 Sum of 0 with a carry of 0

0 + 1 = 1 Sum of 1 with a carry of 0

1 + 0 = 1 Sum of 1 with a carry of 0

1 + 1 = 10 Sum of 0 with a carry of 1

When binary numbers are added, the last condition creates a sum of 0 in a given column and a carry of 1 over to the next column to the left.?When there is a carry of 1, you have a situation in which three bits are being added (a bit in each of the two numbers and a carry bit).

Binary Subtraction

0 - 0 = 0

1 - 1 = 0

1 - 0 = 1

10 - 1 = 1 (0 - 1 with a borrow of 1)

Binary Multiplication

0 * 0 = 0

0 * 1 = 0

1 * 0 = 0

1 * 1 = 1

Binary Division

Division in binary follows the same procedure as division in decimal

Complements of Binary Numbers

The 1’s complement and the 2’s complement of a binary number are important because they permit the representation of negative numbers. The method of 2’s complement arithmetic is commonly used in computers to handle negative numbers.

Finding the 1’s Complement

The 1’s complement of a binary number is found by changing all 1s to 0s and all 0s to 1s.

The simplest way to obtain the 1’s complement of a binary number with a digital circuit is to use parallel inverters (NOT circuits).?

Finding the 2’s Complement

First Method

The 2’s complement of a binary number is found by adding 1 to the LSB of the 1’s complement.

?2's complement = (1's complement) + 1

?An alternative method

Another method of finding the 2’s complement of a binary number is as follows:

1. Start at the right with the LSB and write the bits as they are up to and including the first 1.

2. Take the 1’s complements of the remaining bits

?The 2’s complement of a negative binary number can be realized using inverters and an adder

Signed Numbers

Digital systems, such as the computer, must be able to handle both positive and negative numbers. A signed binary number consists of both sign and magnitude information.

There are three forms in which signed integer (whole) numbers can be represented in binary: sign-magnitude, 1’s complement, and 2’s complement. Of these, the 2’s complement is the most important and the sign-magnitude is the least used. Noninteger and very large or small numbers can be expressed in floating-point format.

The Sign Bit

The left-most bit in a signed binary number is the sign bit, which tells you whether the number is positive or negative.

A 0 sign bit indicates a positive number, and a 1 sign bit indicates a negative number

Sign-Magnitude Form

The left-most bit is the sign bit and the remaining bits are the magnitude bits.

Notice that the only difference between +25 and 225 is the sign bit because the magnitude bits are in true binary for both positive and negative numbers.

(In the sign-magnitude form, a negative number has the same magnitude bits as the corresponding positive number but the sign bit is a 1 rather than a zero.)

1’s Complement Form

In the 1’s complement form, a negative number is the 1’s complement of the corresponding positive number

2’s Complement Form

In the 2’s complement form, a negative number is the 2’s complement of the corresponding positive number

Negative numbers are the 2’s complements of the corresponding positive numbers.

Infonote

Processors use the 2’s complement for negative integer numbers in arithmetic operations. The reason is that subtraction of a number is the same as adding the 2’s complement of the number. Processors form the 2’s complement by inverting the bits and adding 1, using special instructions that produce the same result as the adder

The Decimal Value of Signed Numbers

Decimal values of positive and negative numbers in the sign-magnitude form are determined by summing the weights in all the magnitude bit positions where there are 1s and ignoring those positions where there are zeros. The sign is determined by examination of the sign bit

Decimal values of positive numbers in the 1’s complement form are determined by summing the weights in all bit positions where there are 1s and ignoring those positions where there are zeros. Decimal values of negative numbers are determined by assigning a negative value to the weight of the sign bit, summing all the weights where there are 1s, and adding 1 to the result.

Decimal values of positive and negative numbers in the 2’s complement form are determined by summing the weights in all bit positions where there are 1s and ignoring those positions where there are zeros. The weight of the sign bit in a negative number is given a negative value.

?

The 1’s complement system requires adding 1 to the summation of weights for negative numbers but not for positive numbers. Also, the 1’s complement form is generally not used because two representations of zero (00000000 or 11111111) are possible.

Range of Signed Integer Numbers

We have used 8-bit numbers for illustration because the 8-bit grouping is common in most computers and has been given the special name byte.

The formula for finding the number of different combinations of n bits is

Total combinations = 2^n

For 2’s complement signed numbers, the range of values for n-bit numbers is

Range = -(2^(n-1) ) to +(2^(n-1) - 1)