单位圆内接三角形的角是外接三角
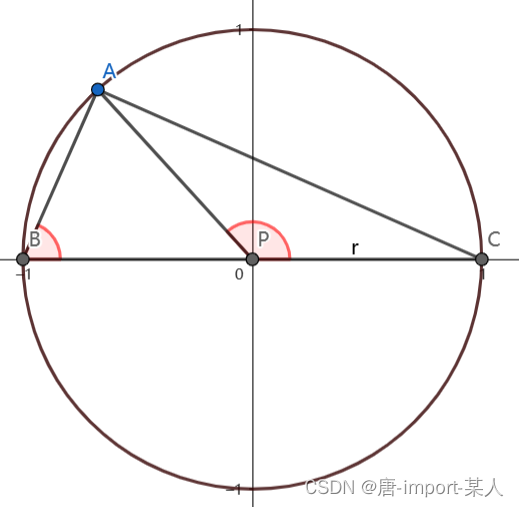
证明
∠
A
P
C
=
2
∠
A
B
C
∠APC=2∠ABC
∠APC=2∠ABC
∴
∴
∴ 三角形内角和为180
$∵
\begin{cases}
∠ABP+∠BAP+∠APB=180
\∠ABC+∠BAC+∠ACB=180
\∠PAC+∠PCA+∠APC=180
\end{cases}
$
∴
A
P
=
B
P
=
P
C
=
r
∴AP=BP=PC=r
∴AP=BP=PC=r
∵
∵
∵△PAB和△PAC为等腰三角形
∴
∴
∴等腰三角形两底角相等
∵
∠
A
B
C
=
∠
B
A
P
=
∠
①
,
∠
P
A
C
=
∠
P
C
A
=
∠
②
∵∠ABC=∠BAP=∠①,∠PAC=∠PCA=∠②
∵∠ABC=∠BAP=∠①,∠PAC=∠PCA=∠②
∵
∵
∵ 线段BP在线段BC上
∴
∠
A
B
P
=
∠
A
B
C
=
∠
①
∴∠ABP=∠ABC=∠①
∴∠ABP=∠ABC=∠①
$∵
\begin{cases}
2∠①+∠APB=180
\∠①+∠②+∠BAC=180
\2∠②+∠APC=180
\end{cases}
$
∴
单位圆所对圆周角
90
°
∴单位圆所对圆周角90°
∴单位圆所对圆周角90°
∵
∠
B
A
C
=
90
°
∵∠BAC=90°
∵∠BAC=90°
$∵
\begin{cases}
2∠①+∠APB=180
\∠①+∠②=90
\2∠②+∠APC=180
\end{cases}
$
∵
2
∠
(
90
°
?
∠
①
+
∠
A
P
C
=
180
∵2∠(90°-∠①+∠APC=180
∵2∠(90°?∠①+∠APC=180
∵
180
°
?
2
∠
①
+
∠
A
P
C
=
180
∵180°-2∠①+∠APC=180
∵180°?2∠①+∠APC=180
∵
∠
A
P
C
=
2
∠
①
∵∠APC=2∠①
∵∠APC=2∠①
∵ ∠ A P C = 2 ∠ A B C ∵∠APC=2∠ABC ∵∠APC=2∠ABC
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 芯课堂 | 华芯微特段码屏驱动
- 128.最长连续序列
- 四、UART_阻塞发送&中断接收
- LangChain 69 向量数据库Pinecone入门
- Rust-析构函数
- 通付盾获2023年度移动互联网APP产品安全漏洞治理优秀案例 荣获工信部CAPPVD漏洞库技术支撑单位
- Java云腾内部管理系统(源码+开题)
- pip vs conda
- 今日冬至|数九寒天,御寒保暖从脚开始
- 使用css实现 Typora markdown 标题自动编号