PaddlePaddle飞桨（学习笔记二——Tensor张量）

目录

1、Tensor的创建

1.1指定数据创建

1.2指定形状创建

1.3指定区间创建

1.4指定对象创建

1.4.1 Tensor对象

?1.4.2 Image对象

1.5自动创建

2、Tensor 的属性

2.1 Tensor 的形状（shape）

2.2 Tensor 的数据类型（dtype）

2.3 Tensor 的设备位置（place）

2.4 Tensor 的名称（name）

3、Tensor 的操作

3.1 索引和切片

3.2 赋值与修改

3.3Tensor广播

---

1、Tensor的创建

1.1指定数据创建

与 Numpy 创建数组方式类似，通过给定 Python 序列（如列表 list、元组 tuple），可使用?paddle.to_tensor?创建任意维度的 Tensor。

#创建一维Tensor
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])

#创建二维Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
#创建三维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])

?ndim_3_Tensor的输出

Tensor(shape=[2, 2, 5], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[[1 , 2 , 3 , 4 , 5 ],
         [6 , 7 , 8 , 9 , 10]],

        [[11, 12, 13, 14, 15],
         [16, 17, 18, 19, 20]]])

三个张量的可视化?

?

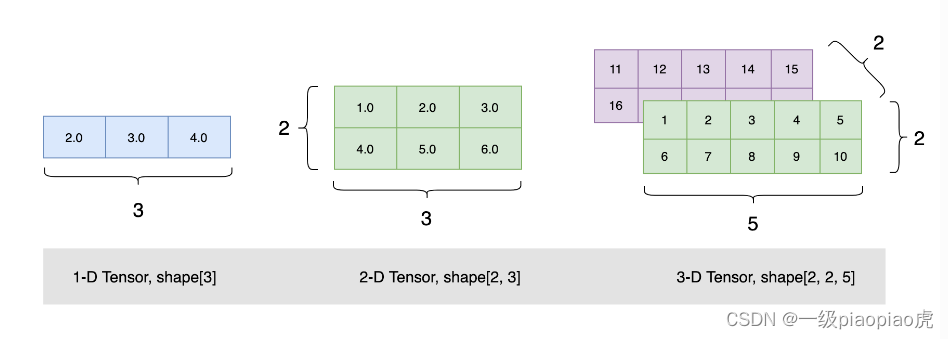
1.2指定形状创建

如果要创建一个指定形状的 Tensor，可以使用?paddle.zeros、paddle.ones、paddle.full?实现。

paddle.zeros([m, n])             # 创建数据全为 0，形状为 [m, n] 的 Tensor
paddle.ones([m, n])              # 创建数据全为 1，形状为 [m, n] 的 Tensor
paddle.full([m, n], 10)          # 创建数据全为 10，形状为 [m, n] 的Tensor
paddle.empty(shape=[3, 2])       # 创建数据全为 1，形状为 [3, 2] 的Tensor

?

1.3指定区间创建

?如果要在指定区间内创建 Tensor，可以使用paddle.arange、?paddle.linspace?实现。

paddle.arange(start, end, step)  
# 创建以步长 step 均匀分隔区间[start, end)的 Tensor
paddle.linspace(start, stop, num) 
# 创建以元素个数 num 均匀分隔区间[start, stop)的 Tensor

?

1.4指定对象创建

1.4.1 Tensor对象

• 创建一个与其他 Tensor 具有相同 shape 与 dtype 的 Tensor，可通过?paddle.ones_like?、?paddle.zeros_like?、?paddle.full_like?、paddle.empty_like?实现
• 拷贝并创建一个与其他 Tensor 完全相同的 Tensor，可通过?paddle.clone?实现。

y = paddle.ones_like(x)

y = paddle.clone(x)

• 创建一个满足特定分布的 Tensor，如?paddle.rand,?paddle.randn?,?paddle.randint?等。

#服从均匀分布的、范围在[low, high)的随机 Tensor，形状为 shape
out1 = paddle.randint(low=-5, high=5, shape=[2, 3])

#符合均匀分布的、范围在[0, 1)的 Tensor，形状为 shape
out1 = paddle.rand(shape=[2, 3])

#符合标准正态分布的随机 Tensor，形状为 shape
out1 = paddle.randn(shape=[2, 3])

• 通过设置随机种子创建 Tensor，可每次生成相同元素值的随机数 Tensor，可通过?paddle.seed?和?paddle.rand?组合实现。

?1.4.2 Image对象

• 对于图像场景，可使用?paddle.vision.transforms.ToTensor?直接将 PIL.Image 格式的数据转为 Tensor，使用?paddle.to_tensor?将图像的标签（Label，通常是 Python 或 Numpy 格式的数据）转为 Tensor。

• 对于文本场景，需将文本数据解码为数字后，再通过?paddle.to_tensor?转为 Tensor。不同文本任务标签形式不一样，有的任务标签也是文本，有的则是数字，均需最终通过 paddle.to_tensor 转为 Tensor。

from PIL import Image
import paddle
import paddle.vision.transforms as T
import paddle.vision.transforms.functional as F

img_arr = ((paddle.rand((4, 5, 3)) * 255.).astype('uint8')).numpy()
fake_img = Image.fromarray(img_arr)
#将形状为 （H x W x C）的输入数据 
#PIL.Image 或 numpy.ndarray 转换为 (C x H x W)
transform = T.ToTensor()
tensor = transform(fake_img)

?

1.5自动创建

除了手动创建 Tensor 外，实际在飞桨框架中有一些 API 封装了 Tensor 创建的操作，从而无需用户手动创建 Tensor。

2、Tensor 的属性

2.1 Tensor 的形状（shape）

形状是 Tensor 的一个重要的基础属性，可以通过?Tensor.shape?查看一个 Tensor 的形状，以下为相关概念：

• shape：描述了 Tensor 每个维度上元素的数量。

• ndim： Tensor 的维度数量，例如向量的维度为 1，矩阵的维度为 2，Tensor 可以有任意数量的维度。

• axis 或者 dimension：Tensor 的轴，即某个特定的维度。

• size：Tensor 中全部元素的个数。

ndim_4_Tensor = paddle.ones([2, 3, 4, 5])



print("Data Type of every element:", ndim_4_Tensor.dtype)
print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])

?

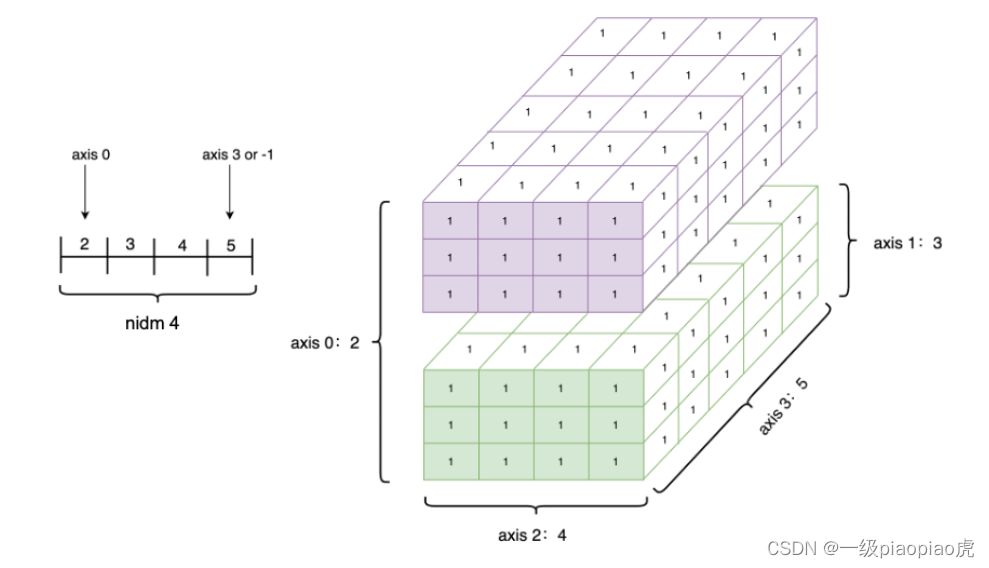
?重置 Tensor 形状（Reshape） 的方法

在指定新的 shape 时存在一些技巧：

• -1?表示这个维度的值是从 Tensor 的元素总数和剩余维度自动推断出来的。因此，有且只有一个维度可以被设置为 -1。

• 0?表示该维度的元素数量与原值相同，因此 shape 中 0 的索引值必须小于 Tensor 的维度（索引值从 0 开始计，如第 1 维的索引值是 0，第二维的索引值是 1）。

x = paddle.to_tensor([1, 2, 3])
y = paddle.reshape(x, [1, 3])


origin:[3, 2, 5] reshape:[3, 10]      actual: [3, 10] 
# 直接指定目标 shape
origin:[3, 2, 5] reshape:[-1]         actual: [30] 
# 转换为 1 维，维度根据元素总数推断出来是 3*2*5=30
origin:[3, 2, 5] reshape:[-1, 5]      actual: [6, 5] 
# 转换为 2 维，固定一个维度 5，另一个维度根据元素总数推断出来是 30÷5=6
origin:[3, 2, 5] reshape:[0, -1]      actual: [3, 10] 
# reshape:[0, -1]中 0 的索引值为 0，按照规则，转换后第 0 维的元素数量与
#原始 Tensor 第 0 维的元素数量相同，为 3；第 1 维的元素数量根据元素总值
#计算得出为 30÷3=10。
origin:[3, 2]    reshape:[3, 1, 0]    error： 
# reshape:[3, 1, 0]中 0 的索引值为 2，但原 Tensor 只有 2 维，无法找到与
#第 3 维对应的元素数量，因此出错。

说明：

除了 paddle.reshape 可重置 Tensor 的形状，还可通过如下方法改变 shape：

• paddle.squeeze，可实现 Tensor 的降维操作，即把 Tensor 中尺寸为 1 的维度删除。

• paddle.unsqueeze，可实现 Tensor 的升维操作，即向 Tensor 中某个位置插入尺寸为 1 的维度。

• paddle.flatten，将 Tensor 的数据在指定的连续维度上展平。

• paddle.transpose，对 Tensor 的数据进行重排。

原位（Inplace）操作和非原位操作的区别

飞桨框架的 API 有原位（Inplace）操作和非原位操作之分，原位操作即在原 Tensor 上保存操作结果，输出 Tensor 将与输入 Tensor 共享数据，并且没有 Tensor 数据拷贝的过程。非原位操作则不会修改原 Tensor，而是返回一个新的 Tensor。通过 API 名称区分两者，如?paddle.reshape?是非原位操作，paddle.reshape_?是原位操作。

2.2 Tensor 的数据类型（dtype）

Tensor 的数据类型 dtype 可以通过?Tensor.dtype?查看，支持类型包括：bool、float16、float32、float64、uint8、int8、int16、int32、int64、complex64、complex128。

同一 Tensor 中所有元素的数据类型均相同，通常通过如下方式指定：

• 通过给定 Python 序列创建的 Tensor，可直接使用 dtype 参数指定。如果未指定：

  • 对于 Python 整型数据，默认会创建?int64?型 Tensor；

  • 对于 Python 浮点型数据，默认会创建?float32?型 Tensor，并且可以通过?paddle.set_default_dtype?来调整浮点型数据的默认类型。

修改数据类型的方法

飞桨框架提供了paddle.cast?接口来改变 Tensor 的 dtype：

float64_Tensor = paddle.cast(float32_Tensor, dtype='float64')

2.3 Tensor 的设备位置（place）

#创建 CPU 上的 Tensor
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
print(cpu_Tensor.place)

#创建 GPU 上的 Tensor
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print(gpu_Tensor.place) # 显示 Tensor 位于 GPU 设备的第 0 张显卡上

#创建固定内存上的 Tensor
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print(pin_memory_Tensor.place)

2.4 Tensor 的名称（name）

print("Tensor name:", paddle.to_tensor(1).name)

3、Tensor 的操作

3.1 索引和切片

通过索引或切片方式可访问或修改 Tensor。飞桨框架使用标准的 Python 索引规则与 Numpy 索引规则，与?Indexing a list or a string in Python?类似。具有以下特点：

1. 基于 0-n 的下标进行索引，如果下标为负数，则从尾部开始计算。

2. 通过冒号?:?分隔切片参数，start:stop:step?来进行切片操作，其中 start、stop、step 均可缺省。

3.2 赋值与修改

请慎重通过索引或切片修改 Tensor，该操作会原地修改该 Tensor 的数值，且原值不会被保存。如果被修改的 Tensor 参与梯度计算，仅会使用修改后的数值，这可能会给梯度计算引入风险。飞桨框架会自动检测不当的原位（inplace）使用并报错。

import numpy as np

x = paddle.to_tensor(np.ones((2, 3)).astype(np.float32)) # [[1., 1., 1.], [1., 1., 1.]]

x[0] = 0                      # x : [[0., 0., 0.], [1., 1., 1.]]
x[0:1] = 2.1                  # x : [[2.09999990, 2.09999990, 2.09999990], [1., 1., 1.]]
x[...] = 3                    # x : [[3., 3., 3.], [3., 3., 3.]]

x[0:1] = np.array([1,2,3])    # x : [[1., 2., 3.], [3., 3., 3.]]

x[1] = paddle.ones([3])       # x : [[1., 2., 3.], [1., 1., 1.]]

3.3Tensor广播

飞桨 Tensor 的广播机制主要遵循如下规则（参考?Numpy 广播机制）：

• 每个 Tensor 至少为一维 Tensor。

• 从最后一个维度向前开始比较两个 Tensor 的形状，需要满足如下条件才能进行广播：两个 Tensor 的维度大小相等；或者其中一个 Tensor 的维度等于 1；或者其中一个 Tensor 的维度不存在。

# 可以广播的例子 2
x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从最后一个维度向前依次比较：
# 第一次：y 的维度大小是 1
# 第二次：x 的维度大小是 1
# 第三次：x 和 y 的维度大小相等
# 第四次：y 的维度不存在
# 所以 x 和 y 是可以广播的
z = x + y
print(z.shape)
# [2, 3, 4, 5]

在了解两个 Tensor 在什么情况下可以广播的规则后，两个 Tensor 进行广播后的结果 Tensor 的形状计算规则如下：

• 如果两个 Tensor 的形状的长度不一致，会在较小长度的形状矩阵前部添加 1，直到两个 Tensor 的形状长度相等。

• 保证两个 Tensor 形状相等之后，每个维度上的结果维度就是当前维度上的较大值。

举例如下：

x = paddle.ones((2, 1, 4))
y = paddle.ones((3, 1)) # y 的形状长度为 2，小于 x 的形状长度 3，因此会在 y 的形状前部添加 1，结果就是 y 的形状变为[1, 3, 1]
z = x + y
print(z.shape)
# z 的形状: [2,3,4]，z 的每一维度上的尺寸，将取 x 和 y 对应维度上尺寸的较大值，如第 0 维 x 的尺寸为 2，y 的尺寸为 1，则 z 的第 0 维尺寸为 2

?

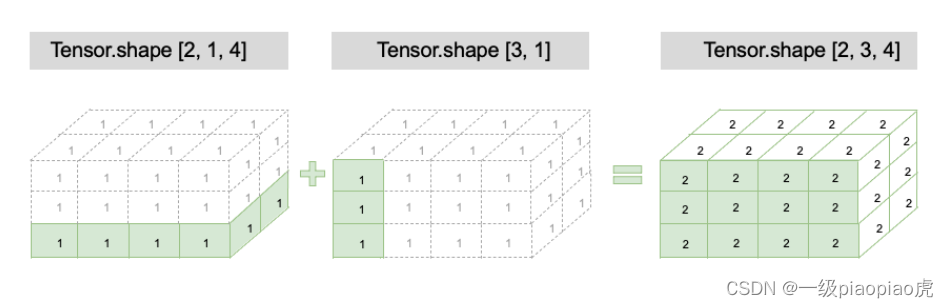
3.4Tensor运算

x.abs()                       #逐元素取绝对值
x.ceil()                      #逐元素向上取整
x.floor()                     #逐元素向下取整
x.round()                     #逐元素四舍五入
x.exp()                       #逐元素计算自然常数为底的指数
x.log()                       #逐元素计算 x 的自然对数
x.reciprocal()                #逐元素求倒数
x.square()                    #逐元素计算平方
x.sqrt()                      #逐元素计算平方根
x.sin()                       #逐元素计算正弦
x.cos()                       #逐元素计算余弦
x.add(y)                      #逐元素相加
x.subtract(y)                 #逐元素相减
x.multiply(y)                 #逐元素相乘
x.divide(y)                   #逐元素相除
x.mod(y)                      #逐元素相除并取余
x.pow(y)                      #逐元素幂运算
x.max()                       #指定维度上元素最大值，默认为全部维度
x.min()                       #指定维度上元素最小值，默认为全部维度
x.prod()                      #指定维度上元素累乘，默认为全部维度
x.sum()                       #指定维度上元素的和，默认为全部维度


x + y  -> x.add(y)            #逐元素相加
x - y  -> x.subtract(y)       #逐元素相减
x * y  -> x.multiply(y)       #逐元素相乘
x / y  -> x.divide(y)         #逐元素相除
x % y  -> x.mod(y)            #逐元素相除并取余
x ** y -> x.pow(y)            #逐元素幂运算


x.isfinite()                  
#判断 Tensor 中元素是否是有限的数字，即不包括 inf 与 nan
x.equal_all(y)                
#判断两个 Tensor 的全部元素是否相等，并返回形状为[]的布尔类 0-D Tensor
x.equal(y)                    
#判断两个 Tensor 的每个元素是否相等，并返回形状相同的布尔类 Tensor
x.not_equal(y)                
#判断两个 Tensor 的每个元素是否不相等
x.less_than(y)                
#判断 Tensor x 的元素是否小于 Tensor y 的对应元素
x.less_equal(y)               
#判断 Tensor x 的元素是否小于或等于 Tensor y 的对应元素
x.greater_than(y)             
#判断 Tensor x 的元素是否大于 Tensor y 的对应元素
x.greater_equal(y)            
#判断 Tensor x 的元素是否大于或等于 Tensor y 的对应元素
x.allclose(y)                 
#判断 Tensor x 的全部元素是否与 Tensor y 的全部元素接近，并返回形状为[]的布尔类 0-D Tensor