2024/1/20 并查集

目录

并查集关键代码

亲戚

村村通

团伙（新知识）

---

并查集关键代码

返回祖宗节点+路径压缩：

int find(int x)
{
    if(f[x]!=x) f[x]=find(f[x]);
    return f[x];
}

合并：

void make(int x,int y)
{
    int f1=find(f[x]);
    int f2=find(f[y]);
    if(f1!=f2)
    {
        f[f1]=f2;
    }
}

亲戚

P1551 亲戚 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：这道题用并查集，首先输入数据，进行初始化。

如果是亲戚，就合并他们（make(int x,int y)）

最后判断输入的两个数据是否返回同一个祖宗节点，如果是，则输出YES；反之输出NO。

完整代码

#include <bits/stdc++.h>
int n,m,p;
const int N = 5050;
int f[N];
int find(int x)
{
    if(f[x]!=x) f[x]=find(f[x]);
    return f[x];
}
void make(int x,int y)
{
    int f1=find(f[x]);
    int f2=find(f[y]);
    if(f1!=f2)
    {
        f[f1]=f2;
    }
}
int main()
{
    std::cin >> n >> m >> p;
    for(int i = 1;i <= n;i ++)
    {
        f[i]=i;
    }
    while(m --)
    {
        int x,y;
        std::cin >> x >> y;
        make(x,y);
    }
    while(p --)
    {
        int x,y;
        std::cin >> x >> y;
        int x1=find(x);
        int y1=find(y);
        if(x1==y1)
        {
            std::cout<<"Yes\n";
        }
        else
            std::cout<<"No\n";
    }
    return 0;
}

村村通

P1536 村村通 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：这道题用并查集，两个村庄之间每修一条路，需要修的路的条数就减少一条，最后输出还需要修的道路条数。

常识：有n个村庄，那么需要修的道路条数为n-1。

错误代码：

void make(int x,int y)
{
    int f1=find(x);
    int f2=find(y);
    if(f1!=f2)
    {
        p[f1]=f2;
    }
    ans--;
}

?

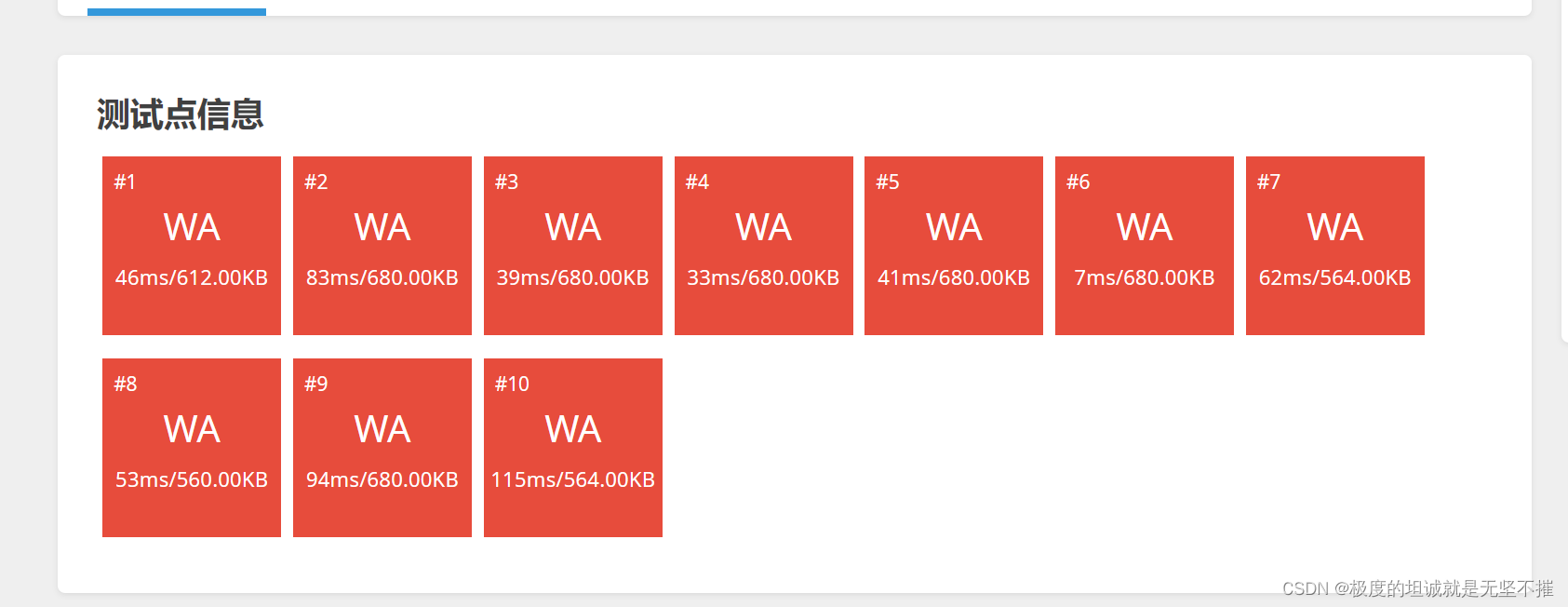ans--不应该在外面，要在if里面

如果他们祖宗节点不一样才要减一，意味着这两个村庄连接需要修一条路，一样的话就表示可以联通，答案就不用相减了

AC代码：

#include <bits/stdc++.h>
const int N = 1010;
int p[N];
int ans;
int find(int x)
{
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
void make(int x,int y)
{
    int f1=find(x);
    int f2=find(y);
    if(f1!=f2)
    {
        p[f1]=f2;
        ans--;
    }
}
int main()
{
    int n,m;
    while(std::cin >> n >> m)
    {
        if(n==0)
        {
            return 0;
        }
        ans=n-1;
        for(int i = 1;i <= n;i ++)
        {
            p[i]=i;
        }
        for(int i = 1;i <= m;i ++)
        {
            int x,y;
            std::cin >> x >> y;
            find(x);
            find(y);
            make(x,y);
        }
        std::cout<<ans<<"\n";
    }
    return 0;
}

团伙（新知识）

P1892 [BOI2003] 团伙 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

思路：并查集+反集

关于反集

完整代码

#include <bits/stdc++.h>
const int N = 5050*2;
int f[N];
int ans;
int find(int x)
{
    if(f[x]!=x) f[x]=find(f[x]);
    return f[x];
}
void make(int x,int y)
{
    int f1=find(x);
    int f2=find(y);
    if(f1!=f2)
    {
        f[f1]=f2;
    }
}
int main()
{
    int n,m;
    std::cin >> n >> m;
    for(int i = 1;i <= 2*n;i ++)
    {
        f[i]=i;
    }
    for(int i = 1;i <= m;i ++)
    {
        std::string s;
        int p,q;
        std::cin >> s >> p >> q;
        if(s=="F")
        {
            find(p),find(q);
            make(p,q);
        }
        else if(s=="E")
        {
            find(p+n),find(q);//反集合合并
            make(p+n,q);
            find(q+n),find(p);
            make(q+n,p);
        }
    }
    for(int i = 1;i <= n;i ++)
    {
        if(f[i]==i)
            ans++;
    }
    std::cout<<ans;
    return 0;
}

?