用于噪声和分段相位测量的鲁棒相位展开算法（全文翻译-2区Optics Express）

摘要：本文提出了一种在存在噪声和分段相位的情况下进行相位展开的鲁棒相位展开算法（RPUA）。RPUA方法提出了一种新的相位导数模型，结合纠错迭代来实现抗噪声效果。此外，它使用数值载波频率和条纹外推法在空间域中桥接相位岛，从而消除高度误差，从而能够解决分段相位展开问题。通过数值模拟和与三种传统方法的比较，证明了RPUA的高鲁棒性和高效性。此外，三个实验表明，RPUA可以准确地获得不同噪声下的展开相位，并具有处理分段相位的能力，具有可靠的实用性。

1. 导言

相位解包裹是通过消除包裹相位（通常由反正切函数产生）中的模糊性来获取真正的解包裹相位的过程[1]。它是许多干涉测量应用中必不可少的程序，例如干涉测量、数字全息[2]、合成孔径雷达成像（SAR）[3,4]、磁共振成像（MRI）[5]和轮廓测量[6]。 然而，在实际应用中，相位解包很难在存在噪声或孤立区域的情况下实现。在过去几十年中，人们开发了许多相位解包方法，这些方法通常可分为路径跟踪法[7-19]、最小规范法[20-31]和其他方法[32-39]。路径跟踪方法利用相位残差或相位质量图来寻找合适的路径，然后沿选定的路径对模数 2 映射包裹的相位差进行线积分，以避免误差的累积[1]。 这些方法可以获得精确的解，但容易受到相位噪声或相位残留的影响，因为包裹相位中的严重噪声会影响其可靠性。相比之下，最小正则算法构建了包裹相位梯度与解包裹相位梯度之差的评估函数，并通过优化该函数获得稳健的解包裹相位。 为完成这一任务，人们提出了许多方法，包括基于最小平方（LS）的算法[20-26]、基于强度方程传输（TIE）或快速傅立叶变换（FFT）的算法[27-31]。最小正则算法效率高，且由于与路径无关，在一定程度上不受相位噪声的影响，通常可以从噪声包裹相位中获得平滑的非包裹相位，已被广泛应用。此外，最小正则算法基于相邻像素间相位导数的绝对值小于 n 的假设，这意味着包裹相位差是真实的梯度场[1]。 然而，严重的相位噪声（如电子斑点噪声）可能会使这一假设失效，因为高噪声可能会导致相邻像素之间的相位差超出包裹相位的 2n 跳变区域，从而带来较大的解包裹误差。然而，滤波方法可能会抹去一些相位跳跃或有用信息，而且很多方法都很耗时。

上述方法适用于相位整体连续的解决方案，但在实际应用中，部分反射镜会出现遮挡或破损。 "例如，在组装好的望远镜系统中，多个主镜或副镜通常会被 "蜘蛛 "支撑结构部分覆盖[40]。除了相位噪声，相位解包也会受到这些相位岛的影响，从而导致较大误差。 因此，在对整个测量区域进行解包时，相位岛之间的不连续性是一个挑战。此外，它不仅可能造成相位岛内部的误差，还可能造成相位岛之间的高度（活塞）故障。 目前采用的方法是填充缺失区域的坡度数据，以获得连续的局部坡度，具体方法是计算曲面图两个方向的差值[40]。

本文提出了一种鲁棒相位解包算法（RPUA）来解决有噪声或分段相位的全局相位解包问题。所提方法的鲁棒性主要包括两个方面：一是构建一个新的相位导数模型，结合最小平方法和纠错迭代来实现抗噪声相位解包。本文的其余部分安排如下：第 2 节描述了所提出的方法；第 3 节介绍了数值分析和仿真，并与几种有代表性的方法进行了比较；第 4 节讨论了所提出的方法在激光干涉测量、斑点干涉测量和分段相位测量中的实际应用；最后，第 5 节得出了结论。

2.提出了鲁棒相位展开算法

2.1。相位导数的新模型展开相位φ（x，y）和包裹相位ξ（x，y）之间的关系，取模2π，在π到-π的范围内，可以写成

其中k（x，y）是待确定的整数。假设包裹相位的相位导数与真实相位的相位衍生物相同，则可以通过建立以下泊松方程来计算展开相位：

其中ρ（x，y）是泊松方程的输入。一般的做法是计算二阶导数以恢复原始相位。

在没有噪声的情况下执行上述计算。噪声的存在会在有噪声和无噪声的相位导数之间产生误差，这使相位展开变得复杂。实现鲁棒展开相位的关键是使有噪声相位的相位导数接近无噪声相位的导数。在这里，我们提出了一个新的相位导数模型,实现抗噪声相位展开：

其中2是拉普拉斯算子，sin（·）是正弦函数，为了便于描述，省略了（x，y）。

在不失一般性的情况下，分析从无噪声阶段开始。当不受噪声影响时，包裹的相位是连续的（除了2个π跳点），这意味着相位导数很小。对于这些无噪声点，可以应用一阶近似

由于相导数的值很小，通常小于 at，因此除了 2t 跳变点外，传统模型也能得到类似的结果：

?

其中W是被包裹的运算符。方程(4)和(5)表明，所提出的模型与无噪声点的传统模型近似等效

?

如下面所讨论的，可以通过迭代来消除微小的近似误差。

当相位受到严重噪声的干扰时，包裹的相位变得不连续。有噪声点的相位导数比无噪声点的要大得多。在传统的模型中，这些噪声点被视为相位导数中的相位跳跃，并在相位展开中产生大的误差。然而，对于所提出的模型，我们可以很容易地获得：

可以发现，所有值大于无噪声点的噪声点的相位导数都设置在-1到1的范围内。与传统型号相比，我们

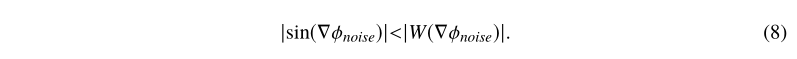
而且不难找到

上述分析表明，在不受噪声影响的情况下，所提出的模型具有与传统模型相似的相位导数，而对于噪声严重的相位，它可以使噪声相位导数更接近无噪声相位的相位导数。为了说明两个模型之间的差异，图1显示了从图6（a1）第3节的x方向中间一行提取的两个不同相位导数的图。图1（a）显示，在没有噪声的情况下，这两个曲线图在很大程度上重合。当引入严重的相位噪声时，如图1（b）所示，传统模型包含大量的高相位跳变，这些跳变是由于噪声相位导数的大值而产生的。相反，所提出的方法减少了噪声的相位跳跃。传统方法和建议方法的标准偏差分别为1.249拉德和0.514拉德，对应于等式（9）。

2.2近似误差校正的迭代

方程（3）中输入的泊松方程的离散形式为

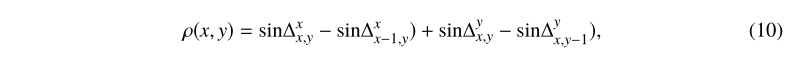
其中，sin?xx，y和sin?y x，y分别是包裹相的x和y方向上的差异，定义为

其中M和N分别是相对于x和y索引的网格点的数量。使用离散余弦变换（DCT）方法来计算展开相位，展开相位可以如下所示..

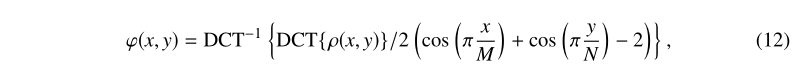
?其中：

其中Round是舍入运算，Φn（x，y）定义为：

其中ψn（x，y）是第n次迭代中计算的展开相位，<·>是平均运算。方程（14b）可以校正展开相位和包裹相位之间的相位差。

第n次迭代的相位误差定义为

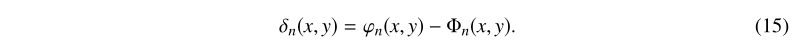
因为Φn（x，y）是通过最小二乘法计算的展开相位；它是连续的，这意味着当相位跳跃发生在校正的相位φn（x，y）中时，相应的相位跳跃也发生在相位误差δn（x、y）中。因此，如果ψn（x，y）中存在误差，则可以假设φn（x、y）具有近似误差或不完全校正相位。随后，δn（x，y）可以是下一次迭代的输入包裹相位，以获得ψ_n+1（x，y），并代入等式。（13）和（14）以再次校正未包裹相位。

当δn（x，y）中没有展开误差时，φn（x、y）可以被视为完全展开并等于真实相位。收敛条件设置为

其中ε和Nit分别是预定的收敛阈值和迭代次数。所提出的RPUA的迭代过程流程如图所示。2。

2.3.分段相位展开

图3（a）显示了望远镜系统中主反射镜的同时相移干涉图，显示了一个完整的反射镜被“蜘蛛”支撑结构划分为多个相岛。用传统相位展开算法计算的反射镜的展开相位如图所示。第3（b）段表明，随机高度误差发生在应处于相同高度的相位岛之间，导致相位展开失败

我们建议通过利用数值载波频率和条纹外推法在空间域中桥接分段相位来解决分段相位的相位展开，如图所示.

将数字载波频率添加到包裹相位

?其中T（x，y）是数字载波频率，可以写成:

其中α、β和γ是载波频率系数。我们获得了用ξT（x，y）再生干涉图IT

增加数字载波频率以增加干涉图中的条纹数，使相岛边缘的结构特征更加明显，这有助于以提高下面的条纹外推法的精度。添加的数字载波频率也应满足奈奎斯特采样定理.

分段相位展开的困难在于相位岛之间没有任何连接。RPUA利用相位岛的数据将条纹外推到被遮挡的部分。对我们获得的再生干涉图进行条纹外推法

其中Ext｛·｝是条纹外推算子。外推的条纹可能不完全符合遮挡区域的相位分布，但这并不重要。通过该步骤建立分段相位的连接。外推干涉图具有所有网格点的数据，其中可以应用单帧傅立叶变换方法来检索相位

其中，F（·）是傅立叶变换，Fs是正一阶边带高斯滤波器，Arg（·）为计算相位角的函数，PU{·}为所提出的相位导数模型的相位展开。因为使用了正的一阶边带，所以噪声对相位恢复的影响最小。

此后，从检索到的相位中减去相加的数字载波频率，以获得完整的相位

然而，φCOM（x，y）不是最终的真实相位，因为傅立叶变换在相位岛中可能仍然存在小误差，这将在模拟中说明。使用计算的相位φCOM（x，y）获得校正的整数

然后可以获得最终的展开相位

3.数值模拟与分析

?3.1近似误差的修正

当抑制噪声时，RPUA方法在无噪声点，特别是具有大相位梯度的点上产生近似误差。迭代的应用减少了噪声的影响以及近似误差。在迭代过程中，近似误差随着相位误差δn（x，y）收敛到阈值而减小，这使得展开相位接近无噪声相位。

通过数值模拟验证了RPUA的可行性。使用MATLAB内置函数峰值生成初始相位。为了直接显示差异，传统模型和RPUA的无噪声包裹相位的x方向上的中间一行相位导数的图如图所示。第5（a1）-（a6）段。在这里，我们使用峰值系数来显示初始相（PVinit）的峰谷变化。随着PVinit的增加，RPUA在具有大相位梯度的点上的近似误差也增加。当峰的系数设置为30（PVinit=439.175rad）时，两相导数非常不同。图5（b1）-（b6）显示了两个模型在相同迭代收敛条件下的迭代结果。很明显，传统的模型（蓝线）可以准确有效地获得解包裹的相位，并且RPUA也可以通过一次或两次以上的迭代来获得相同的结果动态范围大，传统的模型不可靠，难以获得正确的展开相位。相比之下，RPUA方法在计算的准确性和效率方面与小PVinit保持一致。结果表明，与传统模型相比，RPUA方法可以通过迭代来解决近似误差，并且具有更大的PVinit动态范围。

3.2、存在噪声时的相位展开

为了证明RPUA的抗噪声性能，将不同级别的噪声添加到相位中，并与几种常见的相位展开算法进行比较，这些算法包括迭代最小二乘相位展开（ILS）[21]、基于非连续路径可靠性排序的相位展开（SRNCP）[13]和基于傅立叶变换的快速PU（FPU）[28]。

迭代的收敛条件为ε=10?5，Nit=500。噪声为高斯噪声，噪声的标准偏差（σ噪声）设置为从低到高。随后，使用不同的方法对有噪声的包裹相位进行解包裹，并计算每种方法的残差，如图所示。6。结果表明，在低噪声条件下，四种方法的相位展开精度较高；然而，随着噪声水平的增加，ILS和SRNCP的精度都降低了。特别是，在严重的噪声下，它们的结果会出现明显的展开误差。与FPU相比，如图6（e3）和（e4）所示，RPUA在严重噪声下具有更好的PU结果。对于图6（g3）和（g4），残差的标准偏差分别为0.340和0.270 rad。

迭代的收敛条件为ε=10?5，Nit=500。噪声为高斯噪声，噪声的标准偏差（σ噪声）设置为从低到高。随后，使用不同的方法对有噪声的包裹相位进行解包裹，并计算每种方法的残差，如图所示。6。结果表明，在低噪声条件下，四种方法的相位展开精度较高；然而，随着噪声水平的增加，ILS和SRNCP的精度都降低了。特别是，在严重的噪声下，它们的结果会出现明显的展开误差。与FPU相比，如图6（e3）和（e4）所示，RPUA在严重噪声下具有更好的PU结果。对于图6（g3）和（g4），残差的标准偏差分别为0.340和0.270 rad。

此外，当引入严重噪声时，如图8所示，ILS、SRNCP和FPU方法不足以获得大的展开时令人满意的展开相位

?图6。四种方法在不同噪声水平下的未包络结果和相应残差。（a1）-（a3）是噪声包裹相位，（b1）-（g1）表示ILS，（b2）-（g2）表示SRNCP，（b3）-（g3）表示FPU，（b4）-（g 4）表示RPUA

即使使用较小的PVinit，它们的残差也会出现错误。然而，RPUA仍然能够成功完成相位展开，并获得良好的展开相位，如图8（b4）-7（g4）所示，残差的标准偏差分别为0.255、0.275和0.304 rad。

为了更全面地比较不同的方法，我们量化了每种方法的相位残差。如果残差的计算标准偏差小于10?5 rad，则将其设置为0，这表明展开相位与理论真实相位非常相似。定量结果总结在表1中，其中Mnoise是最大噪声值。

为了更直接地观察相位残差，残差的标准偏差与不同噪声水平的关系如图所示。第9（a）段，峰值系数设置为9（PVinit=131.914rad）。曲线图表明，ILS和SRNCP方法容易受到噪声的影响，并且噪声水平的增加导致展开性能的快速下降。

FPU方法在很大程度上不受噪声变化的影响，但由于PVinit较高，因此展开精度较低，这一点从图中可以明显看出。第7（e3）、7（g3）、8（e3。

图 7. 当标准导数为 0.6 rad 时，四种方法在不同 PVinit 下的解包结果。噪声的标准导数设为 0.6 rad。(a1)-(a3) 表示包裹相位，(b1)-(g1) 表示 ILS、(b2)-(g2) 表示 SRNCP，(b3)-(g3) 表示 FPU，(b4)-(g4) 表示 RPUA。

图9（b）显示了不同方法的计算精度与PVinit的关系图，噪声的标准导数设置为0.6 rad。很明显，初始相位PV的增加对其他三种方法有很大影响，而RPUA方法的展开精度变化最小。此外，所有定量结果都验证了当初始相位具有严重噪声、大PV或两者时，RPUA对抗噪声相位展开具有高鲁棒性。

3.3.计算时间

除了展开精度外，计算成本也是评估PU算法的一个重要指标。使用MATLAB在配备Intel Core i7-7700HQ CPU（2.80-GHz）和16GB RAM的笔记本电脑上进行计算。表2显示了当峰值系数设置为9（PVinit=131.914rad）时，具有不同噪声水平的不同方法的计算时间。

为了更直接地比较它们，计算时间如图10所示。从表2和图10可以看出，ILS的时间消耗最短，并且计算SRNCP和FPU的效率相对较低。此外，在存在低和中等噪声水平的情况下，RPUA的消耗时间非常接近ILS的消耗时间。然而，当相位被严重的噪声占据时，ILS无法获得可靠的展开相位，而RPUA在确保展开精度的同时仍然具有良好的效率。因此，RPUA在高噪声下具有令人满意的计算效率，提高了其实用性。3.4复杂噪声下的相位展开

3.4.在复噪声条件下的相位展开将散斑噪声加入到初始相位中，以进一步验证RPUA在抗噪声相位展开方面的性能。散斑噪声是使用线性模型以一个像素的平均大小生成的，如参考文献所述。[41]。峰的系数被设置为10（PVinit＝146.572拉德）。首先生成包含散斑噪声的包裹相位，然后添加其标准导数集为0.9rad的加性高斯噪声。四种方法的展开结果如图11所示。从残差和残差的直方图可以明显看出，只有RPUA才能获得连续的展开相位

?

在高复杂噪声下，其他三种方法的结果都存在较大的展开误差。四种方法的相应标准导数分别为7.364、10.771、1.477和0.569rad，这证明了在存在复杂噪声的情况下，RPUA对相位展开的鲁棒性。

3.5.分段相位展开

为了证明RPUA在分段相位展开上的优势，我们使用Zernike系数模拟了望远镜系统中传统主镜的相位，如表3所示，并手动添加了“蜘蛛”掩模。包裹阶段如图12（a）所示。四种方法的展开相位如图所示。12（b1）-12（b4），可以发现ILS、SRNCP和RPUA在每个相位岛内都有正确的展开相位，除了FPUA有明显误差。此外，残差如图所示。12（c1）-12（c4）表明ILS和SRNCP在相位岛之间引入了高度差。RPUA恢复的展开相位是连续的，并且与理论真实相位一致

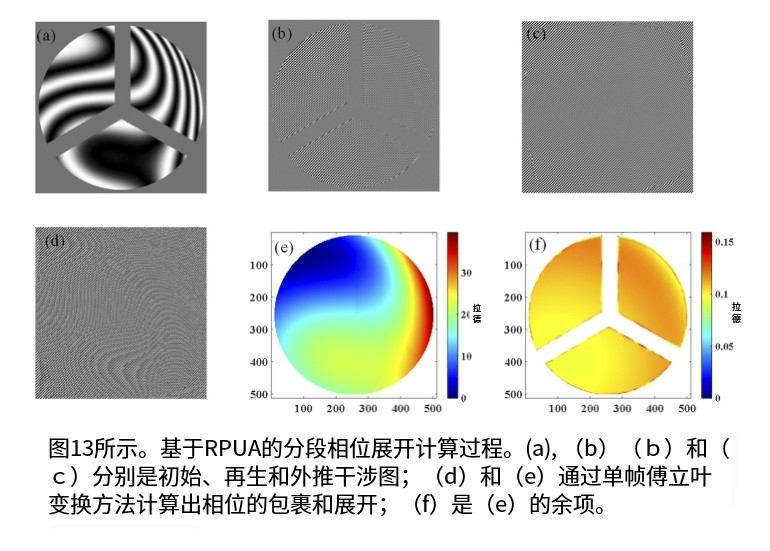
图13显示了RPUA的计算过程，其中图13（a）、13（b）和13（c）分别显示了初始干涉图、再生干涉图和外推干涉图。通过单帧傅立叶变换检索的包裹相位如图所示。13（d）和图13（e）显示了展开相位。很明显，分段的相位被连接为一个完整的相位，并且原始出现的区域被填充。然而，计算的结果通过傅立叶变换不能被视为最终阶段。如图中的残差所示。13（f），在相位岛的边缘处存在误差，应使用等式（22）对其进行校正，以获得真实相位。

?

随后，我们将标准导数集为0.7rad的高斯噪声添加到分割的相位中，并使掩模更加复杂，以增加相位岛的数量。不同方法的展开结果如图所示。14。很明显，高噪声的存在以及相位岛的数量和面积的增加导致ILS、SRNCP和FPU的相位岛内部出现大的相位展开误差。相岛之间的高度断层也被观察到更为严重。相反，所提出的RPUA方法不受相位岛数量和面积变化的影响，仍然可以实现抗噪声相位展开。

4.实验结果

4.1带噪声实验阶段的RPUA

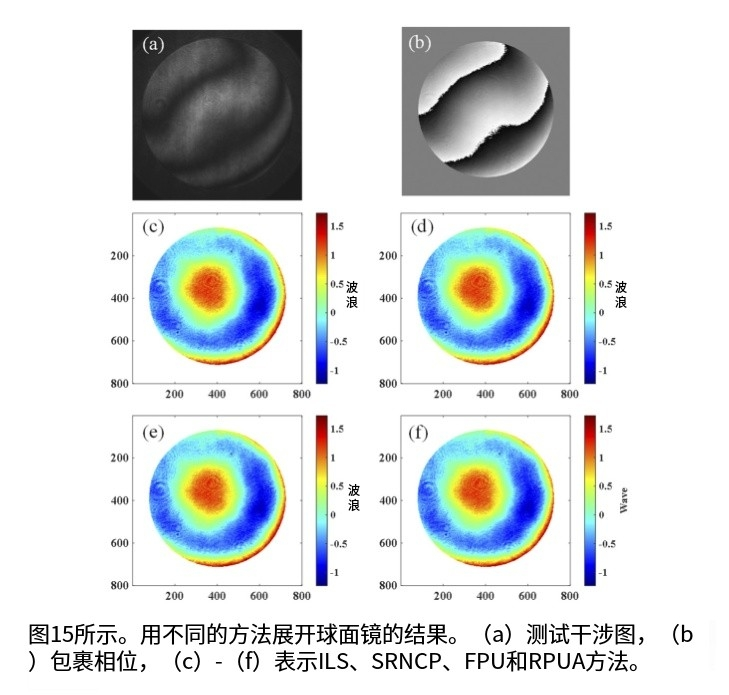
在第一次实验中，测量了一个球面镜，为了避免测试过程中的环境干扰，根据参考文献[42]采用了动态干涉测量方案，得到的干涉图如图 15（a）所示，使用双通相位解调方法得到的相位如图 15（b）所示。 (此外，ILS、SRNCP、FPU 和 RPUA 的计算时间分别为 1.829、13.309、3.147 和 1.683 s。

第二个实验根据参考文献[43]，利用斑点干涉测量法测量了粗糙平面的平面外变形。图 16（a）和图 16（b）显示了得到的干涉图和计算出的包裹相位，其中包裹相位受到严重斑点噪声的干扰。 图 16(c)-(f)所示为解包相位，其中 ILS、SRNCP 和 FPU 在达到收敛条件时仍存在较大的解包误差，增加迭代次数对结果的改善微乎其微。

4.2.分段相位测量的RPUA

在第三个实验中，将带有蜘蛛型掩模的球面镜添加到反射镜中。实验使用了根据参考文献1的同步相移动态干涉测量法。

?

相移干涉图和包裹相位如图17（a）和（b）所示。使用上述四种方法进行相位展开，如图17（c1）-（f1）所示。很明显，ILS、SRNCP和FPU的结果中出现了不可忽视的高度差。相反，RPUA的展开相位在相位岛之间具有连续的过剩，并且相位看起来更完整。为了更直接地观察这一点，我们为每种方法的展开相位的第300行（红点线）和第300列（蓝点线）绘制相位图，如图所示。17（c2）-（f2）。这表明其他三种方法的蓝线和红线都有明显的不连续性，并且高度差与测量相位的PV在一个数量级，表明它们的结果误差很大。相比之下，RPUA的两个图是平滑的，它们之间没有高度差，这更符合

参考文献：YI ZONG, MINGLIANG DUAN, CAIYUN YU, AND JIANXIN LI*?Robust phase unwrapping algorithm for noisy and segmented phase measurements?Nanjing University of Science and Technology, 2021