文献分享二：A Versatile Bias Control for Any-Point Locking in Lithium Niobate Mach–Zehnder Modulators

文献来源——Wang, L. L. and T. Kowalcyzk (2010). "A Versatile Bias Control Technique for Any-Point Locking in Lithium Niobate Mach–Zehnder Modulators." Journal of Lightwave Technology 28(11): 1703-1706.

一、前言

主要参考的是有两种偏置方法，有光功率监测法和加入抖动谐波置零信号的方法。

光功率监测的方法的反馈信号受输入功率电平波动和光路损耗的影响比较大，如果反馈量里边噪声比较大而原本输出的信号跟噪声接近的时候，或者光器件可靠性差，那么这种方法就没有意义了。所以此方法仅在实验室中出现的比较多，实际应用并没有使用过这种方法。

抖动信号的方法虽然用途更广泛一些，更加的稳定可靠，但是它不可以将偏置点锁定在调制曲线的任意位置，它的判定位置的方法是这样的：例如，在偏置电压上面给到一个抖动信号，如果锁定到调制曲线的1/4的位置，那么二次谐波为0，如果锁定在最小点，那么谐波的基波为零。并且，抖动信号相当于噪声，本身也会影响输出信号。

鉴于以上两种方法，本文章提出了基于抖动信号的可以把偏置点锁定在任意位置的方法。

二、基本原理

首先在输入偏置电压的时候加上一个低频信号（1KHZ左右），然后取出来输出端口的信号的一次和二次谐波，把二次谐波和基波的比值作为参考的反馈信号，这样可以得到与功率无关且单调性好的传递函数曲线，把偏置点锁定在任意位置。

公式推导如下:

首先输入输出光功率的表示如下：

里面的Δ由以下公式构成，同时考虑了失配引起的相位偏移

? ?代入得：

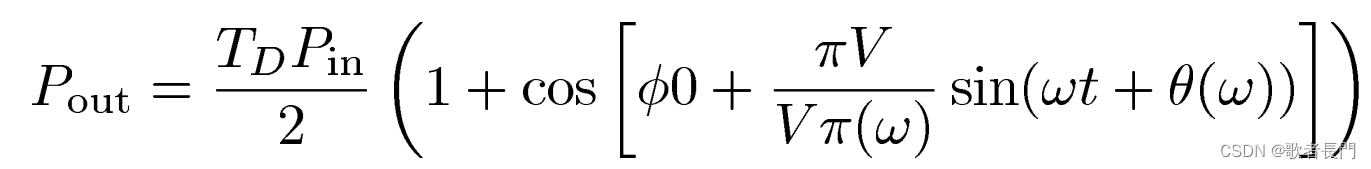
因为cosin前面的比例系数远小于1，先记作a，再三角展开：

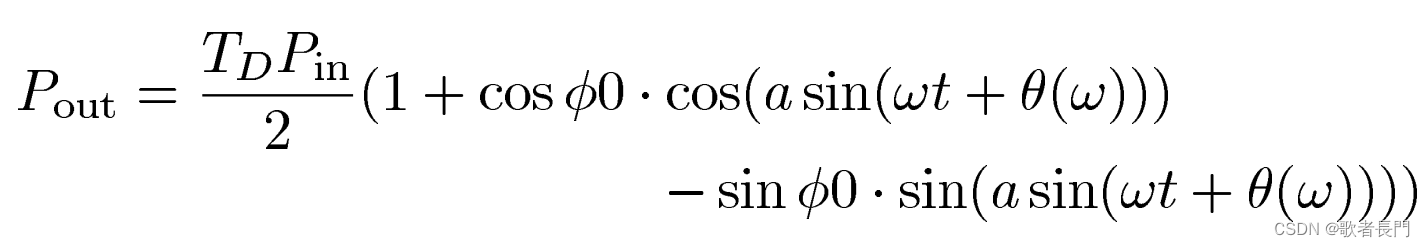
对含有抖动信号的三角函数项进行泰勒展开得：

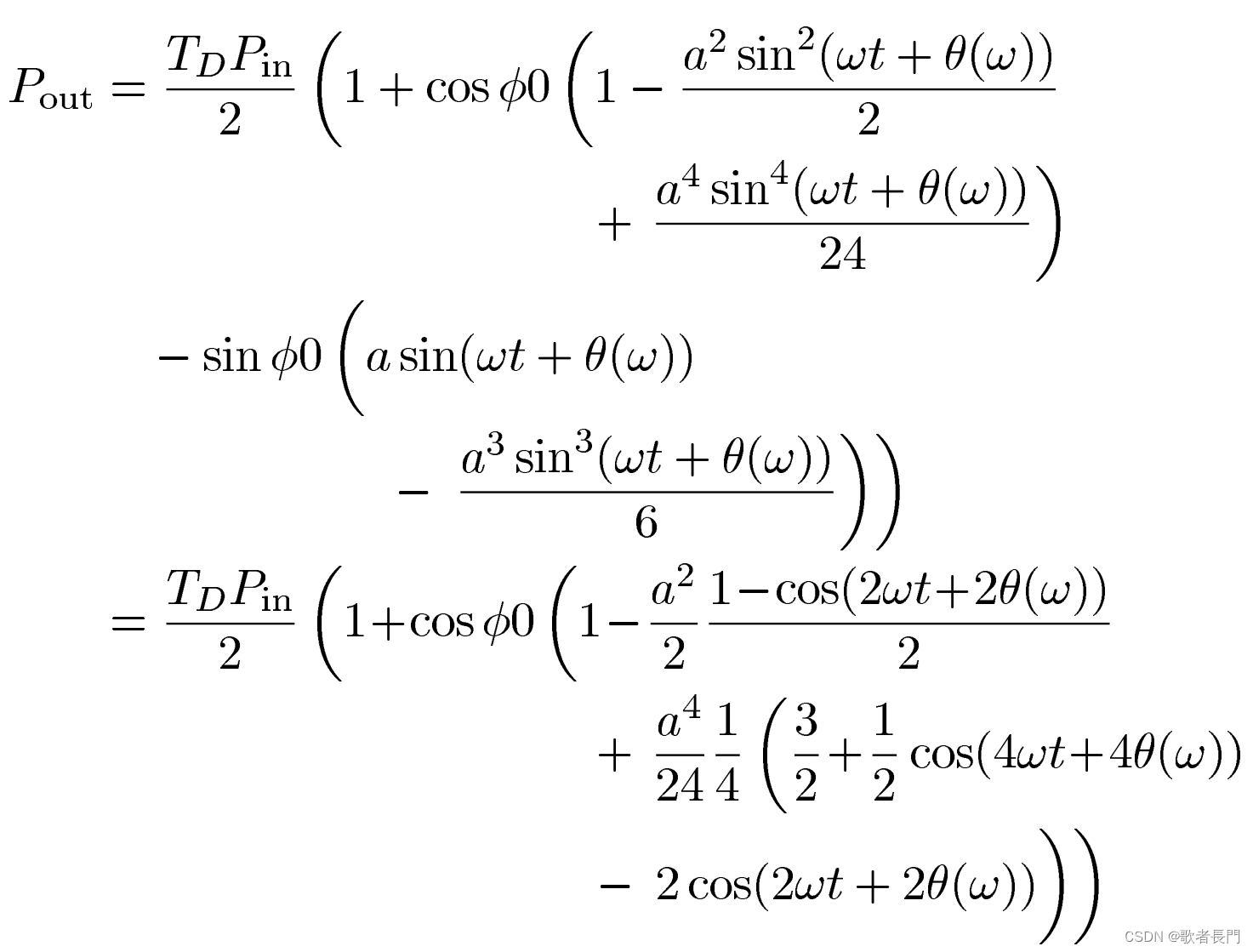
得出一次和二次谐波，并用R表示他们之间的比值：

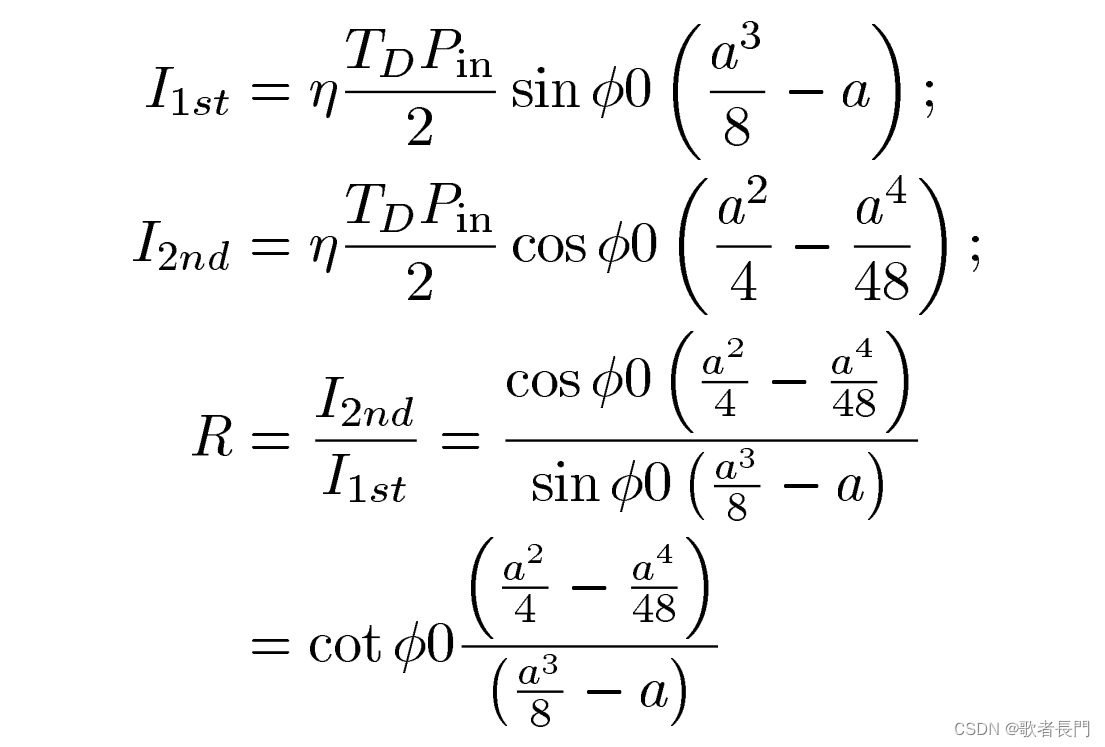
由上图公式可知，R与输入功率，MZM调制器得系数、光电二极管和调制效率都没有关系，只与直流偏置、半波电压或者说插入损耗有关。那么当我这个系统是确定的，并且抖动信号也是一个固定值时候，可以保证比值R与输入光功率无关。

通过对1kHZ1V信号仿真，得出12次谐波和MZM直流偏压相角的关系（红色实线），显然有很好的单调性：

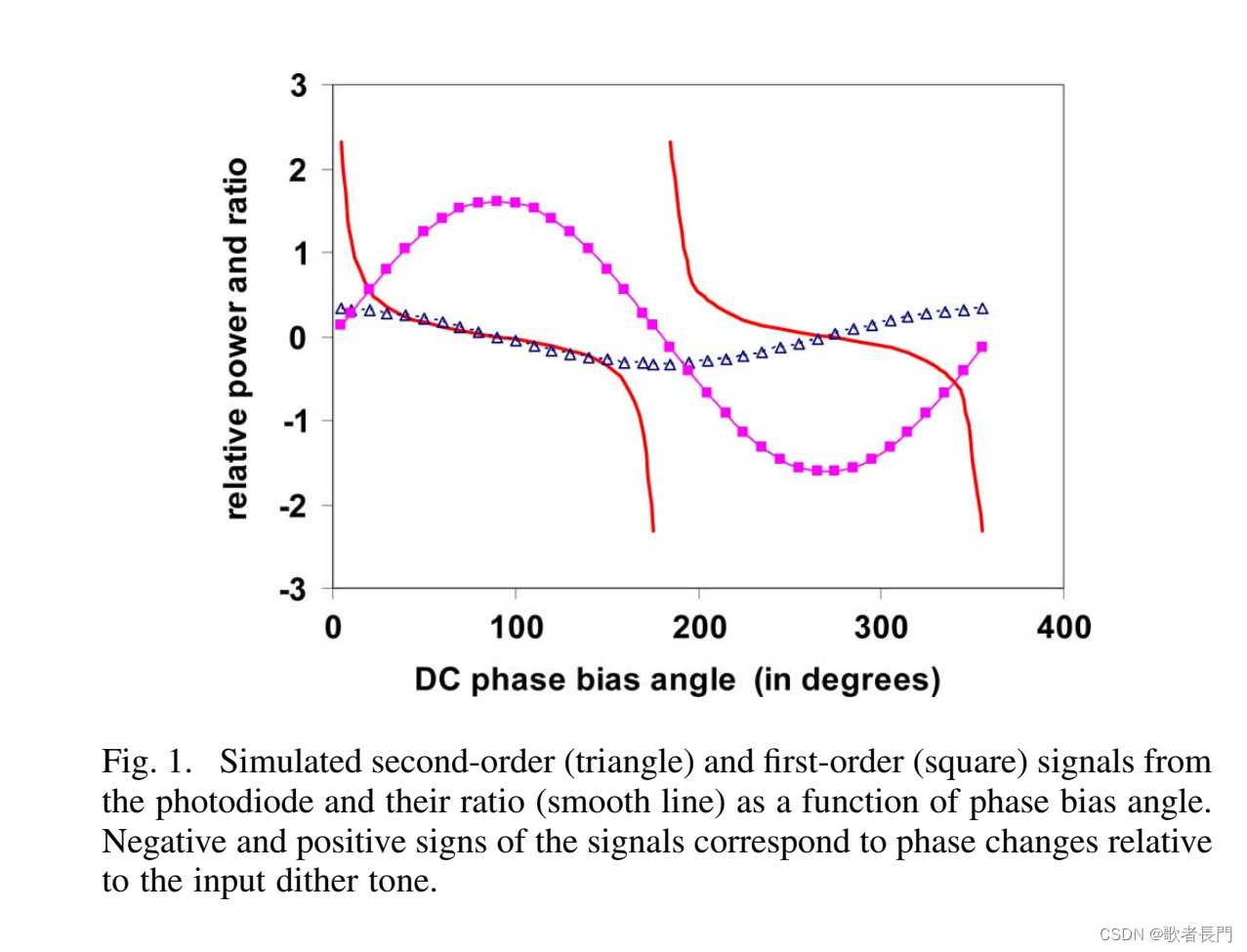
三、实验验证与结论

设计得偏置控制器得如图所示：

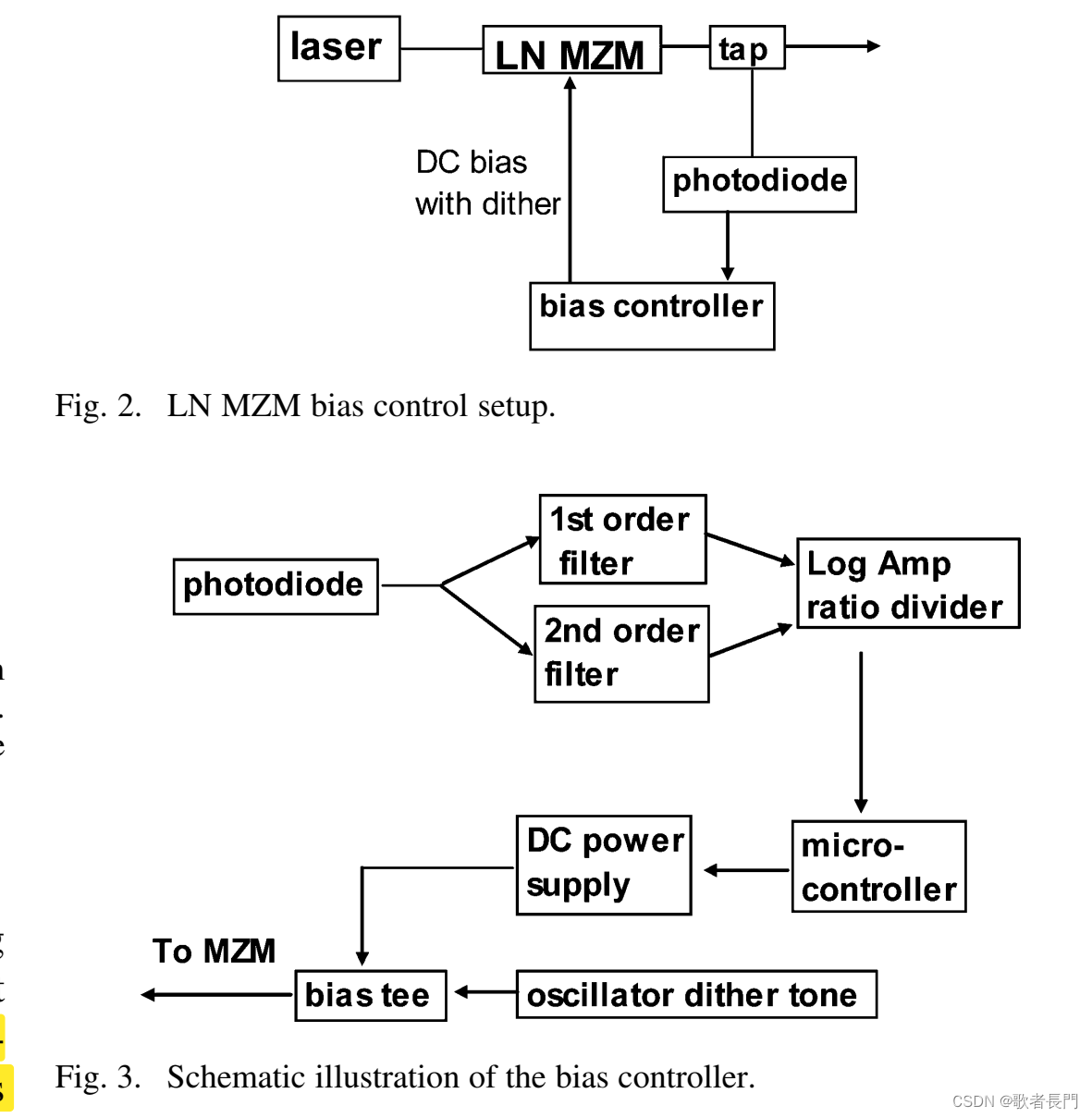
仿真和实验验证的曲线的对比：

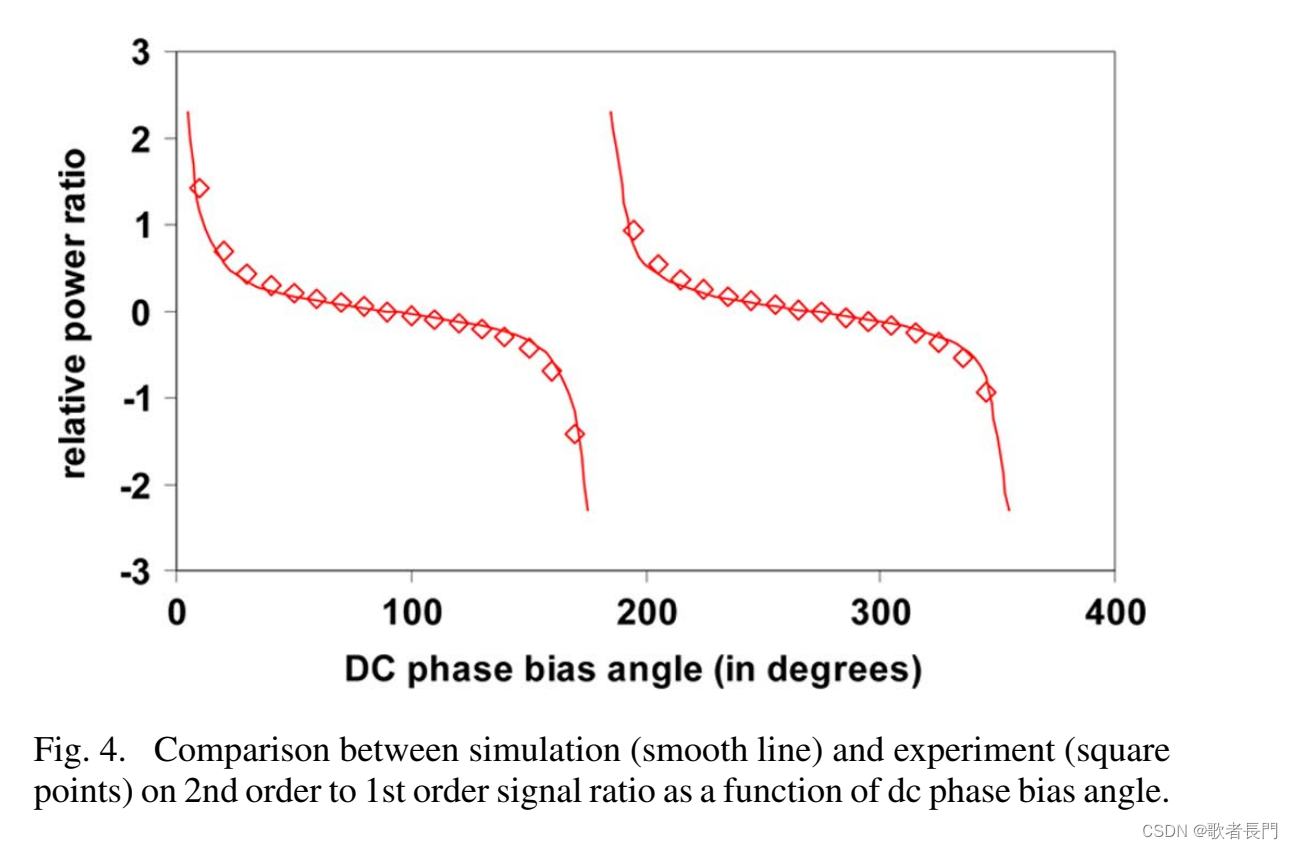
图5描述的是精确度和稳定性：

图6则展示了不同得抖动信号电压幅值对于偏置控制相位偏差的影响，并推测更低的电压引起的偏差更大的原因是硬件自身的噪声的影响淹没了抖动信号。

四、总结

本文展示了一种新颖而通用的偏置控制技术，与输入功率无关，不需要总是修正，且可以锁定在沿MZM传递函数曲线任何位置。