数据结构 二叉树篇之顺序存储结构

目录

前言

一、二叉树的存储结构

1.顺序存储

2.链式存储

二、顺序存储-堆的概念及结构

1.堆的概念

2.堆的实现

2.1向上取整

?2.2向下取整

三、全部代码?

总结

---

前言

????????我们上章讲到了树的基本结构，也提到了二叉树的基本概念，这章我们就要讲讲二叉树的存储结构了，二叉树有两种存储结构，顺序存储和链式存储，本章主要是讲解顺序存储该如何理解和创建。

---

一、二叉树的存储结构

二叉树的存储结构有两种，顺序存储、链式存储。

1.顺序存储

????????循序存储是使用数组来存储的，一般数组只适合表示完全二叉树，因为不是完全二叉树是会造成空间的浪费，而一般使用堆才会用数组存储，二叉树的顺序存储在物理上是一个数组，而在逻辑上还是一个二叉树的结构。堆在本章我也会跟大家解释一下他是一种什么原理和概念的。

完全二叉树：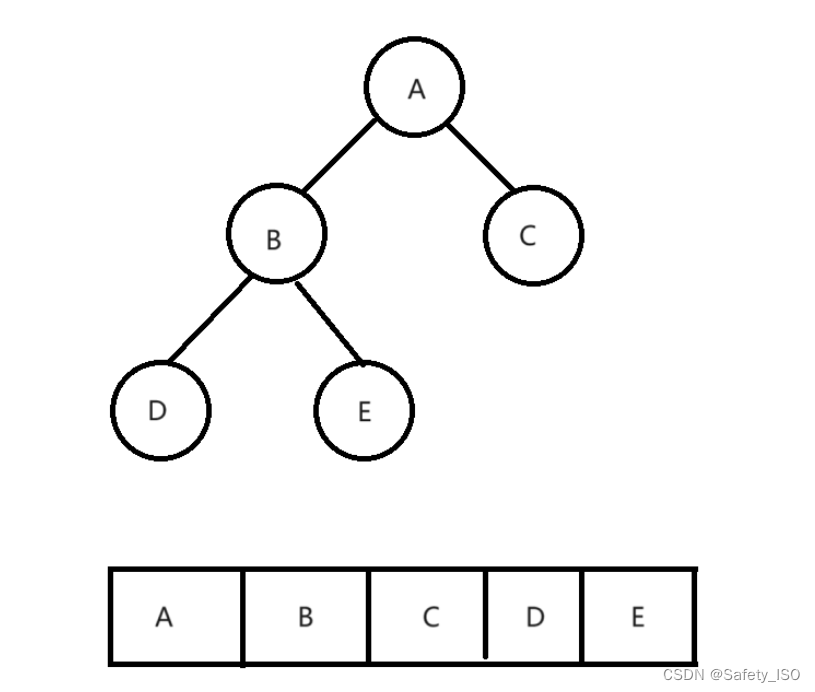

非完全二叉树：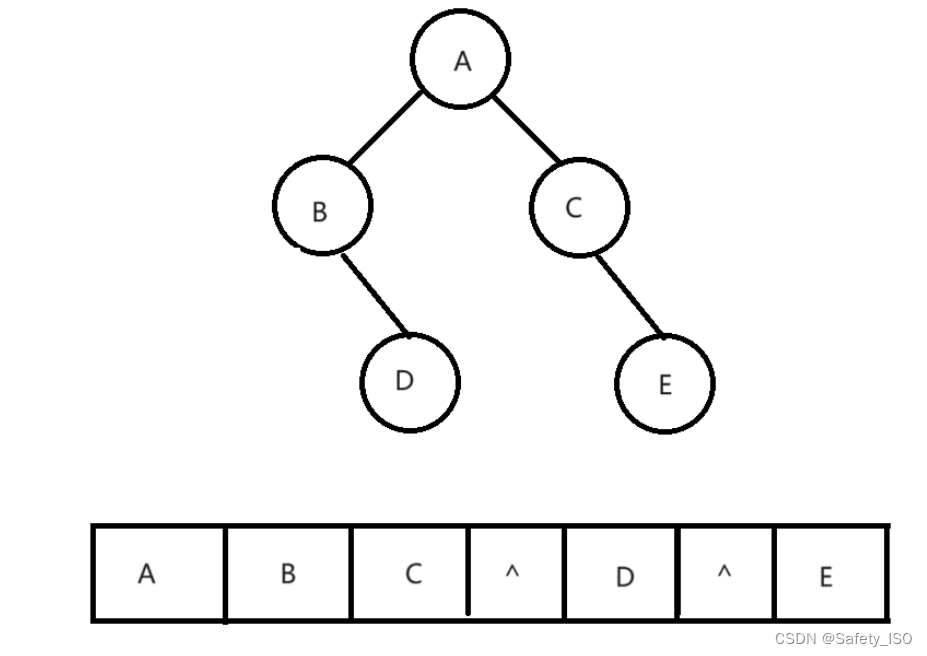

^代表空
从以上图可看出完全二叉树可以在数组中占满空间的，而非完全二叉树并不会占满所有空间。

2.链式存储

用链表表示一棵二叉树，通常由两种方法表示：

1.左右孩子法/二叉链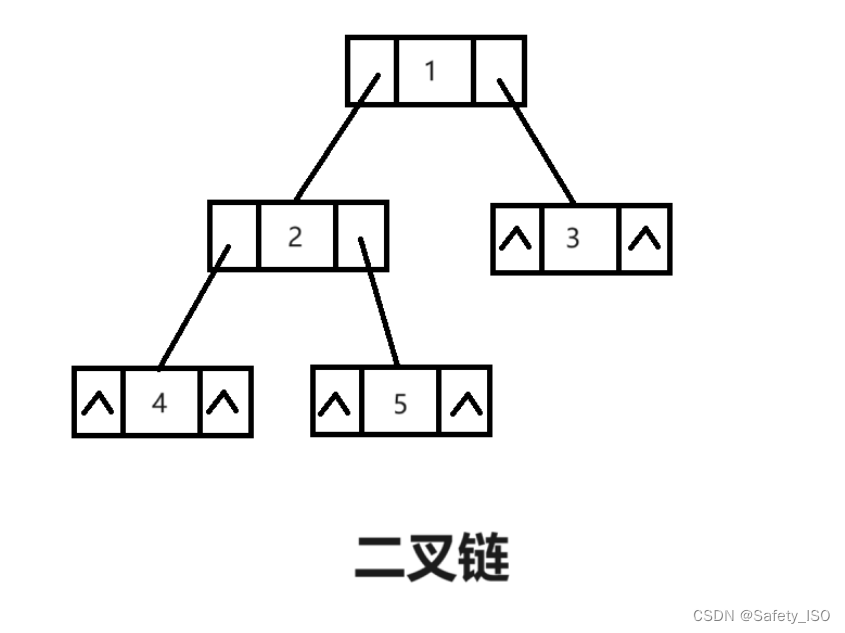

结构定义：

typedef int BTDataType;
struct BTreeNode{
    struct BTreeNode* pleft;
    struct BTreeNode* pright;
    BTDataType date;
}

?2.三叉链表

结构定义：

typedef int BTDataType;
struct BTreeNode{
    struct BTreeNode* pleft;
    struct BTreeNode* pright;
    struct BTreeNode* parent;
    BTDataType date;
}

二、顺序存储-堆的概念及结构

1.堆的概念

????????堆就是以二叉树的顺序存储方式来存储元素，同时又要满足父亲结点存储数据都要大于儿子结点存储数据的一种数据结构。堆有两种结构大堆和小堆，大堆就是父亲结点数据大于儿子结点数据，小堆则反之。

小堆：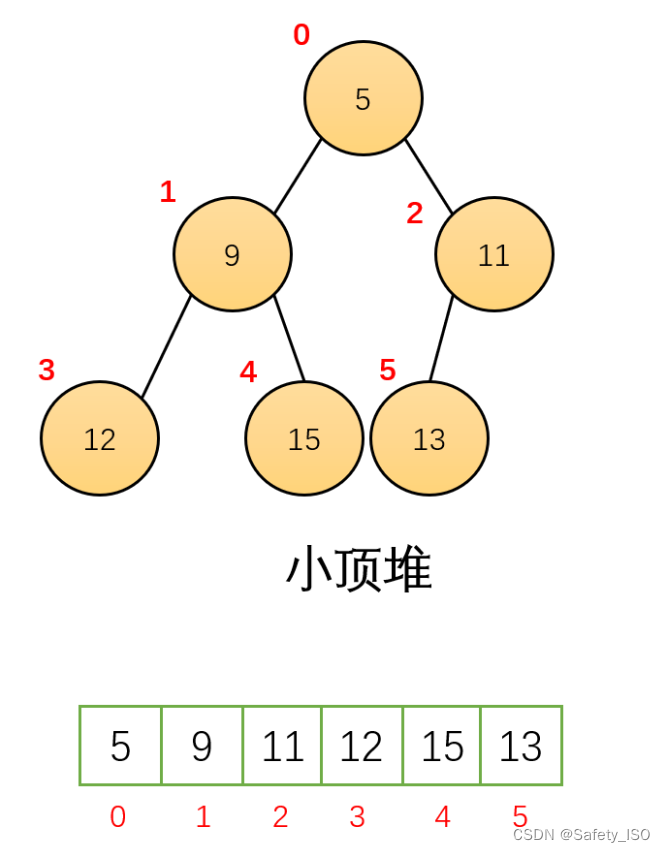

大堆：

2.堆的实现

? ? ? ? 通过上面的讲解我们知道堆就是一个数组，那我们对堆的结构创建就非常简单了，就跟之前创建一个顺序表是一样的：

typedef int HPDataType;
typedef struct Heap {
	HPDataType* a;
	int size;
	int capacity;
}hp;

那么我们当拿到一组乱序的数据数组，我们该如何将数组调整为堆呢？这里我们就要学一个向上取整和向下取整了，假设我们已经有一组数据为：

int a[] = { 2,46,7,4,3,7,9,40,0 };

?我们该如何调整呢？首先我们先把这数组抽象成一个二叉树，我们再从抽象树中逐个逐个调整。

可以看出，以上的顺序完全不符合堆中任何一种规律，那我们就把数组调整为小堆吧，后面的思路都是用小堆去实现，我们先说向上取整。

2.1向上取整

????????向上取整的思路是假设我们需要将数组最后一个数往上移动，去寻找他合适的位置，我们搭建小堆的话，最后一个位置的 0 需要跟他的父节点去做比较，当孩子节点比父节点小时需要互换位置，上一章我也提到了当得知孩子节点该如何找到父节点呢？直接（child - 1）/ 2 即可算出父节点的位置了，那么我们也可以发现 0 跟 4比较时是比 4 小的所以将准备交换节点。

? ? ?

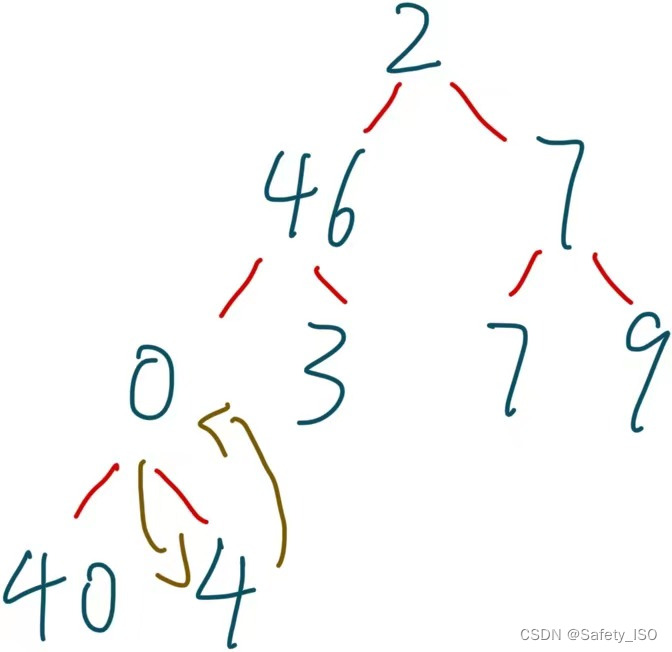
? ? ? ? 那么接下来继续重复以上的步骤，从孩子节点找到父节点的位置，继续比较，以达到适合0的位置。

? ? ??

????????当节点孩子小于 0 时代表已经成为根节点了，无需继续比较，还有当孩子节点是比父节点大时，不符合大堆的规则，就无需进行节点交换了，跳出循环即可，代码如下：

//向上取整
void AjoinUp(HPDataType* a, int child) {
	int parent = (child - 1) / 2;
	while (child>0) {
		if (a[parent] > a[child]) {
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}

?2.2向下取整

????????ok ok我们现在准备来到向下取整的环节，现在我们需要思考一个问题，假设一个堆中已经是大小堆中的其中一个，我们还是继续用小堆吧，在小堆里假设我们需要删除尾元素，很简单是吧，直接删就完事，我们看看图简单理解些：

? ??? ?

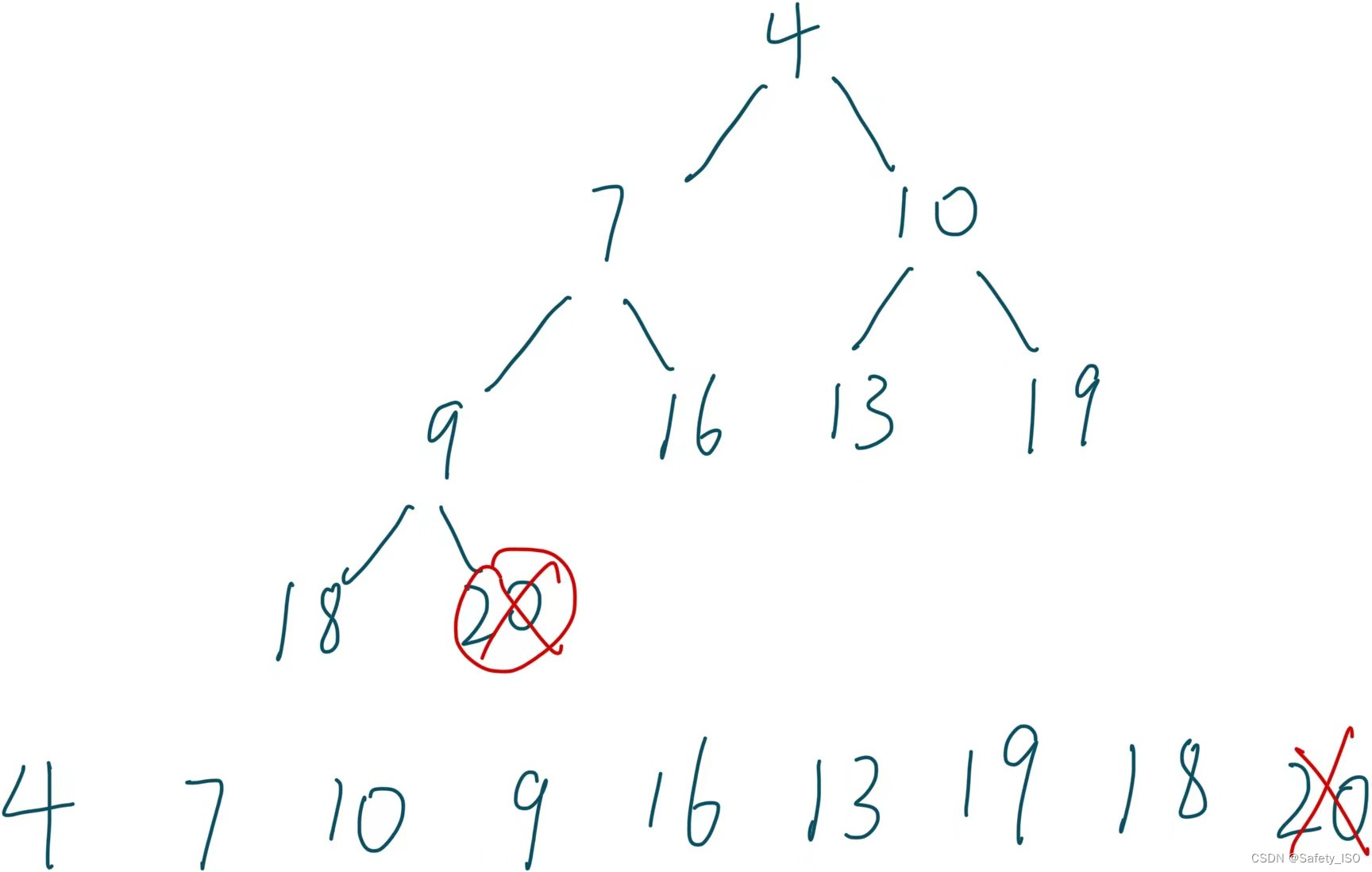
? ? ? ? 那么我们该如何头删呢？好，头删容易啊，直接把第一个元素除外后面的元素往前挪动一位不就可以了吗？真的是如此吗，好我们试一下，继续上图：

我们假设先用这个小堆数组：

进行头删元素：

头删之后从数组上抽象成树看看：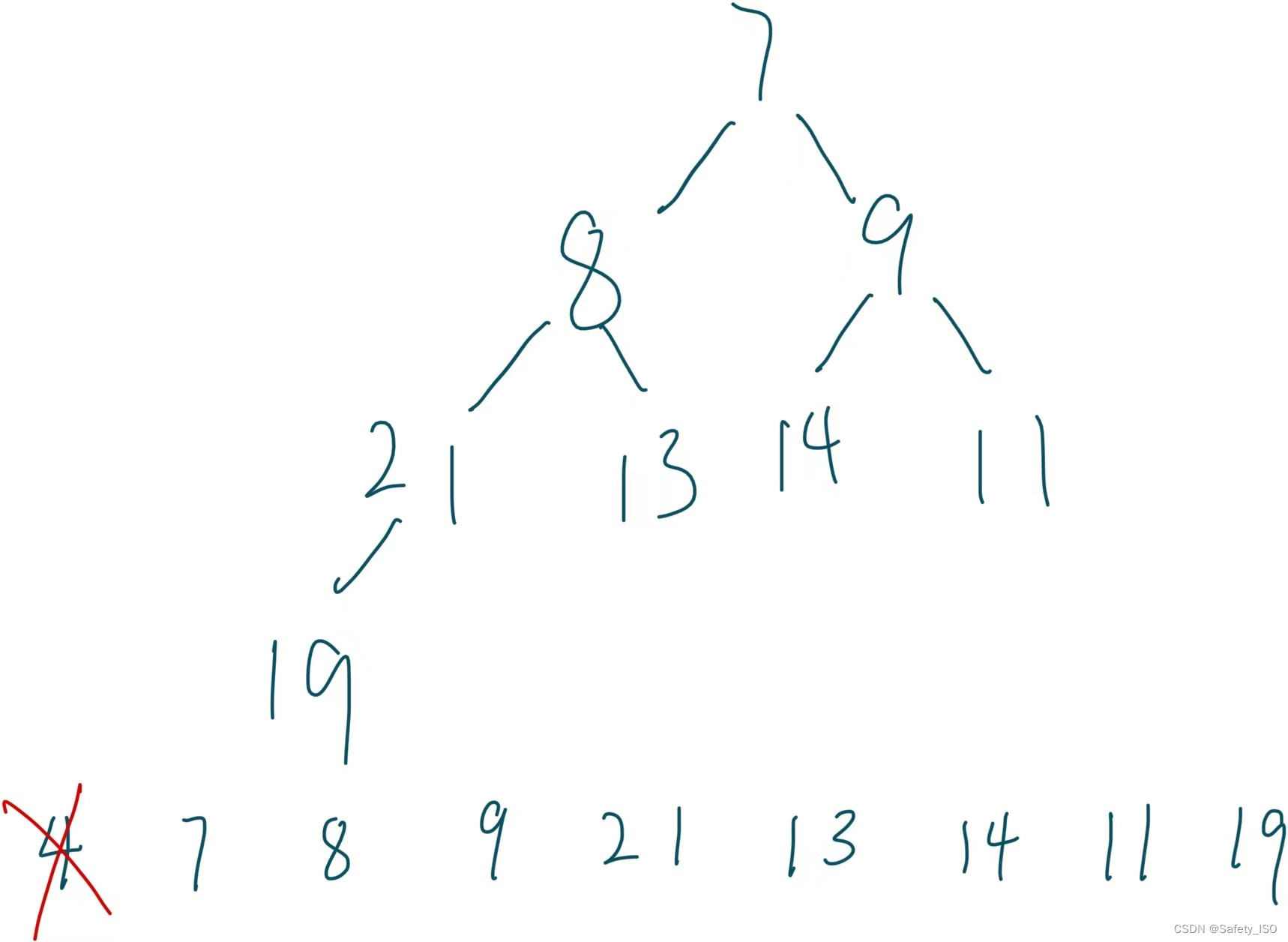

好，此时就发现一个问题了，这是小堆吗？这还是小堆吗？明显不是，我们可以看看树中 21 - 19中已经不符合小堆的规则了，所以我们直接进行头删是不对的，那我们接下来就需要学一个向下取整了，那我们需要怎么操作呢？

? ? ? ? 从上一个案例我们已经得知直接删除是不可行的，所以我们该如何头删进行向下取整，首先我们需要将头元素和尾元素进行交换，再继续向下取整操作即可，然后再将数组有效范围减一就行啦，那么向下取整该如何判断呢？大致原理是和向上取整差不多的，我们还是以画图表达出来：

我们初始已经排号的小堆：

首先首尾交换元素：

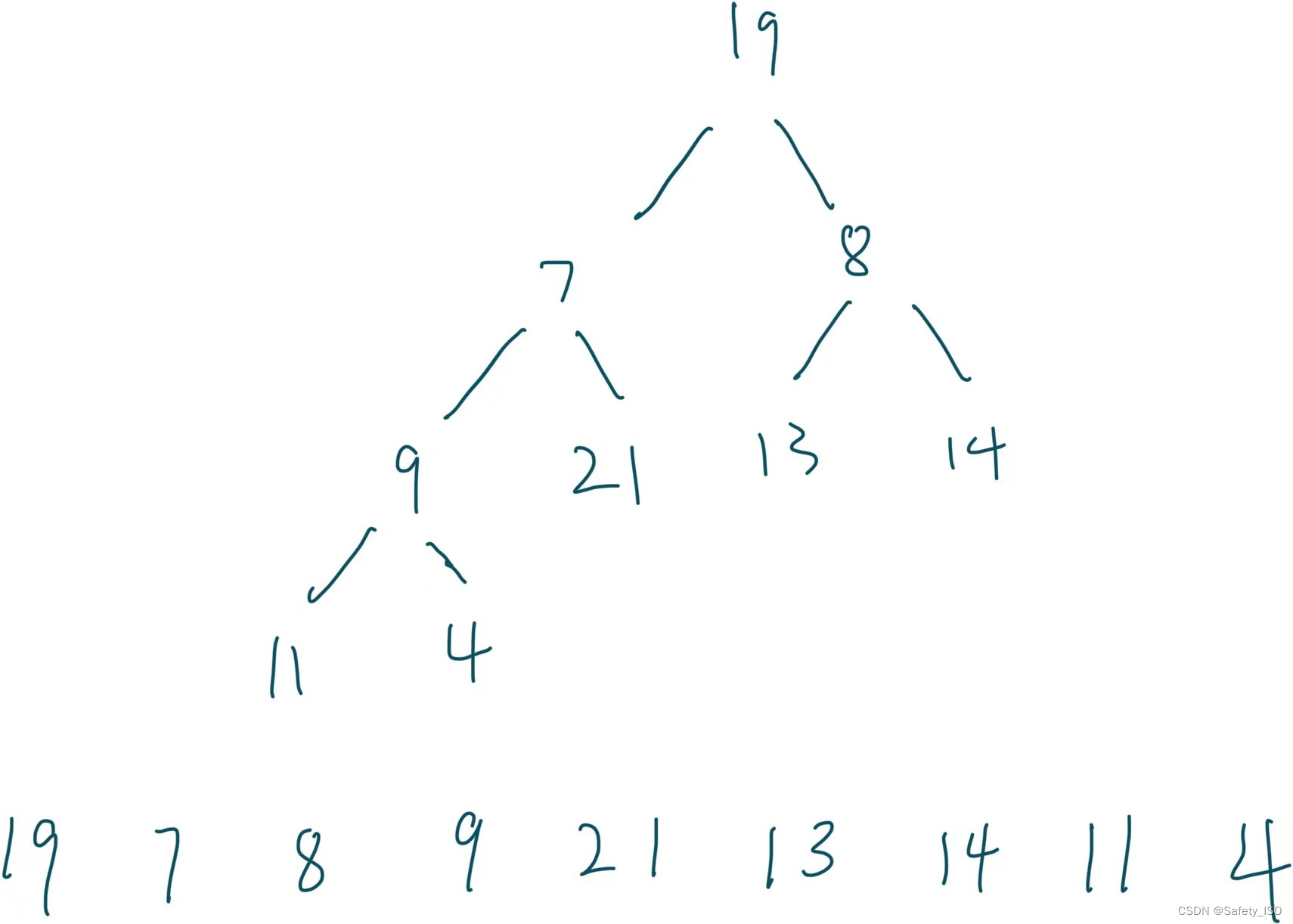
交换成功后进行首元素的向下取整，比较孩子节点里的最小元素对比，我们得知父节点该如何求出孩子节点呢？这在上一章的二叉树的基本概念提到了，我们得知父节点求孩子节点直接 （parent * 2）+ 1 （左孩子）或?+ 2 （右孩子）即可求出，这时候我们需要判断哪个孩子节点的元素是最小的，从而进行夫儿节点的交换。

? ? ??? ? ? ??

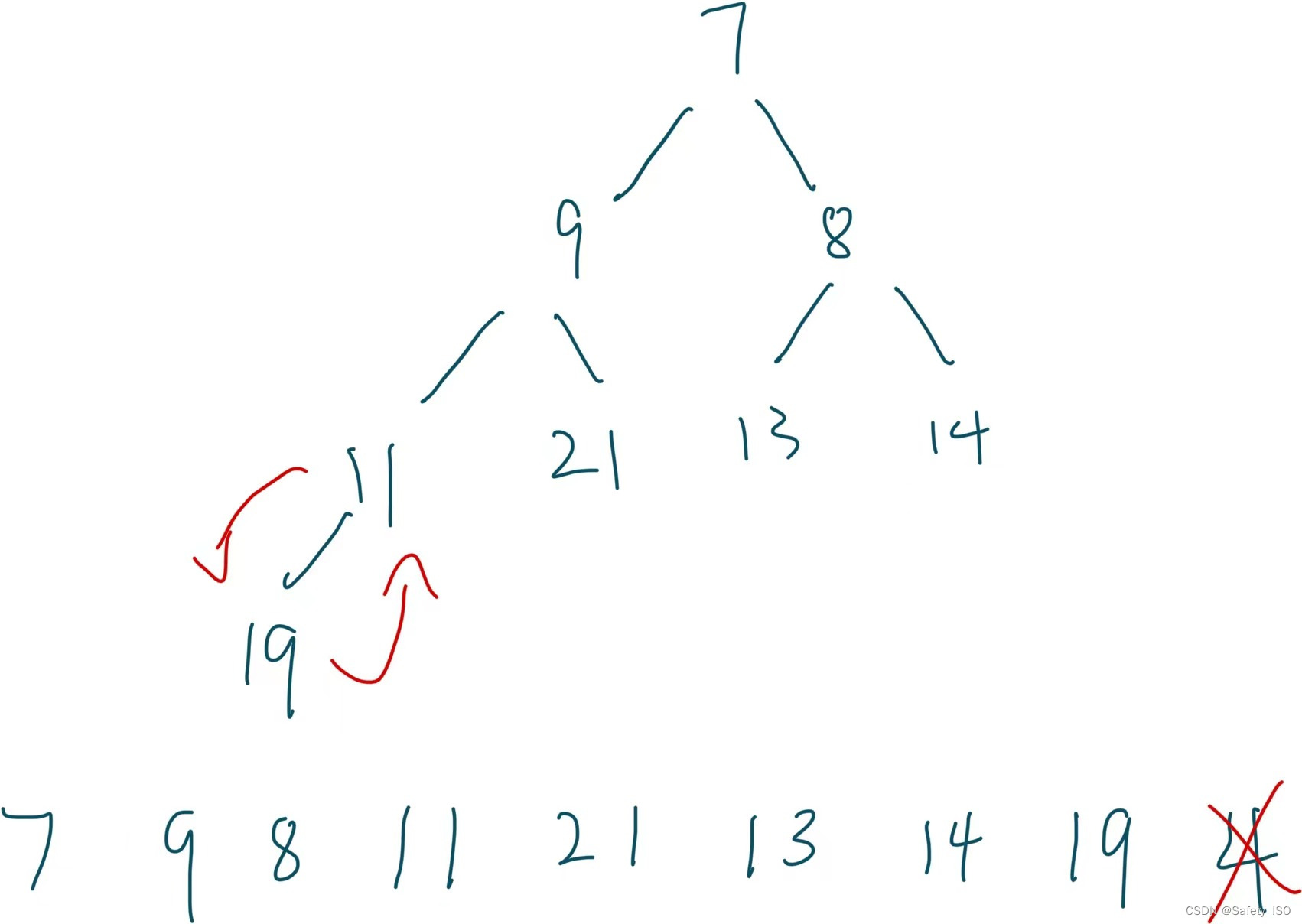
经过几次的交换我们就真正得到了个小堆数组元素。

具体代码操作：

void AjoinDown(HPDatatpye* arr, int size, int parent) {
	int child = parent * 2 + 1;
	while (child < size) {
		if (child + 1 < size && arr[child] < arr[child + 1]) {
			child = child + 1;
		}
		if (arr[parent] < arr[child]) {
			Swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

三、全部代码?

Heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>


typedef int HPDataType;
typedef struct Heap {
	HPDataType* a;
	int size;
	int capacity;
}hp;

//堆初始化
void HeapInit(hp* php);
//堆销毁
void HeapDestory(hp* php);
//堆插入
void HeapPush(hp* php, HPDataType x);
//堆删除
void HeapPop(hp* php);
// 取堆顶的数据
HPDataType HeapTop(hp* php);
// 堆的数据个数
int HeapSize(hp* php);
// 堆的判空
bool HeapEmpty(hp* php);

Heap.c

#define  _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"

//堆初始化
void HeapInit(hp* php){
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}
//堆销毁
void HeapDestory(hp* php) {
	assert(php);
	if (php->a) {
		free(php->a);
		php->size = 0;
		php->capacity = 0;
	}
}

void Swap(HPDataType* p, HPDataType* q) {
	HPDataType emp = *p;
	*p = *q;
	*q = emp;
}

//向上取整
void AjoinUp(HPDataType* a, int child) {
	int parent = (child - 1) / 2;
	while (child>0) {
		if (a[parent] > a[child]) {
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}

//堆插入
void HeapPush(hp* php, HPDataType x) {
	assert(php);
	if (php->size == php->capacity) {
		int newcapa = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* p = (HPDataType*)realloc(php->a, newcapa * sizeof(HPDataType));
		if (p == NULL) {
			perror("realloc p");
			exit(-1);
		}
		php->a = p;
		php->capacity = newcapa;
	}
	php->a[php->size] = x;
	php->size++;
	AjoinUp(php->a, php->size - 1);
}

//向下取整
void AjoinDown(HPDataType* a,int size ,int parent){
	int child = parent * 2 + 1;
	while (child < size) {
		if (child + 1 < size && a[child] > a[child + 1]) {
			child = child + 1;
		}
		if (a[parent] > a[child]) {
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

//堆删除
void HeapPop(hp* php) { 
	assert(php);
	Swap(&(php->a[0]), &(php->a[php->size - 1]));
	AjoinDown(php->a,php->size -1 , 0);
	php->size--;
}

// 取堆顶的数据
HPDataType HeapTop(hp* php) {
	return php->a[0];
}
// 堆的数据个数
int HeapSize(hp* php) {
	return php->size;
}
// 堆的判空
bool HeapEmpty(hp* php) {
	return php->size == 0;
}

?test.c

#define  _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

int main() {
	int a[] = { 2,46,7,4,3,7,9,0,40 };
	hp phead;
	HeapInit(&phead);
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++) {
		HeapPush(&phead, a[i]);
	}
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++) {
		printf("%d ", phead.a[i]);
	}
	printf("\n");
	//int k = 3;
	//while (k--) {
	//	HeapPop(&phead);
	//}
	
	while (!HeapEmpty(&phead)) {
		printf("%d ", HeapTop(&phead));
		HeapPop(&phead);
	}

	HeapDestory(&phead);
}

?

---

总结

? ? ? ? 该二叉树的堆是以创建了一个数组的形式创建的，下一章我们会探讨一下，如何在不创建一个结构体的情况下，直接在原数组的情况下进行大小堆调整，并且在大小堆的基础上我们聊聊如何在堆上进行排序，希望大家能学会喔！！！