动态规划：01背包问题(一)

本题力扣上没有，是刷的卡码网第46题感兴趣的小伙伴可以去刷一下，是ACM模式。本篇讲解二维dp数组来解决01背包问题，下篇博客将用一维dp数组来解决01背包问题。

题目：

46. 携带研究材料

时间限制：5.000S 空间限制：128MB

题目描述:

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的空间，并且具有不同的价值。
小明的行李空间为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料只能选择一次，并且只有选与不选两种选择，不能进行切割。

输入描述:

第一行包含两个正整数，第一个整数 M 代表研究材料的种类，第二个正整数 N，代表小明的行李空间。

第二行包含 M 个正整数，代表每种研究材料的所占空间。

第三行包含 M 个正整数，代表每种研究材料的价值。

输出描述:

输出一个整数，代表小明能够携带的研究材料的最大价值。

输入示例:

6 1
2 2 3 1 5 2
2 3 1 5 4 3

输出示例:

5

提示信息:

小明能够携带 6 种研究材料，但是行李空间只有 1，而占用空间为 1 的研究材料价值为 5，所以最终答案输出 5。

数据范围：
1 <= N <= 1000
1 <= M <= 1000
研究材料占用空间和价值都小于等于 1000

思路：

01 背包：

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二维dp数组01背包：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

依然动规五部曲分析。

1. 确定dp数组以及下标的含义

对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

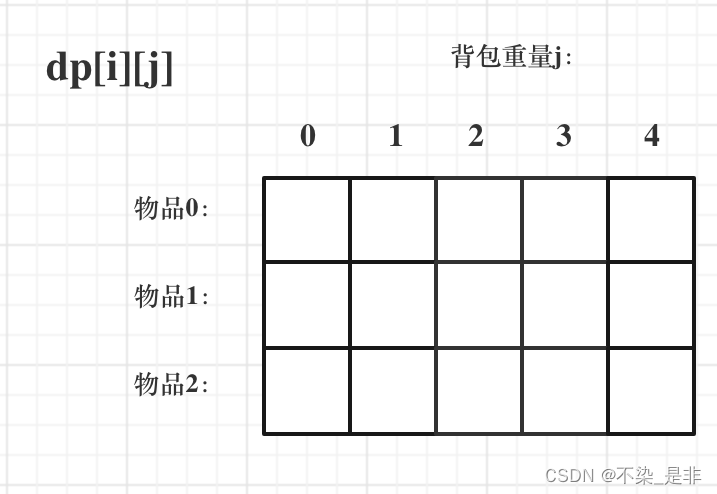
要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。

2. 确定递推公式

再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

3. dp数组如何初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

如图：

在看其他情况。

状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

代码初始化如下：

    # 创建二维数组dp，用于保存状态转移的结果
    dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
#   for i in range(bag_nums):  此处已把所有dp数组初始为0了 故此步可省略
#       dp[i][0] = 0
    # 初始化第一个背包的状态
    for j in range(weight[0], bag_weight + 1):
        dp[0][j] = value[0]

此时dp数组初始化情况如图所示：

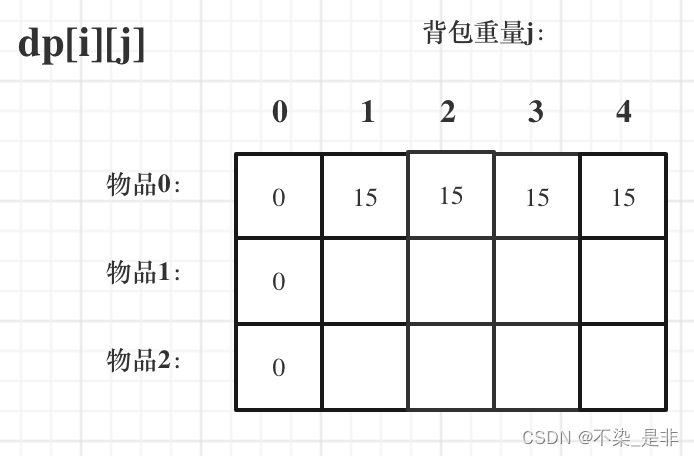
dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？

其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖。

初始-1，初始-2，初始100，都可以！

但只不过一开始就统一把dp数组统一初始为0，更方便一些。

最后初始化代码如下：

def result():
    # 读取输入的数据
    N = [int(x) for x in input().split()]  # 读取背包数量和背包总重量
    weight = [int(x) for x in input().split()]  # 读取每个物品的重量
    value = [int(x) for x in input().split()]  # 读取每个物品的价值
    bag_nums = N[0]  # 背包数量
    bag_weight = N[1]  # 背包总重量
    # 创建二维数组dp，用于保存状态转移的结果
    dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
    # 初始化第一个背包的状态
    for j in range(weight[0], bag_weight + 1):
        dp[0][j] = value[0]

到了这里应该有很多人还是不太明白代码为什么这么写，为什么j要从weight[0]开始遍历到bag_weight 结束（这里的代码是直接看着题目描述的输出和输入案例来AC的），我刚开始也不太理解，后来发现还是自己没审好dp数组的初始化步骤和过程，dp数组首先对第一列开始全部初始化为0（我在定义dp数组的时候就已经全部初始化为0了，所以此步骤可以省略）

之后把第一行初始化，这里初始化并不需要排序啊什么的，就取weight数组的第一个元素，看它是否满足小于背包（bag_weight）的重量，如果小于则把该weight数组第一个元素对应重量下的value(价值)赋给dp[0][j]，从dp[0][j]到dp[0][bag_weight]全部都赋值为value[0]

4. 确定遍历顺序

在上述图片中可以看出，有两个遍历的维度（两层for循环）：物品与背包重量

那么问题来了，先遍历 物品还是先遍历背包重量呢？

其实都可以！！ 但是先遍历物品更好理解。

5. 举例推导dp数组

来看一下对应的dp数组的数值，如图：

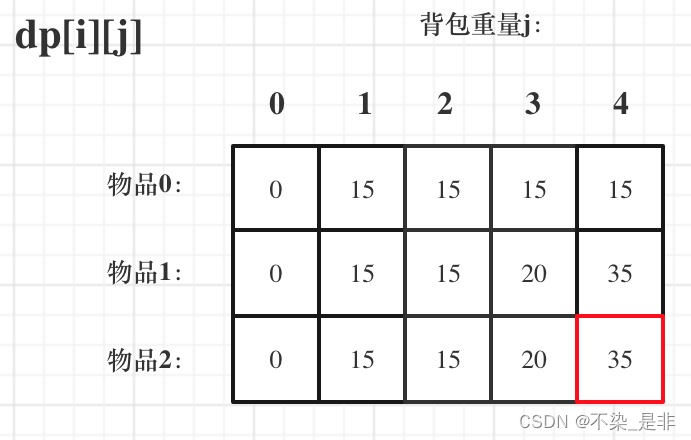
这里其实就是确认最后的返回值是什么，因为dp数组的含义是最大的价值（不管重量如何变化，取的都是最大的价值总和），所以应该返回dp数组的最后一个元素

return dp[bag_nums - 1][bag_weight]  # 返回最后一个背包的最大价值

代码及详细注释：

def result():
    # 读取输入的数据
    N = [int(x) for x in input().split()]  # 读取背包数量和背包总重量
    weight = [int(x) for x in input().split()]  # 读取每个物品的重量
    value = [int(x) for x in input().split()]  # 读取每个物品的价值
    bag_nums = N[0]  # 背包数量
    bag_weight = N[1]  # 背包总重量
    # 创建二维数组dp，用于保存状态转移的结果
    dp = [[0] * (bag_weight + 1) for _ in range(bag_nums)]
    # 初始化第一个背包的状态
    for j in range(weight[0], bag_weight + 1):
        dp[0][j] = value[0]
    # 状态转移，计算每个背包的最大价值
    for i in range(1, bag_nums):
        for j in range(1, bag_weight + 1):
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]  # 当前背包的重量大于背包总重量，不放入当前物品
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])  # 放入当前物品或者不放入当前物品，取最大值
    return dp[bag_nums - 1][bag_weight]  # 返回最后一个背包的最大价值

if __name__ == '__main__':
    print(result())  # 输出结果