斐波那契的平方、立方问题——考虑几何立体意义(数形结合法):P9510
https://www.luogu.com.cn/problem/P9510
关于斐波那契和的平方,其实就是正方形的面积和:
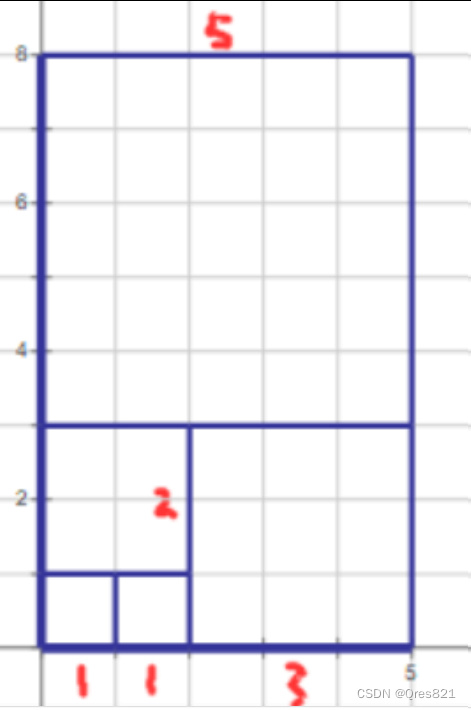
也就是 f ( i ) ? f ( i + 1 ) f(i)*f(i+1) f(i)?f(i+1)
我们现在要求立方,但我们可以可以发现红色部分的结果是一样的:
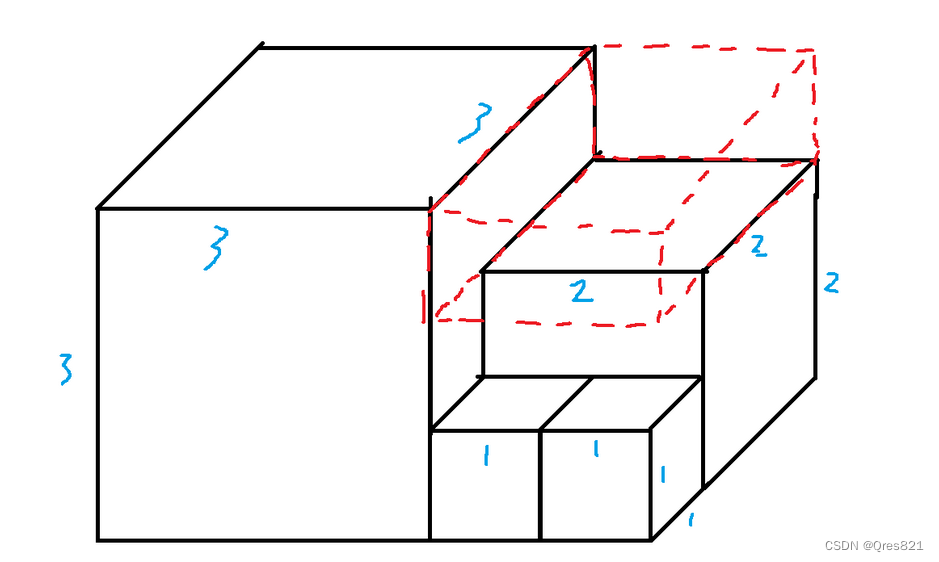
直接三条棱表示除了,就是 f ( i ) ? f ( i ? 1 ) ? f ( i ? 2 ) f(i)*f(i-1)*f(i-2) f(i)?f(i?1)?f(i?2)。因此我们可以全部约掉(在 立体图形相当于在所有空位全部补上了),所以刚好就是 : f ( i ) 2 ? f ( i + 1 ) f(i)^2*f(i+1) f(i)2?f(i+1)。我们加上外面的常数项直接矩阵快速幂即可。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于Python+Django,开发一款房屋租赁系统
- 系列二、Spring Cloud Alibaba简介
- iS-RPM2023.2.0.0新版本发布
- std::lock_guard 是 C++ 标准库中,用于简化互斥量的管理。它提供了一个异常安全的方式来锁定和自动解锁互斥量。
- D3DCompiler_47.dll下载-D3DCompiler_47.dll文件缺失的详细解决方案
- java中string转timestamp(日期类型转换)
- 《繁花》落尽,人生百态美丽却很短暂
- 图神经网络研究与应用:多方向发展与未来趋势
- Qt QComboBox组合框控件
- 解决 ssh: connect to host github.com port 22: Connection timed out