LOAM: Lidar Odometry and Mapping in Real-time 论文阅读
论文链接
LOAM: Lidar Odometry and Mapping in Real-time
0. Abstract
提出了一种使用二维激光雷达在6自由度运动中的距离测量进行即时测距和建图的方法
距离测量是在不同的时间接收到的,并且运动估计中的误差可能导致生成的点云的错误配准
- 本文的方法在不需要高精度测距或惯性测量的情况下同时实现了低漂移和低计算复杂性
- 关键思想是将同时定位和建图的复杂问题划分为两个算法
- 一个算法以高频率进行测距,但精度较低,用于估计激光雷达的速度
- 另一个算法以数量级较低的频率进行精准匹配和点云配准
?
1. Intro
- 使用激光雷达进行地图绘制很常见,因为激光雷达可以提供高频测量范围,在测量距离时误差相对恒定
- 激光雷达本身在不断运动,准确的建图需要了解连续激光测距过程中激光雷达的姿态
- 一种常见方法是使用独立的位置估计(例如通过GPS/惯性导航系统)将激光点云注册到固定坐标系中
- 另一种方法使用里程计测量,例如来自轮式编码器或视觉里程计系统来注册激光点云(因为里程计会随之时间对于小的运动量进行积分,存在漂移的问题)
本文工作考虑使用二轴激光雷达在六自由度中创建带有低漂移测距的地图。使用激光雷达的一个关键优势是它对环境光线和场景光纹的不敏感。本文的工作并不包括闭环
- 该方法实现了低漂移和低计算复杂度,无需高精度测距或惯性测量
- 两个算法都提取位于尖锐边缘和平面表面上的特征点,并将特征点分别匹配到边缘线段和平面表面补丁
- 在测程算法中,通过确保快速计算来找到特征点的对应关系
- 在建图算法中,通过检查局部点簇的几何分布,通过相关的特征值和特征向量来确定对应关系
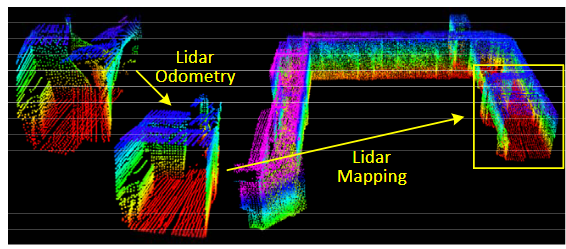
Fig. 1 该方法旨在使用移动的二轴激光雷达进行运动估计和映射。由于激光点是在不同的时间接收到的,因此由于激光雷达的运动而在点云中存在畸变(显示在左侧的激光云中)。我们提出的方法通过两个并行运行的算法分解问题。一个里程计算法估计激光雷达的速度并校正点云中的畸变,然后一个映射算法将点云匹配和注册以创建地图。两个算法的结合确保了问题在实时中得到解决的可行性。
2. Related Work
- 当激光雷达扫描速率远高于其外部运动时,扫描中的运动扭曲经常可以忽略。可以使用标准的ICP方法来匹配不同扫描之间的激光回波
- 有的工作提出了一种两步方法来消除失真:首先是基于ICP的速度估计步骤,然后是使用计算出的速度进行失真补偿步骤
然而,如果扫描运动相对缓慢,运动失真可能很严重。当使用2轴激光雷达时,一轴通常比另一轴慢得多。通常,还使用其他传感器来提供速度测量,借此可以消除失真
如果使用2轴激光雷达而不受其他传感器的辅助,运动估计和畸变校正会成为一个问题
- 从激光强度返回中创建视觉图像,并匹配图像之间的视觉上不同特征以恢复地面车辆的运动
本文的方法在里程计算法中使用类似的线性运动模型,但使用不同类型的特征。本文的方法在笛卡尔空间提取和匹配几何特征,并对点云密度要求较低
3. Notation and Task Descrption
本文研究的问题是使用3D激光雷达感知的点云执行自我运动估计,并构建所经过环境的地图。我们假设激光雷达已经进行了预校准。我们还假设激光雷达的角速度和线速度在时间上是平滑连续的,没有突变。
我们使用右上标来指示坐标系。我们将扫描完成一次覆盖定义为扫描。我们使用右下标 k , k ∈ Z + k, k ∈ Z^+ k,k∈Z+ 来表示扫描,并使用 P k \mathcal{P}_k Pk? 来表示第 k k k 次扫描期间感知到的点云。定义两个坐标系
-
激光雷达坐标系 { L } \{L\} {L} 是一个三维坐标系,其原点位于激光雷达的几何中心。X 轴指向左侧,Y 轴指向上方,Z 轴指向前方。点 i , ( i ∈ P k ) i,(i ∈ \mathcal{P}_k) i,(i∈Pk?)在 { L k } \{L_k\} {Lk?} 中的坐标表示为 X ( k , i ) L X^L_{(k,i)} X(k,i)L?。
-
世界坐标系 { W } \{W\} {W} 是一个与初始位置上的 { L } \{L\} {L} 重合的三维坐标系。 { W k } \{W_k\} {Wk?} 中点 i , ( i ∈ P k ) i,(i ∈ \mathcal{P}_k) i,(i∈Pk?) 的坐标是 X ( k , i ) W X^W_{(k,i)} X(k,i)W?。
问题描述:给定一系列 LiDAR 点云 P k \mathcal{P}_k Pk?,其中 k ∈ Z + k ∈ Z^+ k∈Z+,计算每次扫描 k k k 期间的 LiDAR 自我运动,并利用构建经 P k \mathcal{P}_k Pk? 过的环境的地图
4. System Overview
A. 激光雷达硬件
-
本文的研究是基于一个自定义的3D Hokuyo UTM-30LX激光扫描仪进行验证,但不限于该设备
-
该激光扫描仪的视野为180度,分辨率为0.25度,扫描速率为40行/秒
-
激光扫描仪连接到一个电机,电机以每秒180度的角速度在水平方向上旋转,旋转角度范围为-90度到90度,将激光扫描仪的水平方向作为零度
-
对于连续旋转的激光雷达,一个扫描只是半球形的旋转
-
一个内置的编码器以0.25度的分辨率测量电机的旋转角度,利用这个角度,将激光点投影到激光雷达坐标系 { L } \{L\} {L} 中

Fig. 2 本研究使用的3D激光雷达由一个由电机驱动的Hokuyo激光扫描仪和一个测量旋转角度的编码器组成。激光扫描仪的视场角为180?,分辨率为0.25?。扫描频率为40行/秒。电机的控制范围为从-90?到90?,以激光扫描仪的水平方向为零。
-
B. 软件系统概述
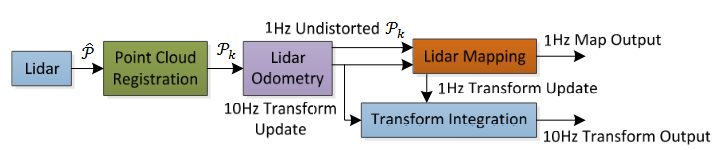
Fig. 3 激光雷达轮式里程计及地图制图软件系统的框图。
上图显示了软件系统的示意图。设 P ^ \hat{\mathcal{P}} P^ 为激光扫描中接收到的点。在每次扫描中, P ^ \hat{\mathcal{P}} P^ 被注册在 { L } \{L\} {L} 中。扫描k期间的组合点云形成 P k \mathcal{P}_k Pk? 。然后, P k \mathcal{P}_k Pk? 经过两个算法处理。激光雷达测距法基于点云计算两次连续扫描之间的激光雷达运动。估计的运动被用来校正 P k \mathcal{P}_k Pk? 中的失真。该算法以约10Hz的频率运行。输出进一步由激光雷达地图匹配和注册进行处理,该过程以1Hz的频率将无失真的点云对齐到地图上。最后,由这两个算法发布的姿态变换被融合生成约10Hz的转换输出,涉及激光雷达在地图上的姿态。
5. 激光雷达里程计
A. 特征点提取
- 激光雷达自然地生成了一组不均匀分布的点 P k \mathcal{P}_k Pk? 。激光扫描仪的返回分辨率在扫描内为0.25度,这些点位于一个扫描平面上。
- 由于激光扫描仪以180度/秒的角速度旋转并以40Hz生成扫描,垂直于扫描平面的方向上的分辨率为180度/40 = 4.5度
特征点是根据个别扫描的信息从 P k \mathcal{P}_k Pk? 中提取出来的,具有共面几何关系
-
选择位于锐边和平面表面区域上的特征点
-
设 i i i 为 P k \mathcal{P}_k Pk? 中的一个点, i ∈ P k i∈\mathcal{P}_k i∈Pk? ,设S为激光扫描仪在同一次扫描中返回的i的连续点集
-
由于激光扫描仪按顺时针或逆时针顺序生成点返回, S \mathcal{S} S 包含其点的一半位于i的两侧,并且两个点之间的间隔为0.25°
-
定义一个术语来评估局部表面的平滑度
c = 1 ∣ S ∣ ? ∣ ∣ X ( k , i ) L ∣ ∣ ∣ ∣ ∑ j ∈ S , ? j ≠ i ( X ( k , i ) L ? X ( k , j ) L ) ∣ ∣ . (1) c= \frac{1}{|\mathcal{S}|·||X^L_{(k,i)}||} ||\mathop{\sum}\limits_{j∈\mathcal{S},\ j\neq i}(X^L_{(k,i)}?X^L_{(k,j)})||. \tag{1} c=∣S∣?∣∣X(k,i)L?∣∣1?∣∣j∈S,?j=i∑?(X(k,i)L??X(k,j)L?)∣∣.(1) -
扫描中的点根据 c c c 值进行排序,然后选择具有最大 c c c 值的特征点,即边缘点,以及具有最小 c c c 值的特征点,即平面点
-
将扫描分为四个相同的子区域。每个子区域最多可以提供2个边缘点和4个平面点。只有当点 i i i 的 c c c 值大于或小于阈值,并且选择的点的数量不超过最大值时,才能将点i选择为边缘点或平面点
-
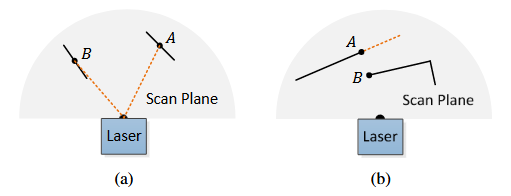
Fig. 4 (a) 实线段代表局部表面块。点A在与激光束(虚线橙色线段)成角度的表面块上。点B在与激光束大致平行的表面块上。我们将B视为不可靠的激光返回点,不选择其作为特征点。(b) 实线段是激光可观测的物体。点A在被遮挡区域的边界上(虚线橙色线段),可以被检测为边缘点。然而,如果从不同角度观察,则遮挡区域可以变化并变得可观测。我们不将A视为显著的边缘点或选择其作为特征点。
- 在选择特征点时,我们要避免选择其周围已选择的点,或者在局部平面表面(如图 4(a) 中的 B 点)上的点,这些点通常被认为是不可靠的。同时,我们也要避免选择位于遮挡区域边界上的点.如图 4(b) 所示的例子中,点 A 是激光云中的边缘点,因为它连接的表面(虚线段)被其他物体挡住了
- 为了避免选择前述的点,我们再次找出点集 S \mathcal{S} S。只有当 S \mathcal{S} S 不能形成与激光束大致平行的表面补丁,并且 S \mathcal{S} S 中没有点在激光束方向上与点 i i i 之间有断开,且同时离激光雷达比点 i i i 更近(例如图 4(b) 中的点 B),点 i i i 才能被选择
- 特征点是从最大
c
c
c 值开始选择作为边缘点,从最小
c
c
c 值开始选择作为平面点,如果选择了一个点
- 所选的边缘点或平面点的数量不能超过子区域的最大值
- 其周围的任何一个点都尚未被选择
- 不能位于近似平行于激光束的表面区域,也不能位于遮挡区域的边界上
B. 寻找特征点对应
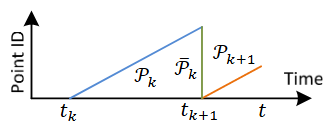
Fig. 6 重投影点云到扫描结束处。蓝色的线段表示在扫描k期间感知到的点云 P k \mathcal{P}_k Pk? 。在扫描 k k k 结束时, P k \mathcal{P}_k Pk? 被重新投影到时间戳 t k + 1 t_{k+1} tk+1? ,得到 P ˉ k \bar{\mathcal{P}}_k Pˉk?(绿色的线段)。然后,在第 k + 1 k + 1 k+1 次扫描中,将 P ˉ k \bar{\mathcal{P}}_k Pˉk? 和新感知到的点云 P k + 1 \mathcal{P}_{k+1} Pk+1?(橙色线段)一起用于估计激光雷达的运动。
激光雷达运动的测距算法估计在一次扫描中的运动。设 t k t_k tk? 为第 k k k 次扫描的起始时间
- 在每次扫描结束时,扫描中感知到的点云 P k \mathcal{P}_k Pk? 被重新投影到时间戳 t k + 1 t_{k+1} tk+1? 上(图 6 所示)
- 我们将重新投影的点云表示为 P ˉ k \bar{\mathcal{P}}_k Pˉk? 。在下一次扫描中, P ˉ k \bar{\mathcal{P}}_k Pˉk? 与新收到的点云 P k + 1 \mathcal{P}_{k+1} Pk+1? 一起被用来估计激光雷达的运动
从激光雷达点云中找到边缘点和平面点。假设 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1?和 H k + 1 \mathcal{H}_{k+1} Hk+1?分别为边缘点和平面点的集合。将 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中找到边线作为 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 中点的对应关系,并将平面块作为 H k + 1 \mathcal{H}_{k+1} Hk+1? 中点的对应关系。
- 注意,在第 k + 1 k+1 k+1 次扫描的开始, P k + 1 \mathcal{P}_{k+1} Pk+1? 是一个空集,随着扫描过程中接收到更多的点,它会不断增长。
- 在每次迭代中,使用当前估计的变换将 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 和 H k + 1 \mathcal{H}_{k+1} Hk+1? 投影到扫描开始的位置
- 让 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1? 和 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? 成为重映射的点集。对于 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1? 和 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? 中的每个点,找到 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中最近的邻近点(这里 P ˉ k \bar{\mathcal{P}}_k Pˉk? 存储在一个三维KD树中以实现快速索引)
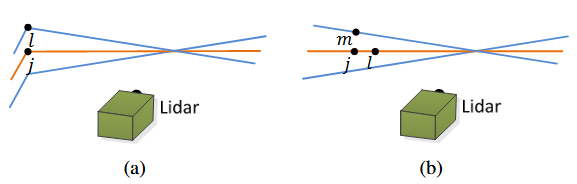
Fig. 7 在 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1? (a) 中,寻找边缘点的边缘线对应,并 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? (b) 中寻找平面点的平面片对应。在 (a) 和 (b) 中, j j j 是特征点 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中找到的最近点。橙色线代表与 j j j 相同的扫描,蓝色线代表两次连续的扫描。为了找到 (a) 中的边缘线对应,我们在蓝色线上找到另一个点 l l l,并表示为 ( j , l ) (j, l) (j,l) 。为了找到 (b) 中的平面片对应,我们在橙色和蓝色线上分别找到另外两个点 l l l 和 m m m。这个对应关系是 ( j , l , m ) (j, l, m) (j,l,m) 。
图 7 (a) 表示了将边点作为边缘点对应线的过程
-
假设 i i i 为 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1?中的一个点, i ∈ ε ~ k + 1 i∈\tilde{\varepsilon}_{k+1} i∈ε~k+1?
-
边缘线由两个点表示。假设 j j j 是 i i i 在 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中的最近邻居, j ∈ P ˉ k j∈\bar{\mathcal{P}}_k j∈Pˉk? ,而l是i在两个连续扫描中与 j j j 所在扫描的最近邻居。 ( j , l ) (j,l) (j,l) 构成了 i i i 的对应关系
-
为了验证 j j j 和 l l l 都是边界点,根据(1)检查局部曲面的平滑度(考虑到单个扫描不能包含同一边缘线上的多个点,特别要求 j 和 l 来自不同的扫描)
在边缘线处只有一个例外情况,即边缘线位于扫描平面上。如果是这样的情况,边缘线将会退化成直线并显示在扫描平面上,并且边缘线上的特征点不应被首先提取出来。
图 7 (b) 展示了寻找一个平面点的对应平面片的过程
- 设 i i i 为 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? 中的一个点, i ∈ H ~ k + 1 i∈\tilde{\mathcal{H}}_{k+1} i∈H~k+1?
- 平面片由三个点表示,我们在 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中找到 i i i 的最近邻,表示为 j j j
- 找到另外两个点 l l l 和 m m m 作为 i i i 的最近邻,一个在 j j j 的同一个扫描中,另一个在 j j j 的两个连续扫描之后的扫描中。这确保了这三点不共线
- 为了验证 j , l j,l j,l 和 m m m 都是平面点,再次基于(1)检查局部曲面的光滑度
找到特征点的对应后,现在我们推导出计算特征点到其对应点的距离的表达式。从边缘点开始。对于一个点
i
∈
ε
~
k
+
1
i∈\tilde{\varepsilon}_{k+1}
i∈ε~k+1? ,如果
(
j
,
l
)
(j, l)
(j,l) 是对应的边缘线,
j
,
l
∈
P
ˉ
k
j, l∈\bar{\mathcal{P}}_k
j,l∈Pˉk? ,则可以计算点到线的距离
d
ε
=
∣
(
X
~
(
k
+
1
,
i
)
L
?
X
ˉ
(
k
,
j
)
L
)
×
(
X
~
(
k
+
1
,
i
)
L
?
X
ˉ
(
k
,
l
)
L
)
∣
∣
X
ˉ
(
k
,
j
)
L
?
X
ˉ
(
k
,
l
)
L
∣
(2)
d_{\varepsilon}=\frac{\left|(\tilde{X}^{L}_{(k+1,i)}-\bar{X}^{L}_{(k,j)})\times(\tilde{X}^{L}_{(k+1,i)}-\bar{X}^{L}_{(k,l)})\right|}{\left|\bar{X}^{L}_{(k,j)}-\bar{X}^{L}_{(k,l)}\right|}\tag{2}
dε?=
?Xˉ(k,j)L??Xˉ(k,l)L?
?
?(X~(k+1,i)L??Xˉ(k,j)L?)×(X~(k+1,i)L??Xˉ(k,l)L?)
??(2)
在 { L } \{L\} {L} 中 X ~ ( k + 1 , i ) L \tilde{X}^{L}_{(k+1,i)} X~(k+1,i)L? , X ˉ ( k , j ) L \bar{X}^{L}_{(k,j)} Xˉ(k,j)L? 和 X ˉ ( k , l ) L \bar{X}^{L}_{(k,l)} Xˉ(k,l)L? 分别是点 i 、 j i、j i、j 和 l l l 的坐标
然后,对于一个点
i
∈
H
~
k
+
1
i∈\tilde{\mathcal{H}}_{k+1}
i∈H~k+1? ,如果
(
j
,
l
,
m
)
(j, l, m)
(j,l,m) 是对应的平面块,
j
,
l
,
m
∈
P
ˉ
k
j, l, m ∈\bar{\mathcal{P}}_k
j,l,m∈Pˉk? ,则点到平面的距离为
d
ε
=
∣
(
X
~
(
k
+
1
,
i
)
L
?
X
ˉ
(
k
,
j
)
L
)
(
(
X
ˉ
(
k
,
j
)
L
?
X
ˉ
(
k
,
l
)
L
)
×
(
X
ˉ
(
k
,
j
)
L
?
X
ˉ
(
k
,
m
)
L
)
)
∣
∣
(
X
ˉ
(
k
,
j
)
L
?
X
ˉ
(
k
,
l
)
L
)
×
(
X
ˉ
(
k
,
j
)
L
?
X
ˉ
(
k
,
m
)
L
)
∣
(3)
d_{\varepsilon}=\frac{\left| \begin{matrix} (\tilde{X}^{L}_{(k+1,i)}-\bar{X}^{L}_{(k,j)})\\ ((\bar{X}^{L}_{(k,j)}-\bar{X}^{L}_{(k,l)})\times(\bar{X}^{L}_{(k,j)}-\bar{X}^{L}_{(k,m)})) \end{matrix}\right|}{\left|(\bar{X}^{L}_{(k,j)}-\bar{X}^{L}_{(k,l)})\times(\bar{X}^{L}_{(k,j)}-\bar{X}^{L}_{(k,m)})\right|}\tag{3}
dε?=
?(Xˉ(k,j)L??Xˉ(k,l)L?)×(Xˉ(k,j)L??Xˉ(k,m)L?)
?
?(X~(k+1,i)L??Xˉ(k,j)L?)((Xˉ(k,j)L??Xˉ(k,l)L?)×(Xˉ(k,j)L??Xˉ(k,m)L?))?
??(3)
在 { L } \{L\} {L}中, X ˉ ( k , m ) L \bar{X}^{L}_{(k,m)} Xˉ(k,m)L? 是点 m m m 的坐标
C. 运动估计
激光雷达的运动在一次扫描过程中被建模为恒定的角速度和线速度。使得能够对在不同时间接收到的点在扫描过程中的位姿变换进行线性插值
-
设当前时间戳为 t t t,并记 t k + 1 t_{k+1} tk+1? 为第 k + 1 k+1 k+1 次扫描的起始时间
-
假设 T k + 1 L T^L_{k+1} Tk+1L?是 t k + 1 t_{k+1} tk+1?到 t t t 之间的激光雷达的姿态变换, T k + 1 L T^L_{k+1} Tk+1L?包含激光雷达在六自由度上的刚体运动, T k + 1 L = [ t x , t y , t z , θ x , θ y , θ z ] T T^L_{k+1}=[t_x,t_y,t_z, θ_x, θ_y, θ_z]^T Tk+1L?=[tx?,ty?,tz?,θx?,θy?,θz?]T,其中 t x , t y t_x, t_y tx?,ty?和 t z t_z tz? 分别表示 { L } \{L\} {L} 坐标系沿 x x x、 y y y 和 z z z 轴的平移量, θ x θ_x θx?, θ y θ_y θy?和 θ z θ_z θz? 表示旋转角度,按照右手法则确定
-
给定一个点 i , i ∈ P k + 1 i,i∈\mathcal{P}_{k+1} i,i∈Pk+1?,令 t i t_i ti? 为其时间戳,令 T ( k + 1 , i ) L T^L_{(k+1,i)} T(k+1,i)L? 为 [ t k + 1 , t i ] [t_{k+1}, t_i] [tk+1?,ti?] 之间的位姿变换。 T ( k + 1 , i ) L T^L_{(k+1,i)} T(k+1,i)L? 可以通过 T k + 1 L T^L_{k+1} Tk+1L? 的线性插值来计算
T ( k + 1 , i ) L = t i ? t k + 1 t ? t k + 1 T k + 1 L . (4) T^L_{(k+1,i)}=\frac{t_i-t_{k+1}}{t-t_{k+1}}T^L_{k+1}.\tag{4} T(k+1,i)L?=t?tk+1?ti??tk+1??Tk+1L?.(4) -
为了求解激光雷达运动,我们需要建立 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 和 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1?,或者 H k + 1 \mathcal{H}_{k+1} Hk+1? 和 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? 之间的几何关系
X ( k + 1 , i ) L = R X ~ k + 1 , i L + T k + 1 , i L ( 1 : 3 ) (5) X^L_{(k+1,i)}=R\tilde{X}^L_{k+1,i}+T^L_{k+1,i}(1:3)\tag{5} X(k+1,i)L?=RX~k+1,iL?+Tk+1,iL?(1:3)(5) -
其中 X ( k + 1 , i ) L X^L_{(k+1,i)} X(k+1,i)L? 为 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 或 H k + 1 \mathcal{H}_{k+1} Hk+1? 中 i i i 点的坐标, X ˉ ( k + 1 , i ) L \bar{X}^{L}_{(k+1,i)} Xˉ(k+1,i)L? 为 ε ~ k + 1 \tilde{\varepsilon}_{k+1} ε~k+1? 或 H ~ k + 1 \tilde{\mathcal{H}}_{k+1} H~k+1? 中对应点, T ( k + 1 , i ) L ( a : b ) T^L_{(k+1,i)}(a : b) T(k+1,i)L?(a:b) 是 T ( k + 1 , i ) L T^L_{(k+1,i)} T(k+1,i)L? 的第 a a a 到第 b b b 项, R R R 是由 Rodrigues 公式定义的旋转矩阵
R = e ω ^ θ = I + ω ^ sin ? θ + ω ^ 2 ( 1 ? cos ? θ ) . (6) R=e^{\hat{\omega}\theta}=I+\hat{\omega}\sin\theta+\hat{\omega}^2(1-\cos\theta).\tag{6} R=eω^θ=I+ω^sinθ+ω^2(1?cosθ).(6)
在上式中,θ是旋转的幅度,
θ = ∣ ∣ T ( k + 1 , i ) L ( 4 : 6 ) ∣ ∣ . (7) \theta=\left|\left|T^L_{(k+1,i)}(4:6)\right|\right|.\tag{7} θ= ? ?T(k+1,i)L?(4:6) ? ?.(7)
ω \omega ω 是表示旋转方向的单位向量
ω = T ( k + 1 , i ) L ( 4 : 6 ) / ∣ ∣ T ( k + 1 , i ) L ( 4 : 6 ) ∣ ∣ , (8) \omega=T^L_{(k+1,i)}(4:6)/\left|\left|T^L_{(k+1,i)}(4:6)\right|\right|,\tag{8} ω=T(k+1,i)L?(4:6)/ ? ?T(k+1,i)L?(4:6) ? ?,(8)
ω ^ \hat{\omega} ω^ 是 ω ω ω 的斜对称矩阵 -
结合(2)和(4)-(8),我们可以得出 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 中的边缘点与对应的边缘线之间的几何关系
f ε ( X ( k + 1 , i ) L , T k + 1 L ) = d ε , ?? i ∈ ε k + 1 . (9) f_{\varepsilon}(X^L_{(k+1,i)},T^L_{k+1})=d_{\varepsilon},\ \ i\in{\varepsilon}_{k+1}.\tag{9} fε?(X(k+1,i)L?,Tk+1L?)=dε?,??i∈εk+1?.(9)
结合(3)和(4)-(8),我们可以建立 H k + 1 \mathcal{H}_{k+1} Hk+1? 中的平面点与对应的平面面片之间的另一种几何关系
f H ( X ( k + 1 , i ) L , T k + 1 L ) = d H , ?? i ∈ H k + 1 . (10) f_{\mathcal{H}}(X^L_{(k+1,i)},T^L_{k+1})=d_{\mathcal{H}},\ \ i\in{\mathcal{H}}_{k+1}.\tag{10} fH?(X(k+1,i)L?,Tk+1L?)=dH?,??i∈Hk+1?.(10)
最后用 LevenbergMarquardt 方法求解激光雷达运动。对 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 和 H k + 1 \mathcal{H}_{k+1} Hk+1? 中的每个特征点叠加(9)和(10),得到一个非线性函数
f ( T k + 1 L ) = d , (11) f(T^L_{k+1})=d,\tag{11} f(Tk+1L?)=d,(11) -
其中f的每一行对应一个特征点, d d d 包含相应的距离。计算 f f f 相对于 T k + 1 L T^L_{k+1} Tk+1L? 的雅可比矩阵,记为 J \mathbf{J} J,其中 J = ? f / ? T k + 1 L \mathbf{J} = ?f/?T^L_{k+1} J=?f/?Tk+1L?。然后,可以通过非线性迭代通过将 d d d 最小化为零来求解
T k + 1 L ← T k + 1 L ? ( J T J + λ d i a g ( J T J ) ) ? 1 J T d . (12) T^L_{k+1}\leftarrow T^L_{k+1}-(\mathbf{J}^T\mathbf{J}+\lambda\mathrm{diag}(\mathbf{J}^T\mathbf{J}))^{-1}\mathbf{J}^Td.\tag{12} Tk+1L?←Tk+1L??(JTJ+λdiag(JTJ))?1JTd.(12)
λ \lambda λ 是由 Levenberg-Marquardt 方法确定的因子
D. 激光雷达里程计算法

- 输入:上次扫描的点云 P ˉ k \bar{\mathcal{P}}_k Pˉk?、当前扫描的增长点云 P k + 1 \mathcal{P}_{k+1} Pk+1? 以及上次递归的位姿变换 T k + 1 L T^L_{k+1} Tk+1L?
- 如果开始新的扫描,则 T k + 1 L T^L_{k+1} Tk+1L? 设置为零(第 4-6 行)。然后,算法从 P k + 1 \mathcal{P}_{k+1} Pk+1? 中提取特征点来构造第7行的 ε k + 1 \mathscr{\varepsilon}_{k+1} εk+1? 和 H k + 1 \mathcal{H}_{k+1} Hk+1?
- 对于每个特征点,在 P ˉ k \bar{\mathcal{P}}_k Pˉk? 中找到其对应关系(第 9-19 行)
- 在第 15 行中,算法为每个特征点分配双平方权重。与其对应关系具有较大距离的特征点被分配较小的权重,距离大于阈值的特征点被认为是离群点并被分配零权重
- 在第 16 行,姿势变换更新一次迭代。如果发现收敛或满足最大迭代次数,则非线性优化终止
- 如果算法到达扫描结束,则使用扫描期间的估计运动将 P ˉ k + 1 \bar{\mathcal{P}}_{k+1} Pˉk+1? 重新投影到时间戳 t k + 2 t_{k+2} tk+2?。否则,仅返回变换 T k + 1 L T^L_{k+1} Tk+1L? 进行下一轮递归
6. 激光雷达建图
建图算法的运行频率低于里程计算法,并且每次扫描仅调用一次
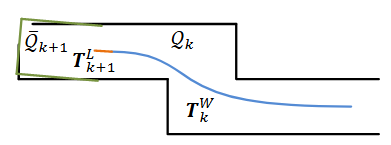
Fig. 8 建图过程的图示。蓝色曲线表示地图上的激光雷达位姿 T k W T^W_k TkW? ,由扫描 k k k 处的建图算法生成。橙色曲线表示扫描 k + 1 k + 1 k+1、 T k + 1 L T^ L_{k+1} Tk+1L? 期间激光雷达的运动,由里程计算法计算。使用 T k W T^W_k TkW? 和 T k + 1 L T^ L_{k+1} Tk+1L? ,将里程计算法发布的未失真点云投影到地图上,表示为 Q k + 1 \mathcal{Q}_{k+1} Qk+1? (绿色线段),并与地图上现有的点云 Q k \mathcal{Q}_k Qk? 进行匹配(黑色线段)。
在扫描 k + 1 k + 1 k+1 结束时,激光雷达里程计生成未失真的点云 P ˉ k \bar{\mathcal{P}}_k Pˉk?,同时生成姿态变换 T k + 1 L T^L_{k+1} Tk+1L? ,其中包含扫描期间的激光雷达运动,介于 [ t k + 1 , t k + 2 ] [t_{k+1} ,t_{k+2}] [tk+1?,tk+2?]。映射算法在世界坐标 { W } \{W\} {W} 中匹配并注册 P ˉ k + 1 \bar{\mathcal{P}}_{k+1} Pˉk+1? ,如图 8 所示。
- 将 Q k \mathcal{Q}_k Qk? 定义为地图上的点云,一直累积到扫描 k k k,并令 T k W T^W_k TkW? 为扫描 k , t k + 1 k,t_{k+1} k,tk+1? 结束时地图上激光雷达的位姿
- 利用激光雷达里程计的输出,映射算法将 T k W T^W_k TkW? 从 t k + 1 t_{k+1} tk+1? 扩展到 t k + 2 t_{k+2} tk+2? 进行一次扫描,以获得 T k + 1 W T^W_{k+1} Tk+1W? ,并将 P ˉ k + 1 \bar{\mathcal{P}}_{k+1} Pˉk+1? 投影到世界坐标 { W } \{W\} {W} ,表示为 Q k + 1 \mathcal{Q}_{k+1} Qk+1?
- 算法通过优化激光雷达位姿 T k + 1 W T^W_{k+1} Tk+1W? 将 Q ˉ k + 1 \bar{\mathcal{Q}}_{k+1} Qˉ?k+1? 与 Q k \mathcal{Q}_k Qk? 进行匹配
特征点的提取方式与第V-A部分相同,但使用了10倍的特征点。为了找到特征点的对应关系,将点云存储在地图 Q k \mathcal{Q}_k Qk? 上 10m 立方区域中。立方体中与 Q ˉ k + 1 \bar{\mathcal{Q}}_{k+1} Qˉ?k+1? 相交的点被提取并存储在 3D KD 树中 。
- 令 S ′ \mathcal{S}' S′ 为周围点的集合。对于边缘点,我们只保留 S ′ \mathcal{S}' S′ 中边缘线上的点,对于平面点,我们只保留平面块上的点
- 然后,我们计算
S
′
\mathcal{S}'
S′ 的协方差矩阵,记为
M
\mathbf{M}
M,以及
M
\mathbf{M}
M 的特征值和特征向量,分别记为
V
\mathbf{V}
V 和
E
\mathbf{E}
E
- 如果 S ′ \mathcal{S}' S′ 分布在一条边缘线上,则 V \mathbf{V} V 包含一个显着大于其他两个的特征值,并且 E \mathbf{E} E 中与最大特征值相关的特征向量表示边缘线的方向
- 另一方面,如果 S ′ \mathcal{S}' S′ 分布在平面贴片上,则 V \mathbf{V} V 包含两个大特征值,第三个特征值明显较小,并且 E \mathbf{E} E 中与最小特征值相关的特征向量表示平面贴片的方向
- 通过穿过 S ′ \mathcal{S}' S′ 的几何中心来确定边缘线或平面斑块的位置
为了计算从特征点到其对应点的距离,选择边缘线上的两个点和平面块上的三个点。这允许使用与 (2) 和 (3) 相同的公式来计算距离。然后,为每个特征点推导方程如(9)或(10),但不同之处在于 Q ˉ k + 1 \bar{\mathcal{Q}}_{k+1} Qˉ?k+1? 中的所有点共享相同的时间戳 t k + 2 t_{k+2} tk+2? 。
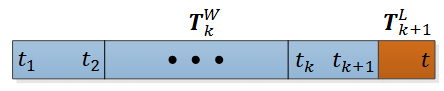
Fig. 9 集成姿态变换。蓝色区域表示来自映射算法的激光雷达姿态 T k + 1 W T^W_{k+1} Tk+1W?,每次扫描生成一次。橙色区域是当前扫描内激光雷达的运动 T k + 1 L T^L_{k+1} Tk+1L? 由里程计算法计算。激光雷达的运动估计是这两个变换的组合,以与 T k + 1 L T^L_{k+1} Tk+1L? 相同的频率进行。
位姿变换的集成如图 9 所示。蓝色区域表示激光雷达映射 T k + 1 W T^W_{k+1} Tk+1W? 的位姿输出,每次扫描生成一次。橙色区域表示激光雷达里程计 T k + 1 L T^L_{k+1} Tk+1L? 的变换输出,频率约为 10Hz。激光雷达相对于地图的位姿是两个变换的组合,其频率与激光雷达里程计相同。
7. 实验
A. 户内与户外测试

Fig. 10 地图生成于 (a)-(b) 狭窄而长的走廊、?-(d) 大型大厅、(e)-(f) 植被道路以及 (g)-(h) 两地之间的果园一排排的树。在室内测试中,激光雷达被放置在推车上,在室外测试中,激光雷达被安装在地面车辆上。所有测试均使用 0.5m/s 的速度。
-
为了评估地图的局部准确性,从相同的环境中收集了第二组激光雷达云。在数据选择期间,激光雷达保持静止并放置在每个环境中的几个不同位置。
-
使用点到平面ICP方法对两个点云进行匹配和比较。匹配完成后,一个点云与第二个点云中对应平面片之间的距离被视为匹配误差

Fig. 11 走廊(红色)、大厅(绿色)、植被道路(蓝色)和果园(黑色)的匹配错误,对应于图10中的四个场景。
-
户内的误差比户外的误差小。自然环境中存在很多其他的干扰
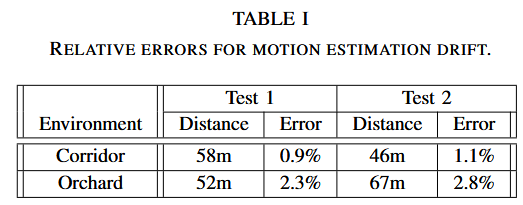
此外,本文还进行测试来测量运动估计的累积漂移。运动从的起始位置和结束位置是相同的,运动估计会在起始位置和结束位置之间产生间隙,该间隙指示漂移量。
B. 利用IMU辅助
以两种方式对点云进行预处理
- 使用 IMU 的方向,将一次扫描中接收到的点云旋转以与该扫描中激光雷达的初始方向对齐
- 使用加速度测量,运动失真被部分消除,就好像激光雷达在扫描过程中以恒定速度移动一样。然后,点云由激光雷达里程计和测绘程序进行处理
IMU 方向是通过对卡尔曼滤波器中陀螺仪的角速率和加速度计的读数进行积分来获得的。
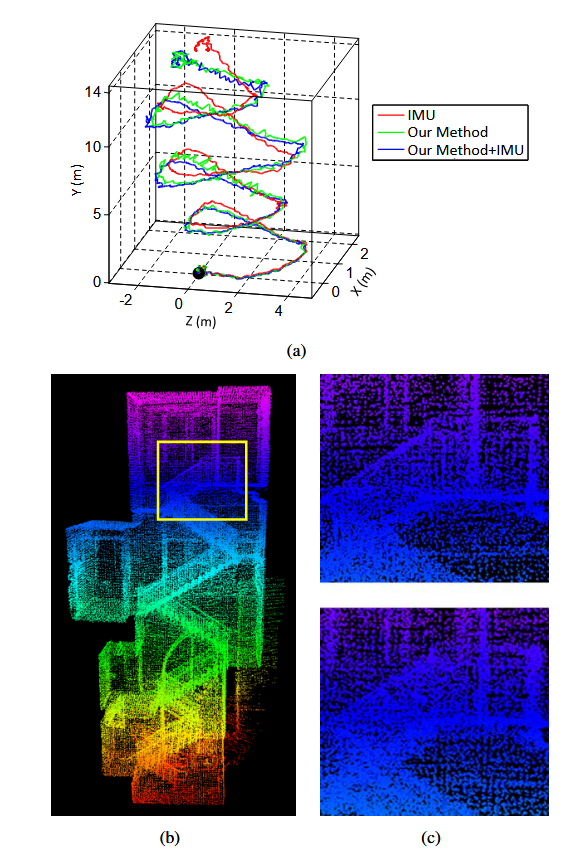
Fig. 12 有无 IMU 辅助的结果比较。一个人拿着激光雷达走在楼梯上。黑点是起点。在 (a) 中,红色曲线是使用 IMU 的方向和我们的方法估计的平移来计算的,绿色曲线仅依赖于我们方法中的优化,蓝色曲线使用 IMU 数据进行预处理,然后再进行该方法。(b) 是蓝色曲线对应的图。在(c)中,上图和下图分别对应于蓝色和绿色曲线,使用(b)中黄色矩形标记的区域。上图中的边缘更锐利,表明地图上的精度更高。
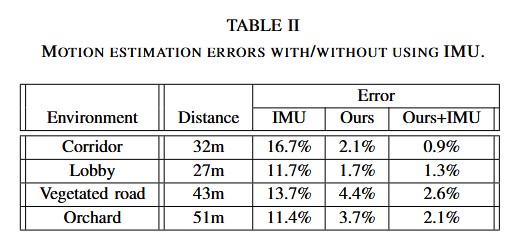
表 II 比较了使用和不使用 IMU 时运动估计的相对误差
C. KITTI数据集测试
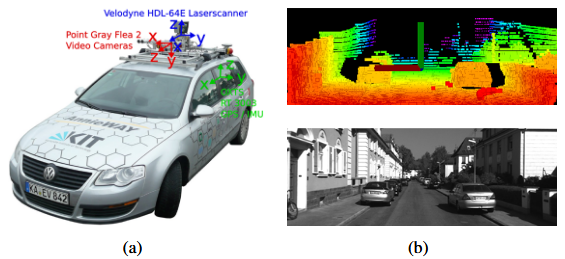
Fig. 13 (a) KITTI 基准测试使用的传感器配置和车辆。该车辆安装了 Velodyne 激光雷达、立体摄像机和用于地面实况采集的高精度 GPS/INS。我们的方法仅使用 Velodyne 激光雷达的数据。 (b) 城市场景中的激光雷达云样本(上图)和相应的视觉图像(下图)。
数据集主要涵盖三类环境:周围有建筑物的“城市”、场景中有植被的小道路上的“乡村”以及道路宽阔且周围环境相对干净的“高速公路”。
8. 总结和展望
该方法通过并行运行的两种算法来划分和解决问题:
- 激光雷达里程计进行粗略处理以估计较高频率的速度
- 激光雷达测绘则执行精细处理以以较低频率创建地图
两种算法的配合可以实现准确的实时运动估计和建图
此外,该方法可以利用激光雷达扫描模式和点云分布。进行特征匹配是为了确保里程计算法中的快速计算,并增强建图算法中的准确性
限制:由于当前的方法无法识别环路闭合,因此未来的工作包括开发一种通过闭合环路来修复运动估计漂移的方法。此外,将把本文方法的输出与卡尔曼滤波器中的 IMU 集成,以进一步减少运动估计漂移。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!