详解一次一密

目录

一. 介绍

二. 一次一密方案

三. 正确性分析

四. 证明一次一密方案是完美安全

五. 一次一密的应用

六. 小结

---

一. 介绍

一次一密，英语写做one time pad。

在1917年，Vernam提出了一个完美安全的加密方案，后世将其称之为一次一密。在当时，完美安全的概念还没有引出，大约25年后，Shannon提出了完美安全的定义，并且证明了一次一密是符合完美安全的（perfect secrecy）。

假定a为长度为l的比特串，如下：

同理有个相同长度的比特串b，如下：

两者的异或运算，写做bitwise exclusive，也就是XOR运算，如下：

在一次一密方案中，密钥，消息，密文的长度均相等。并且要求密钥是均匀且随机的比特串，紧跟着对密钥和密文做异或运算即可以得到密文。

二. 一次一密方案

固定一个整数l>0，消息，密钥和密文均为长度l的比特串。也就是消息空间M，密钥空间K和密文空间C，均为：

(1)Gen密钥生成算法

密钥生成算法会根据均匀分布，从密钥空间K中选择一个密钥。密钥空间为，所以每个密钥被选择的概率都是相等的，均为：

（2）Enc加密算法、

给定一个密钥k和一个明文m，格式均满足：

加密算法可计算密文如下：

（3）Dec解密算法

给定一个密钥k和密文c，格式均满足：

解密算法可计算得到明文，如下：

三. 正确性分析

对于任意的密钥k和消息m，我们都可以得到：

很显然，一次一密的方案是正确的。

四. 证明一次一密方案是完美安全

无论明文是什么，如果都能证明密文是均匀分布的，则可以说明一次一密方案是完美安全的。接下里，我们将利用一种严格的形式来证明完美安全性。

对于任意明文m是可取的，也就是Pr[M=m]>0，我们来看此时密文的分布情况：

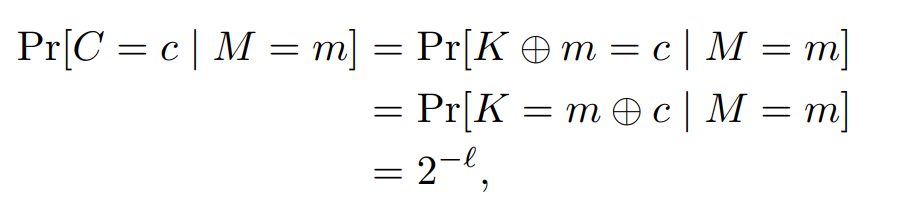
第一个等号：方案对加密的定义，要注意此时明文为m是固定的

第二个等号：异或运算的性质；

第三个等号：密钥K是均匀且随机分布的l比特串，且跟M无关，所以可计算其概率。

接着我们来计算密文为c的概率：

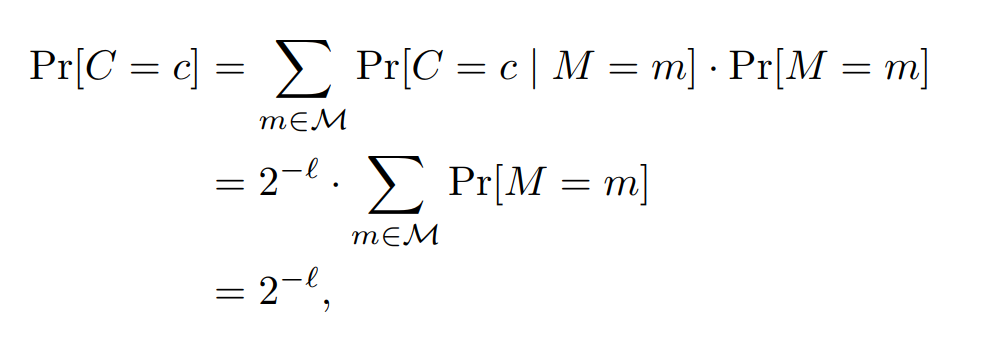
第一个等号：考虑所有明文的情况；

第二个等号：刚才的结论；

第三个等号：求和概率

接着利用Bayes定理，也就是条件概率，可计算为：

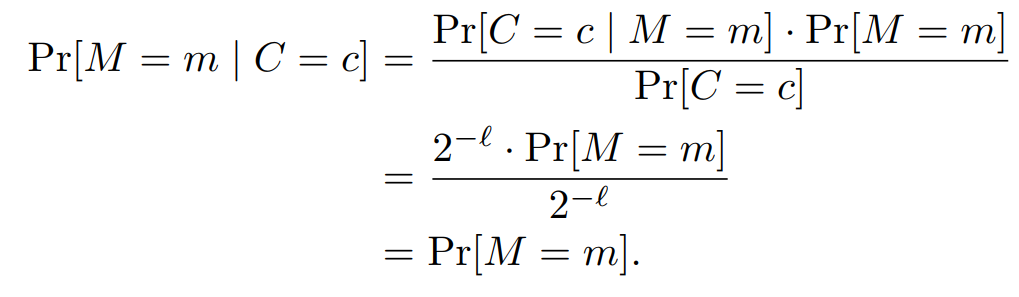
第一个等号：条件概率的性质

第二个等号：带入以上计算结果

第三个等号：化简

根据以上可得已知密文对明文没有任何的影响，所以该方案为完美安全的。

五. 一次一密的应用

在20世纪中期，一次一密方案被应用于很多国家情报机构（national intelligence agency），主要用来加密对时间敏感的数据。比如，白宫（white house）和克里姆林宫（Kremlin）在冷战时期的通信就通过“红电话”。US和USSR的政府机构可以借助可信的通讯员来交换很长的密钥，把随机的字母写在纸张上。

一次一密方案的安全性非常好，但是在网络安全中如今并不常见，其还是有很多的限制。比如，方案中我们要求密钥的长度和明文的长度一样，在加密很长的消息时，则不太实用。而且，往往合法的通信双方是无法提取预测具体消息的长度。

一次一密方案要求密钥k只能使用一次。如果使用同一个密钥来加密多个消息，会出现什么情况？比如我们假设消息m和m'都是使用k来进行加密的，此时我不知道具体的k是什么，但首先我们知道密文格式为：

由此可计算：

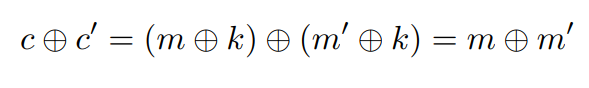
也就是m和m'的异或结果信息会被泄露，换句话说就是两个消息的区别则被获取。如果对多个消息的加密使用同一个密钥的话，那么该方案肯定不符合完美安全的要求，只要其相同消息足够多，那么借助频率攻击法，很有可能解密出明文。

历史上，VENONA项目就分析过此类的安全性。曾经，前苏联（Soviet Union）在几十年内就重复使用过密钥，美国（US）和英国（UK）就解密出明文。

六. 小结

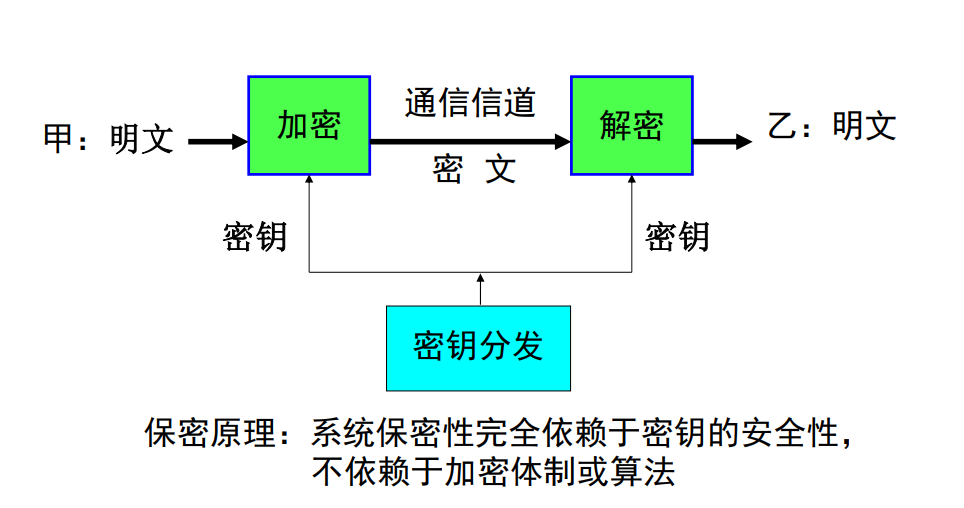
在现代密码学中，保密原理指的是，系统保密性完全依赖于密钥的安全性，不依赖于加密体制或算法。

然而现有的保密通信体系不存在无条件安全的方案来分发密钥，这个过程是很难实现的。现代密码学常用对称密码体制和公钥密码体制：

• 对称密钥体制：也被称之为私钥密码，比如使用AES（高等数据加密标准）等进行密钥扩张和分配
• 非对称密钥体制：也被称之为公钥密码，比如使用基于大整数因子分解问题的RSA体制和Rabin体制、基于有限域上或者基于椭圆曲线上的离散对数问题的Diffie-Hellman公钥体制和ElGamal体制。然而这些体制均依赖于数学计算复杂性，并不是无条件安全的，而且其依赖的数学难问题并不是不可解决的。

常规体制不存在多项式算法复杂性的假设并未得到证明。所以我们常说密码学使用的是一种假设的安全，也就是目前不存在算法可以解决某些困难问题，至于以后有没有可能被解决那就不得而知了。

目前，长达1024比特长度的RSA体制已经被破解。

基于Hash函数的世界通行密码标准系列算法MD5等被王小云教授等人破解。

Shor的大数分解量子算法可以以低的复杂性破解RSA体制（例如，1分钟就可以破解1024比特RSA）

使用穷举破译法，量子计算机能够进行把 复杂性降低。