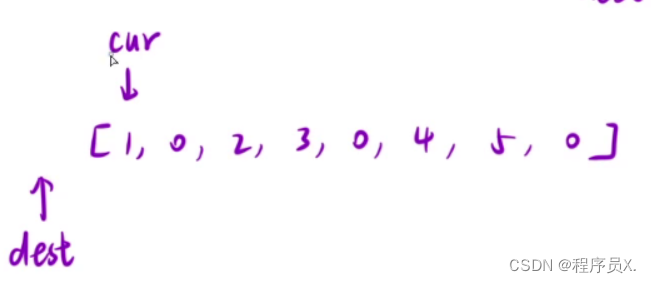双指针算法

目录

目录

一、移动零(283. 移动零 - 力扣（LeetCode）) 简单题

二、复写零（1089. 复写零 - 力扣（LeetCode））简单题

三、快乐数（202. 快乐数 - 力扣（LeetCode））简单题

四、盛最多水的容器（11. 盛最多水的容器 - 力扣（LeetCode））中等题

五、有效三角形的个数（611. 有效三角形的个数 - 力扣（LeetCode））中等题

六、三数之和（15. 三数之和 - 力扣（LeetCode））中等题

七、四数之和（18. 四数之和 - 力扣（LeetCode））中等题

总结

---

一、移动零(283. 移动零 - 力扣（LeetCode）) 简单题

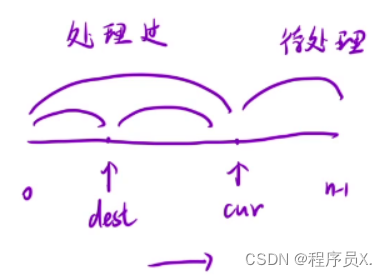
1. 通过三重数组划分，dest之前是不为0的数，dest - cur 是为0的数， cur - arr.length 是未处理的数
2. 让 dest 从 -1 开始，cur 从 0 开始，遇到不为 0 的数，先让dest++，然后让 cur 位置的数和 dest 位置的数交换，然后让cur++，以此循环，直到cur > arr.length，即可完成零的移动；

代码如下：

class Solution {
    public void moveZeroes(int[] nums) {
        int dest = -1;
        int cur = 0;
        while(cur < nums.length){
            if(nums[cur] != 0){
                int t = nums[++dest];
                nums[dest] = nums[cur];
                nums[cur] = t;
            }
            cur++;
        }
    }
}

---

二、复写零（1089. 复写零 - 力扣（LeetCode））简单题

1、先通过双指针从前往后找到最后一个需要复写的数

• 让 cur 从 0开始，dest 从 -1 开始
• 先判断cur位置的值是否为0
• cur位置的值不为0，dest指针移动一步，反之则移动两步
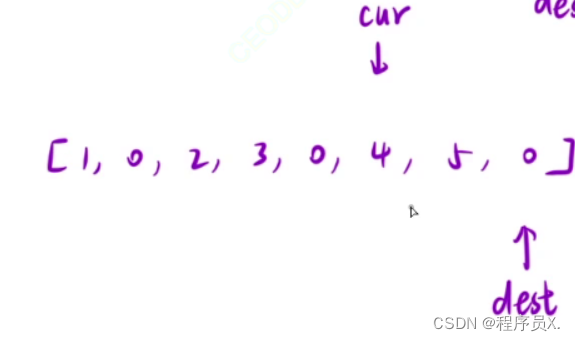
• 再判断一下dest指针是否到达结束位置arr.length - 1
• 如果未到达则让 cur++ ，到达则直接 break 退出循环

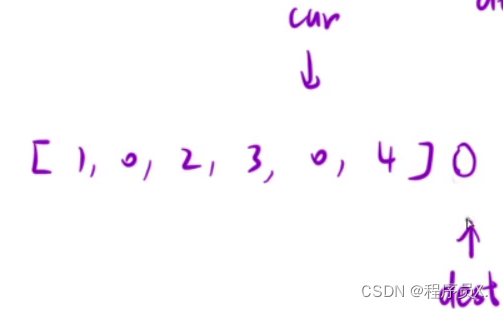
2、处理边界情况（当cur为0时，dest出现越界情况）

单独处理这种情况，当arr[cur] == 0时，arr[arr.length - 1] = 0, cur --, dest -= 2。

3、从后向前完成复写操作

代码如下：

class Solution {
    public void duplicateZeros(int[] arr) {
        // 找到复写的最后一个数
        int dest = -1;
        int cur = 0;
        while(true){
            if(arr[cur] == 0){
                dest += 2;
            }else{
                dest++;
            }
            if(dest >= arr.length - 1){
                break;
            }
            cur++;
        }
        // 处理特殊情况，最后一个复写的数为0,dest 则会出现越界
        if(dest == arr.length){
            arr[arr.length - 1] = 0;
            dest -= 2;
            cur--;
        }
        // 进行从后往前的复写0操作
        while(cur >= 0){
            if(arr[cur] == 0){
                arr[dest--] = 0;
                arr[dest--] = 0;
            }else{
                arr[dest--] = arr[cur];
            }
            cur--;
        }
    }
}

---

三、快乐数（202. 快乐数 - 力扣（LeetCode））简单题

解法：判断这个循环中是否有环（通过鸽巢原理可以证明其一定有环），使用快慢指针算法；

• 定义快慢指针
• 慢指针每次移动一步，快指针每次移动两步
• 判断相遇时的值是否为题中规定的值

代码如下：

class Solution {
    public static int get(int n){
        int sum = 0;
        while(n > 0){
            int a = n % 10;
            sum += a * a;
            n /= 10;
        }
        return sum;
    }
    public boolean isHappy(int n) {
        int slow = n;
        int fast = get(n);
        while(slow != fast){
            slow = get(slow);
            fast = get(fast);
            fast = get(fast);
        }
        return slow == 1;
    }
}

---

四、盛最多水的容器（11. 盛最多水的容器 - 力扣（LeetCode））中等题

利用双指针的单调性解决问题

• 定义两个指针，一个 l 从 0 开始往后走，一个 r 从 arr.length - 1 开始往前走
• 确认公式：面积 = 长 * 宽
• 从图中易知长为 r - l，宽为两个下标对应的数的最小值（arr[l]、arr[r] ），因为装水看得是谁最短就只能装到那个位置
• 我们需要找到最大的面积，就需要舍去短的宽度，所以每次如果 arr[l] < arr[r] ，我们就需要让 l++ 去寻找下一个长的 arr[l]，反之如果arr[l] > arr[r] ，我们则需要向前寻找长的arr[r]
• 通过全局变量sum 记录寻找过程中的最大值，当l 和 r相遇时即可结束循环，完成最大容器的寻找；

class Solution {
    public int maxArea(int[] height) {
        int sum = 0;
        int l = 0;
        int r = height.length - 1;
        while(l < r){
            int t = 0;
            if(height[l] < height[r]){
                t = height[l] * (r - l);
                l++;
            }else{
                t = height[r] * (r - l);
                r--;
            }
            if(t > sum){
                sum = t;
            }
        }
        return sum;
    }
}

---

五、有效三角形的个数（611. 有效三角形的个数 - 力扣（LeetCode））中等题

利用单调性，通过双指针算法解决

• 先将数组排序，保证单调性
• 先固定最大的数(max)，寻找其他两个数（确定三角形的方法：a + b > c）
• 在最大的数左侧区间使用双指针，从最开始（l = 0）和最大的数小一点的数（r = max - 1）的位置开始检测是否符合要求
• 如果当 l = 0，r = max - 1时，arr[l] + arr[r] > arr[max]，我们即可确认（l - r） 中的所有数都符合要求（因为经过排序， arr[l]是整个数组中最小的数，最小的数都满足大于了，后面的数自然也就满足了），即可让 r-- ，尝试让小一点的数来检测是否符合要求
• 如果arr[l] + arr[r]
• 当 l 和 r 相遇时，即可找到固定max的区间内的所有情况
• 最后让 max--，继续寻找满足要求的数

代码如下：

class Solution {
    public int triangleNumber(int[] nums) {
        // 排序数组，保证单调性
        Arrays.sort(nums);
        int count = 0;
        int max = nums.length - 1;
        // 固定最大的数
        while(max >= 0){
            int l = 0;
            int r = max - 1;
            // 使用双指针快速统计出符合三元组要求的数
            while(l < r){
                if(nums[l] + nums[r] <= nums[max]){
                    l++;
                }else{
                    count += r - l;
                    r--;
                }
            }
            max--;
        }
        return count;
    }
}

---

六、三数之和（15. 三数之和 - 力扣（LeetCode））中等题

通过排序+双指针算法解决

• 先将数组排序，确认单调性（便于去重）
• 固定一个数 max，然后去寻找其他两个数
• 在max 左侧区间通过双指针算法寻找其他两个数
• 通过题目中公式我们可知，nums[l] + nums[r] < -nums[max] 时，l++，相反 r--，如果nums[l] + nums[r] == -nums[max]，则需要将这三个数一起放入list集合中，最后让 l ++，r --
• 注意去重问题：因为前面使用了排序算法，使得数组有序，所以在保证 （l < r）的大前提下，当我们从左往右找的时候发现 nums[l] == nums[l - 1] 时，就出现重复数字了，直接让 l++；相同的是 当从右往左找的时候发现 nums[r] == nums[r + 1] 时，出现重复数字，直接让 r--；注意我们固定的数 max，先让max--，然后在保证max >= 0 的前提下，保证发现 nums[max] == nums[max + 1]时，让 max--；以上去重都需要使用while循环解决，因为可能出现多个重复数字在一起
• 最后将list集合的三个数字存入sum集合中，即可解决问题

代码如下：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        // 排序保证单调性
        Arrays.sort(nums);
        int max = n - 1;
        List<List<Integer>> sum = new ArrayList<>();
        // 固定一个数，寻找其他两个数
        while(max >= 0){
            // 小优化
            if(nums[max] < 0) break;
            int l = 0;
            int r = max - 1;
            int x = -nums[max];
            // 使用双指针算法寻找其他两个数
            while(l < r){
                if(nums[l] + nums[r] < x){
                    l++;
                }else if(nums[l] + nums[r] > x){
                    r--;
                }else{
                    // 将找到的三个数加入集合中
                    List<Integer> t = new ArrayList<>();
                    if(nums[l] + nums[r] == x){
                        t.add(nums[l]);
                        t.add(nums[r]);
                        t.add(nums[max]);
                        l++;
                        r--;
                        // 去重
                        while(l < r && nums[l] == nums[l - 1]){l++;}
                        while(l < r && nums[r] == nums[r + 1]){r--;}
                    }
                    sum.add(t);
                }
            }
            max--;
            // 去重
            while(max >= 0 && nums[max] == nums[max + 1]){max--;}
        }
        return sum;
    }
}

---

七、四数之和（18. 四数之和 - 力扣（LeetCode））中等题

解法和上面三数之和一样，只是需要多固定一个数和多去重一个数罢了

代码如下：

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> sum = new ArrayList<>();
        Arrays.sort(nums);
        // 固定最后一个数
        int m = nums.length - 1;
        while(m >= 0){
            // 固定倒数第二个数
            int n = m - 1;
            while(n >= 0){
                // 使用双指针算法进行寻找最后两个数
                int l = 0;
                int r = n - 1;
                long x = (long)target - nums[m] - nums[n];
                while(l < r){
                    if(nums[l] + nums[r] < x){
                        l++;
                    }else if(nums[l] + nums[r] > x){
                        r--;
                    }else{
                        List<Integer> t = new ArrayList<>();
                        t.add(nums[l]);
                        t.add(nums[r]);
                        t.add(nums[n]);
                        t.add(nums[m]);
                        l++;
                        r--;
                        // 进行去重
                        while(l < r && nums[l] == nums[l - 1]){l++;}
                        while(l < r && nums[r] == nums[r + 1]){r--;}
                        sum.add(t);
                    }
                }
                n--;
                while(n >= 0 && nums[n] == nums[n + 1]){n--;}
            }
            m--;
            while(m >= 0 && nums[m] == nums[m + 1]){m--;}
        }
        return sum;
    }
}

---

总结

双指针算法贯穿算法学习之路，是基础中的重中之重，需要多练，多练就有思路，也是很多其他中等困难题的有效优化手段，需要多刷题练习。