【数据结构】手把手分析：链式二叉树的实现

---

前言

?? 树状结构是数据结构中非常重要的部分，我们在进行对树的学习时，一般都是通过二叉树来学习树状结构。但我们知道，这里的二叉树不是完全二叉树，使用数组存储的话会产生较大的空间浪费，我们通常只把堆使用顺序结构的数组来存储。所以我们在实现二叉树的时候一般都是采用链式结构。
??文章末尾附带完整源码。

一、二叉树的概念

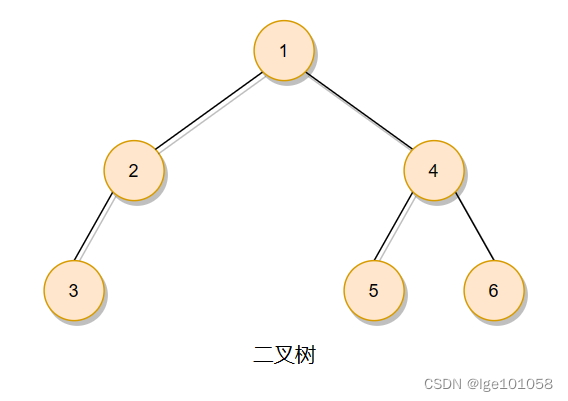
??一棵二叉树是结点的一个有限集合该集合：
???? 1.或者为空
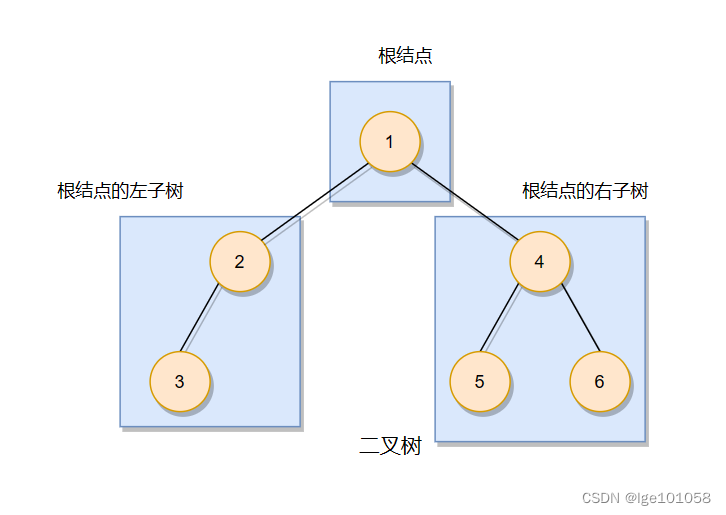
???? 2.由一个根节点加上两棵别称为左子树和右子树的二叉树组成


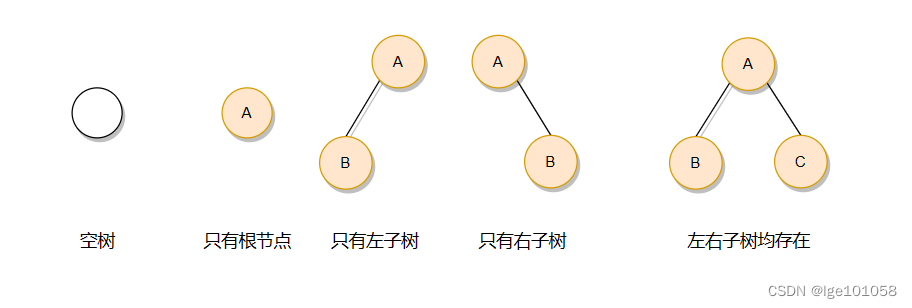
??注意：对于任意的二叉树都是由以下几种情况复合而成的：

二、链式二叉树的存储

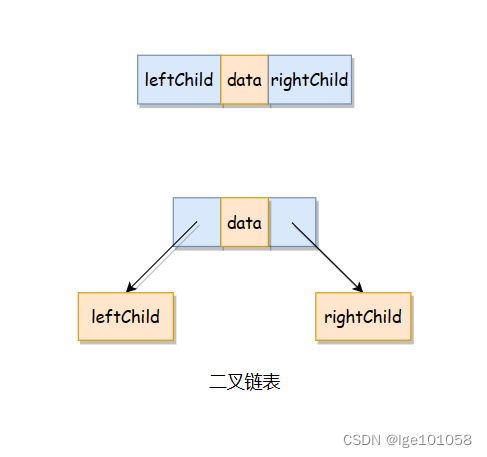
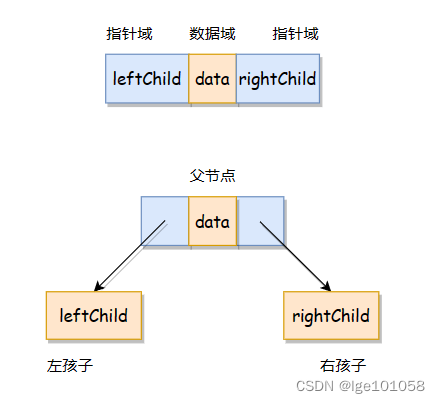
??顾名思义，链式二叉树就是采用链式存储，使用指针指向孩子节点。我们可以使用以下两种方式存储：
??1、没有指向父节点的指针

??2、有指向父节点的指针

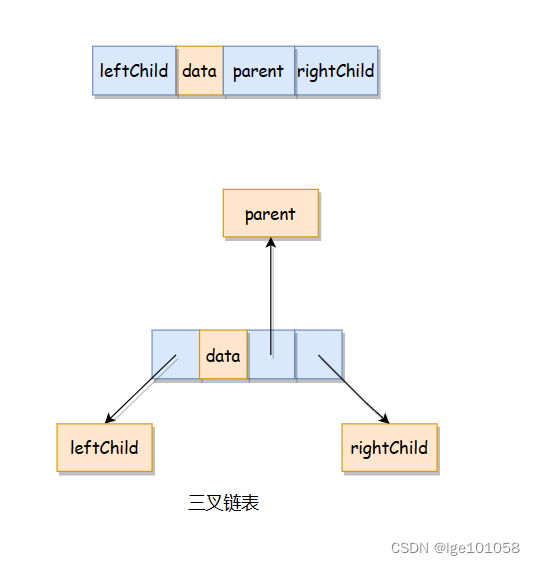
??由于这两种并没有本质上的区别，所以我们采用没有指向父节点的指针的二叉链表来实现。

三、二叉树的遍历

??二叉树有四种遍历方式，分别是1.前序遍历，2.中序遍历，3.后序遍历，4.层序遍历。其中，层序遍历稍微有点麻烦，需要使用队列的存储结构。为避免文章篇幅过长，层序遍历将不在本篇介绍。
??在这三种遍历当中，“前”，“中”，“后”的意思都是对于所有树或者子树的根结点，也可以理解为任意一个父结点与其孩子的先后顺序。先说一句，左孩子的顺序是一定在右孩子的前面的，于是，三种遍历的顺序就是：

??前序遍历：“根结点” - - “左孩子结点” - - “右孩子结点”
??中序遍历：“左孩子结点” - - “根结点” - - “右孩子结点”
??后序遍历：“左孩子结点” - - “右孩子结点” - - “根结点”

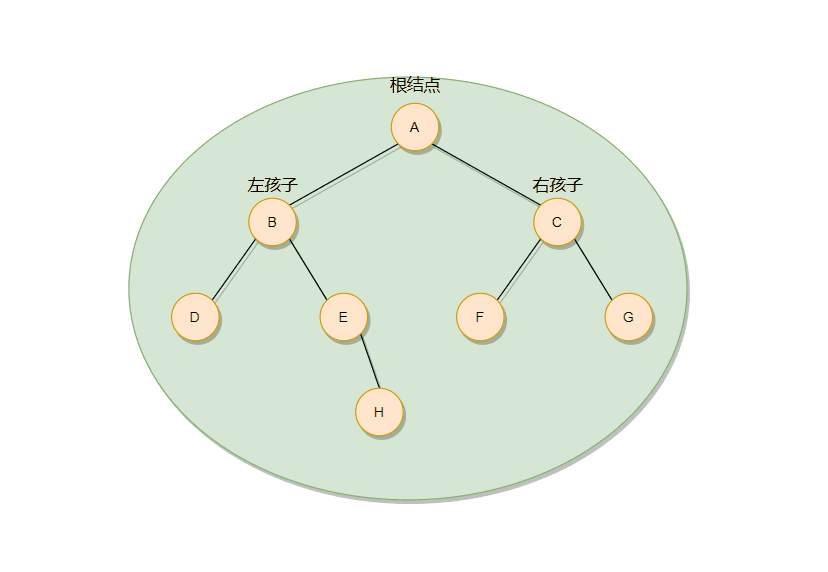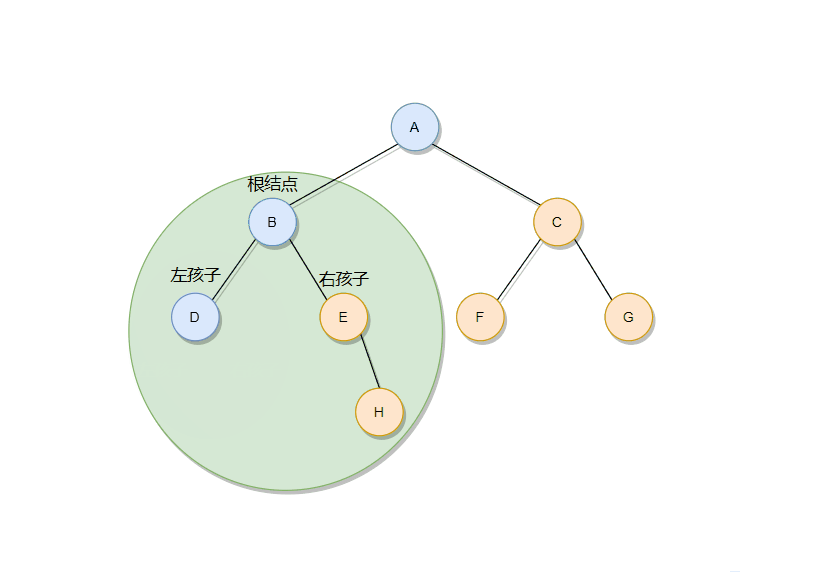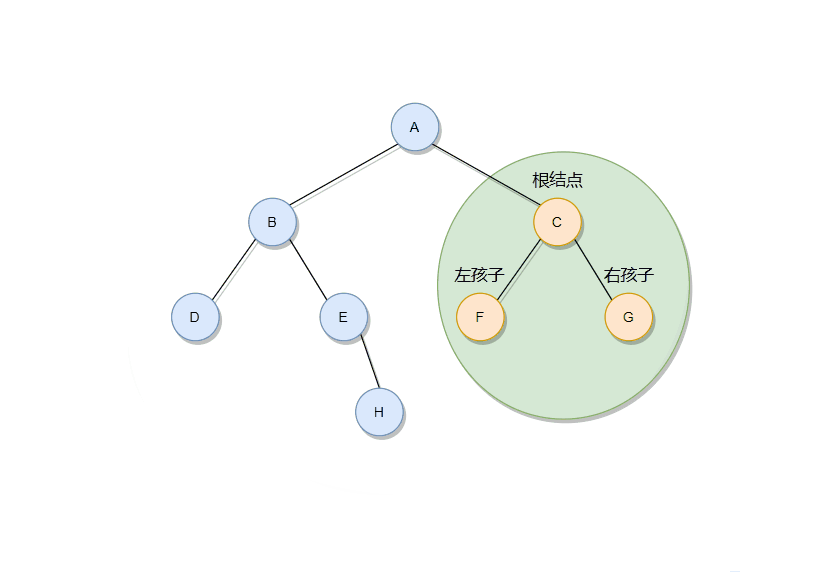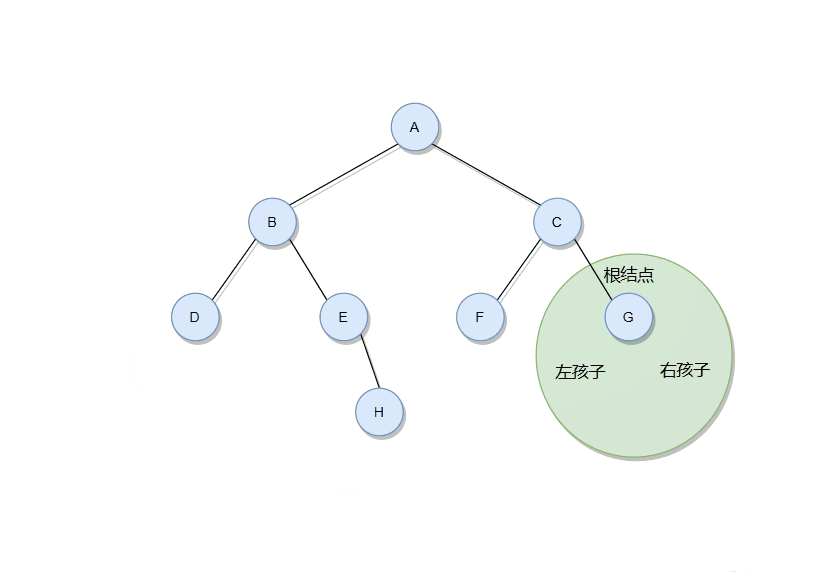
??我们在此以中序遍历举个例子。假设有一棵树如下图：

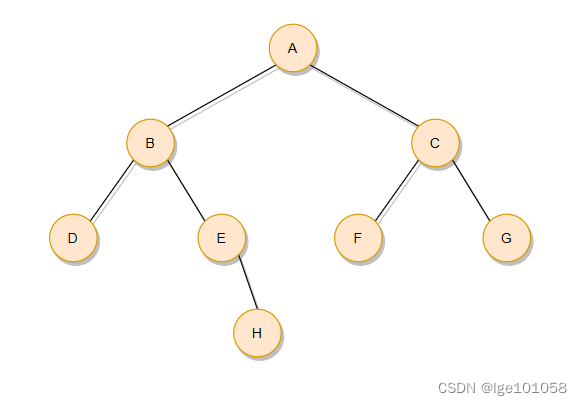
??中序遍历的要点就是，在每一颗树或者子树当中，左孩子结点都必须在根结点的前面，根结点必须在右孩子结点前面。

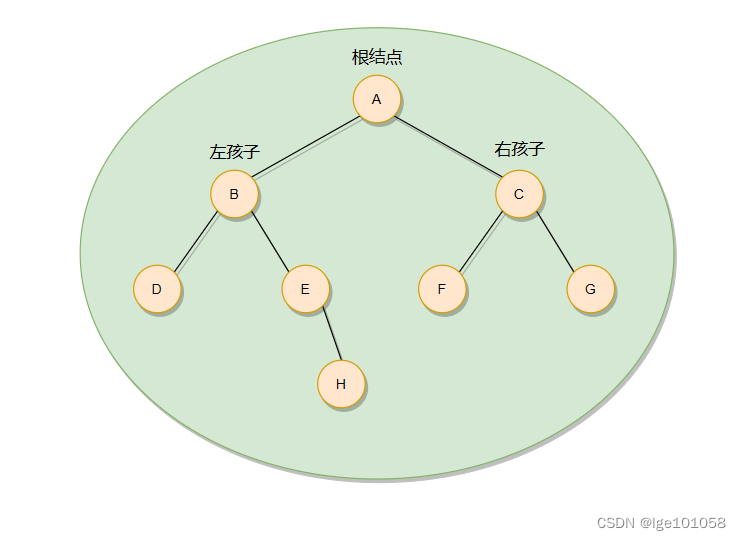
??由图可知，在整颗二叉树中， ‘B’ 结点要在 ‘A’ 结点前面， ‘A’ 结点要在 ‘C’结点前面。所以 ‘B’ 结点就是第一个吗？当然不是！还要考虑子树！

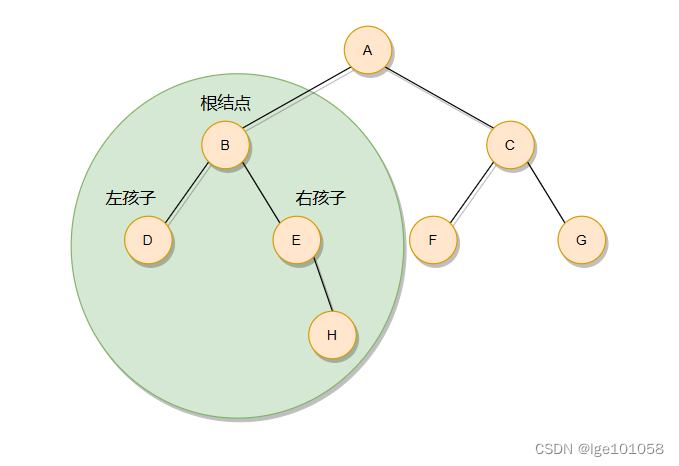
??由上图可知，在当前子树当中， ‘B’ 结点成根结点了，需要在左孩子结点 ‘D’ 的后面。又由于 ‘D’ 结点没有孩子结点，所以终于轮到了 ‘B’ 结点，然后才能考虑右孩子结点，在考虑右孩子结点的时候同样不能忘记考虑子树情况。
??于是，该树的中序遍历得到的结果应该是：DBEHAFCG 。咱们将空值以 ‘#’ 的形式插入当中，就是：#D#B#E#H#A#F#C#G# 。

四、头文件的编写

??为了使代码可读性高，功能模块化，我们将不同的代码分开在不同的文件下。首先我们创建一个头文件，叫做 “BinaryTree.h” 。

1.引入库函数头文件

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

2.定义链式二叉树结构体

// 宏定义数据类型
typedef char BTDataType;

// 二叉树的结构体
typedef struct BinaryTreeNode
{
    // 数据域
	BTDataType data;
	// 指向左孩子的指针域
	struct BinaryTreeNode* left;
	// 指向右孩子的指针域
	struct BinaryTreeNode* right;
}BTNode;

??这里创建的结构体跟刚刚的二叉链表完全一样，任意一个节点都有包含数据值的数据域和两个指向孩子的指针域。

3.声明功能函数

// 以前序遍历的方式构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);
// 二叉树销毁
void BinaryTreeDestroy(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);

五、主函数文件的编写

??我们创建一个源文件，叫做 “test.c” 。

1.包含头文件

#include"BinaryTree.h"

2.编写测试用例

void test()
{
    // 用前序遍历的方式构建创建二叉树节点顺序，其中‘#’代表空的意思
	char a[] = "ABD##E#H##CF##G##";
	// 用作遍历数组
	int b = 0;
	// 根据数组构建二叉树
	BTNode* root = BinaryTreeCreate(a, &b);
	// 结点个数
	printf("结点个数：%d\n", BinaryTreeSize(root));
	// 叶子结点个数
	printf("叶子结点个数：%d\n", BinaryTreeLeafSize(root));
	// 第k层结点个数
	printf("第k层结点个数：%d\n", BinaryTreeLevelKSize(root, 2));
	// 值为x的结点的地址
	printf("值为F的结点的地址：%p\n", BinaryTreeFind(root, 'F'));
	// 前序遍历
	printf("二叉树的前序遍历：");
	BinaryTreePrevOrder(root);
	printf("\n");
	// 中序遍历
	printf("二叉树的中序遍历：");
	BinaryTreeInOrder(root);
	printf("\n");
	// 后序遍历
	printf("二叉树的后序遍历：");
	BinaryTreePostOrder(root);
	printf("\n"); 
	// 销毁二叉树
	BinaryTreeDestroy(root);
	// 销毁空间后，指针置空
	root = NULL;
}

??由于二叉树的层序遍历以及判断二叉树是否为完全二叉树均需要使用队列结构，为避免篇幅过长，这两个函数将不在此实现。

3.编写主函数

int main()
{
    // 调用测试用例
	test();
	return 0;
}

??以上测试用例可以根据自身情况修改。

六、功能函数的编写

??我们创建一个源文件，叫做 “BinaryTree.c” 。

1.包含头文件

#include"BinaryTree.h"

2.构建二叉树

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
    // 如果数组第*pi的值为‘#’，说明遇到了空结点，说明该结点不存在
	if (a[*pi] == '#')
	{
	    // 准备查看数组的下一个元素
		++(*pi);
		// 返回空
		return NULL;
	}

    // 如果当前值不为空
    // 为当前结点开辟一个新的二叉树结构体大小的空间
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	// 开辟空间失败
	if (!root)
	{
	    // 弹出反馈
		perror("malloc fail");
		// 退出程序
		exit(-1);
	}

    // 开辟空间成功
    // 将当前的数组的值赋值给该结点的数据域，并让*pi增加1，准备查看下一个数组元素
	root->data = a[(*pi)++];
	// 递归传回该结点的左孩子的地址
	root->left = BinaryTreeCreate(a, pi);
	// 递归传回该结点的右孩子的地址
	root->right = BinaryTreeCreate(a, pi);
	// 返回当前结点的地址
	return root;
}

??其实在对链式二叉树的学习当中，递归思想是非常重要的，在上面函数里，遇到空返回不多说，在遇到不为空的值时，说明遇到了可以成为结点的数据，又因为我们这是前序遍历构建二叉树，先遍历的是根结点，所以我们要先开辟根结点的空间，再给根结点赋值，总之先把根结点的工作都做完，最后再去递归左孩子和右孩子。

3.二叉树的销毁

void BinaryTreeDestroy(BTNode* root)
{
    // 空结点直接返回
	if (!root)
		return;
	
	// 递归左孩子
	BinaryTreeDestroy(root->left);
	// 递归右孩子
	BinaryTreeDestroy(root->right);
	// 销毁根结点
	free(root);
}

??在二叉树的销毁当中，同样是使用遍历来销毁，但是销毁了一个结点后就无法通过该结点去找到该结点的左孩子和右孩子，因此，必须要把左孩子和右孩子都销毁完了后才能销毁父结点。所以销毁必须要使用后序遍历。

4.二叉树的结点个数

int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

??二叉树的结点个数比较好算，因为二叉树的结点个数就是左子树的结点个数加上右子树的结点个数最后加上根结点本身的一个结点就是整棵树的结点个数，子树同样可以递归下去。

5.二叉树的叶子节点个数

int BinaryTreeLeafSize(BTNode* root)
{
    // 空结点直接返回0个叶子节点
	if (!root)
		return 0;
    // 记录左子树的叶子结点个数
	int leftSize = BinaryTreeLeafSize(root->left);
	// 记录右子树的叶子结点个数
	int rightSize = BinaryTreeLeafSize(root->right);
	// 返回左右子树叶子结点个数的总和，如果没有结点说明自己是叶子结点
	return leftSize + rightSize == 0 ? 1 : leftSize + rightSize;
}

??二叉树的叶子结点的含义就是该结点没有左右孩子，于是可以通过计算每个结点的孩子个数，如果一个结点它没有孩子，说明它就是叶子结点，然后递归叶子结点个数回去。

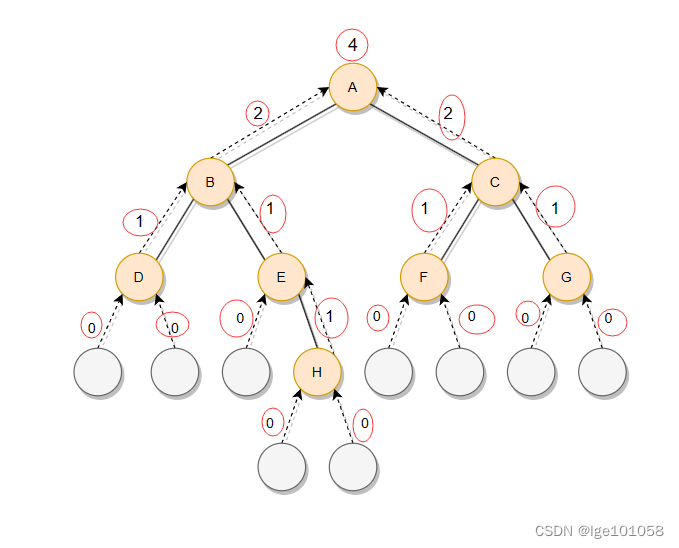
6.二叉树第k层的结点个数

int BinaryTreeLevelKSize(BTNode* root, int k)
{
    // 空结点或者超过k层直接返回0
	if (!root || k < 1)
		return 0;
	// 该根结点的左子树中含有第k层结点的个数
	int leftSize = BinaryTreeLevelKSize(root->left, k - 1);
	// 该根结点的右子树中含有第k层结点的个数
	int rightSize = BinaryTreeLevelKSize(root->right, k - 1);
	// 当k为1时，说明到达了k层，
	return k == 1 ? leftSize + rightSize + 1 : leftSize + rightSize;
}

??同样的方法，使用递归，不断把已经获取到的需要求的结点个数往回传。递归的停止条件在找到空间点之外多了一条已经超过了第k层。这样就能正确递归到第k层的位置，然后返回结点个数即可。

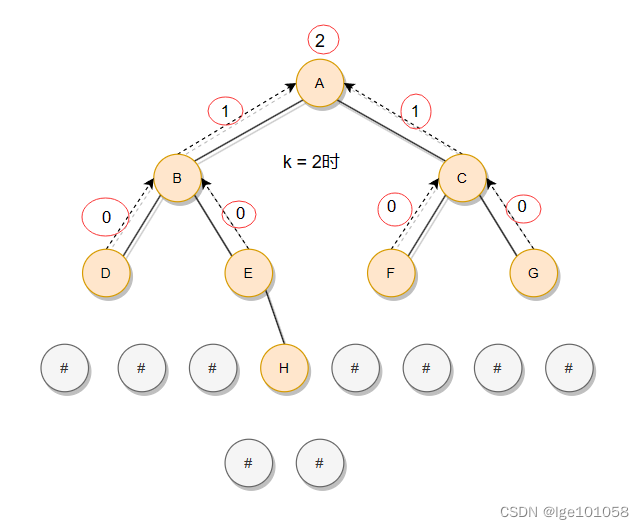
7.二叉树查找值为x的结点

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    // 空结点说明这条路没有找到，返回空
	if (!root)
		return NULL;

    // 如果该结点的值就是待查找的值
	if (root->data == x)
	    // 返回该结点的地址
		return root;

    // 如果没找到
    // 查找左子树
	BTNode* leftnode = BinaryTreeFind(root->left, x);
	// 查找右子树
	BTNode* rightnode = BinaryTreeFind(root->right, x);

    // 如果左子树不为空，说明找到了，返回找到的结点地址
	if (leftnode)
		return leftnode;
	// 如果右子树不为空，说明找到了，返回找到的结点地址
	if (rightnode)
		return rightnode;
	// 都没找到，返回空
	return NULL;
}

??这个查找很简单，前序遍历一边就可以了，找到了就返回找到的结点地址，找不到返回空。

8.二叉树的前序遍历

void BinaryTreePrevOrder(BTNode* root)
{
    // 如果遍历到空结点
	if (!root)
	{
	    // 打印‘#’符号标志一下
		printf("#");
		// 返回
		return;
	}

    // 先打印根结点
	printf("%c", root->data);
	// 再遍历左子树
	BinaryTreePrevOrder(root->left);
	// 最后遍历右子树
	BinaryTreePrevOrder(root->right);
}

9.二叉树的中序遍历

void BinaryTreeInOrder(BTNode* root)
{
    // 如果遍历到空结点
	if (!root)
	{
	    // 打印‘#’符号标志一下
		printf("#");
		// 返回
		return;
	}

    // 遍历左子树
	BinaryTreeInOrder(root->left);
	// 打印根结点
	printf("%c", root->data);
	// 遍历右子树
	BinaryTreeInOrder(root->right);
}

10.二叉树的后序遍历

void BinaryTreePostOrder(BTNode* root)
{
// 如果遍历到空结点
	if (!root)
	{
	    // 打印‘#’符号标志一下
		printf("#");
		// 返回
		return;
	}
    
    // 遍历左子树
	BinaryTreePostOrder(root->left);
	// 遍历右子树
	BinaryTreePostOrder(root->right);
	// 打印根结点
	printf("%c", root->data);
}

??二叉树的遍历都及其相似，只是顺序不同，合理使用递归，根据要求改变函数顺序就可以实现前，中，后序遍历。

七、代码整合及结果演示

1.代码整合

1.头文件 BinaryTree.h 部分

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

// 通过前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);
// 二叉树销毁
void BinaryTreeDestroy(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);

2.源文件 BinaryTree.c 部分

#include"BinaryTree.h"

// 通过前序遍历构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[*pi] == '#')
	{
		++(*pi);
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (!root)
	{
		perror("malloc fail");
		exit(-1);
	}

	root->data = a[(*pi)++];
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);
	return root;
}

// 二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{
	if (!root)
		return;
	
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (!root)
		return 0;
	int leftSize = BinaryTreeLeafSize(root->left);
	int rightSize = BinaryTreeLeafSize(root->right);
	return leftSize + rightSize == 0 ? 1 : leftSize + rightSize;
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (!root || k < 1)
		return 0;
	int leftSize = BinaryTreeLevelKSize(root->left, k - 1);
	int rightSize = BinaryTreeLevelKSize(root->right, k - 1);
	return k == 1 ? leftSize + rightSize + 1 : leftSize + rightSize;
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (!root)
		return NULL;

	if (root->data == x)
		return root;

	BTNode* leftnode = BinaryTreeFind(root->left, x);
	BTNode* rightnode = BinaryTreeFind(root->right, x);

	if (leftnode)
		return leftnode;
	if (rightnode)
		return rightnode;
	return NULL;
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}

	printf("%c", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%c", root->data);
	BinaryTreeInOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c", root->data);
}

3.源文件 test.c 部分

#include"BinaryTree.h"

void test()
{
	char a[] = "ABD##E#H##CF##G##";
	int b = 0;
	BTNode* root = BinaryTreeCreate(a, &b);
	printf("结点个数：%d\n", BinaryTreeSize(root));
	printf("叶子结点个数：%d\n", BinaryTreeLeafSize(root));
	printf("第k层结点个数：%d\n", BinaryTreeLevelKSize(root, 2));
	printf("值为F的结点的地址：%p\n", BinaryTreeFind(root, 'F'));
	printf("二叉树的前序遍历：");
	BinaryTreePrevOrder(root);
	printf("\n");
	printf("二叉树的中序遍历：");
	BinaryTreeInOrder(root);
	printf("\n");
	printf("二叉树的后序遍历：");
	BinaryTreePostOrder(root);
	printf("\n"); 
	BinaryTreeDestroy(root);
	root = NULL;
}

int main()
{
	test();
	return 0;
}

2.结果演示

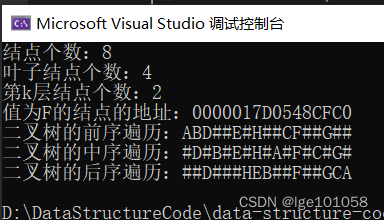
总结

??链式二叉树的实现离不开递归，二叉树的的遍历离不开递归，二叉树的其他函数离不开遍历，所以整个二叉树就像是对递归思想的检验。只要掌握递归的思想，多画画图，对理解二叉树的实现会很有帮助。篇幅较长，难免存在错误，如果发现了错误，还请大家不吝赐教。谢谢。