通信入门系列——采样定理

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录

一、采样保持电路
二、采样周期信号
1、周期矩阵脉冲
2、周期冲激脉冲
三、采样定理
四、频域采样定理

本节内容
一、采样保持电路
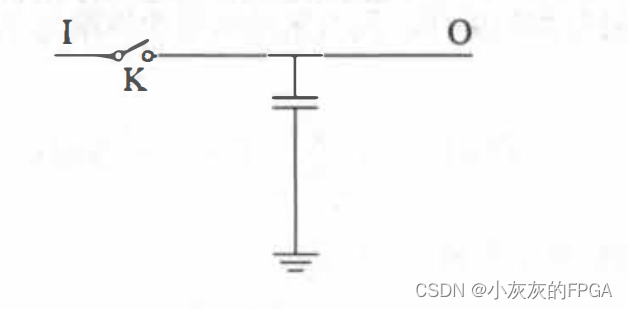
一个基本的采样保持电路，被采样的信号，从I端口输入,从O端口输出,输出后面一般连接A/D转换器，实现模拟信号到数字信号的转换器。开关K闭合的时候为跟随阶段，在此阶段，电容器被充电，电容器两端的电压就是输入信号。开关K端口的时候为保持阶段，在此阶段，电容器上的电压保持不变，A/D转换器开始工作，将所采的样点转换为数字信号。

二、采样周期信号
若输入连续信号x(t)，其傅里叶变换为X(ω),采样，在数学上表示为x(t)与一个采样周期信号p(t)的乘积。通常采样周期信号p(t)为周期矩阵脉冲和周期冲激信号。采样后的信号xs(t)=x(t)p(t)。
采样周期信号p(t),周期为Ts,角速度为ωs=2π/Ts,其傅里叶变换为：

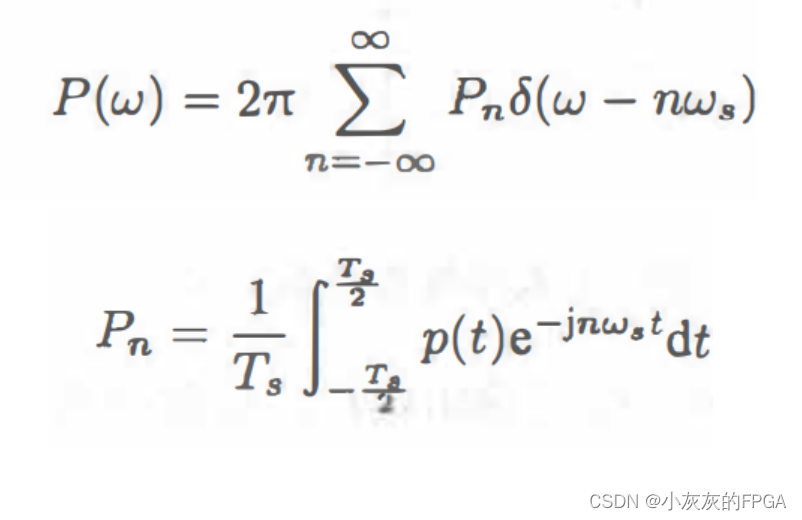
采样后的信号，被采样信号与采样周期信号的乘积，根据卷积定理，其傅里叶变换是两个信号傅里叶变换的卷积，采样后信号的频谱，是连续信号的频谱X(ω)以ωs为周期重复，用采样信号的傅里叶系数加权并且累加得到。即：

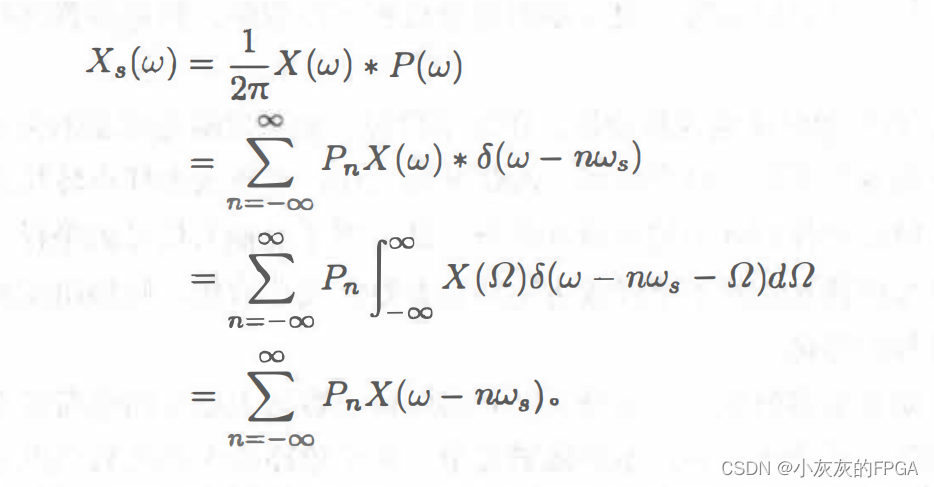
注意：若相邻位置的连续频谱不重叠，相加后互相不影响，那么采样信号的频谱完全保留了原来的连续频谱。
1、周期矩阵脉冲
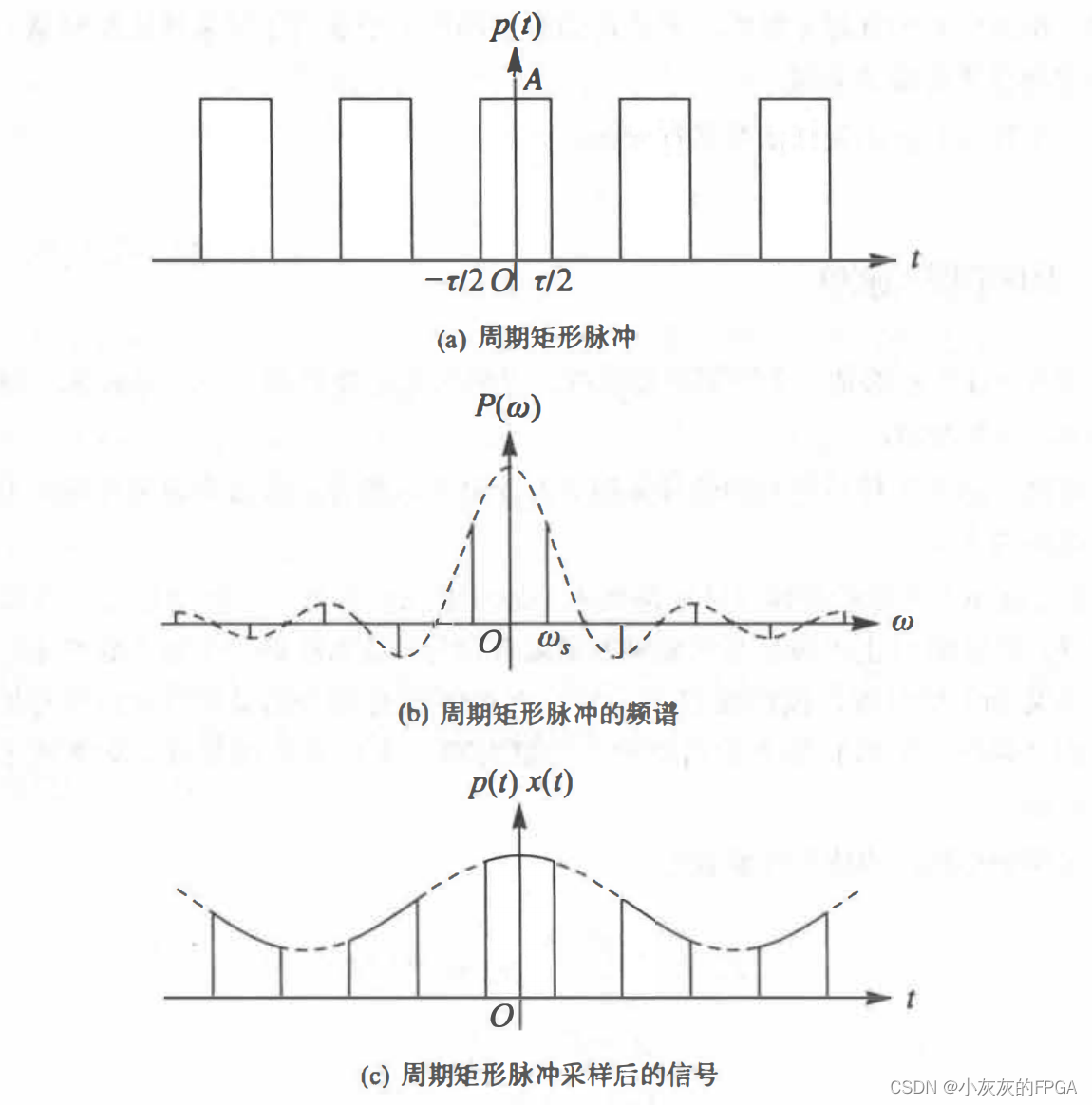
一个周期矩阵脉冲，周期为Ts,角速度为ωs=2π/Ts,脉冲宽度为τ，幅度为A。
周期矩阵脉冲的傅里叶系数为：

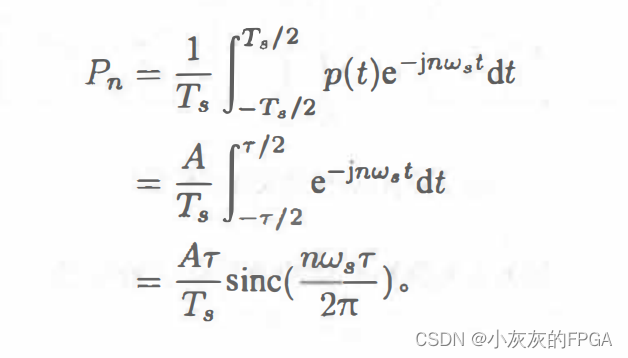
利用周期矩阵脉采样后的信号的傅里叶变换为：

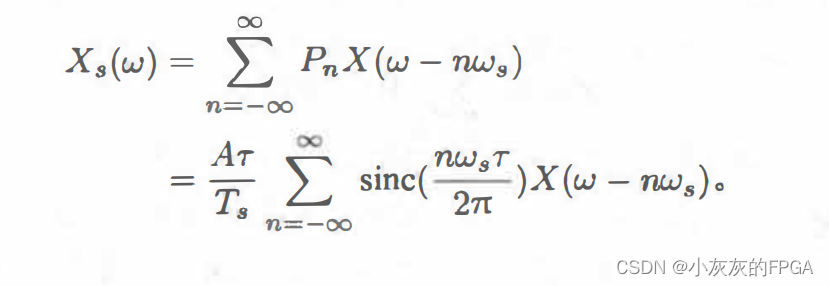
周期矩阵脉冲采样后的频谱，是连续信号的频谱X(ω)以ωs为周期重复，用sinc抽样函数加权并且累加得到。

2、周期冲激脉冲
周期为Ts的周期冲激函数：

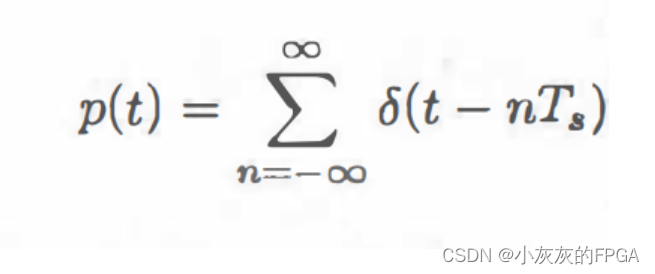
傅里叶系数为：

利用周期冲激脉冲采样后的信号的傅里叶变换为：

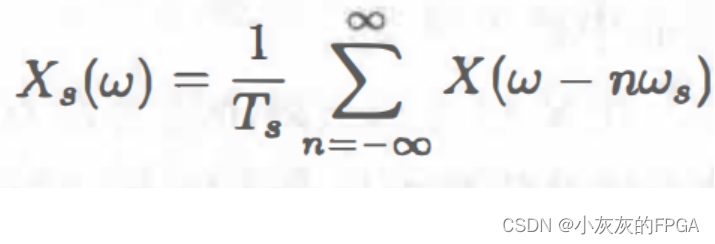
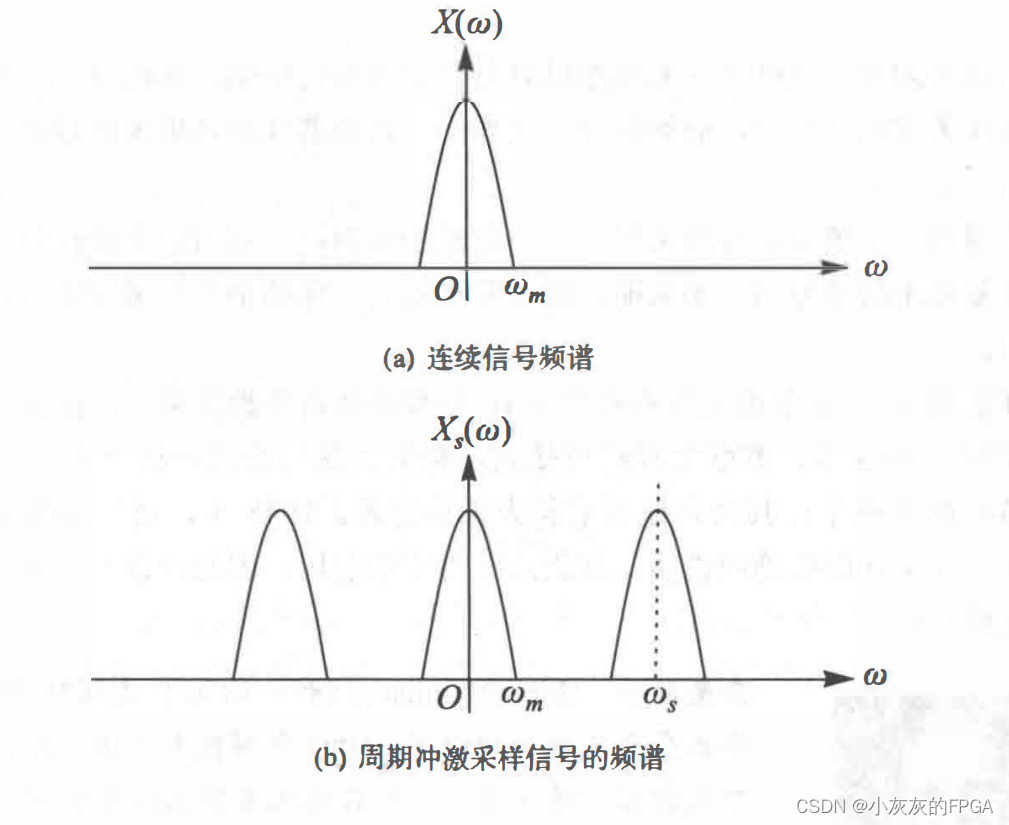
用周期冲激函数采样的信号的频谱，是连续信号的频谱X(ω)以ωs为周期重复并且累加得到。

三、采样定理
1928年，美国物理学家H.奈奎斯特首先提出采样定理，并被称为奈奎斯特采样定理。
采样定理的内容：如果一个带宽有限的信号(即带限信号)的最高角频率为ωm=2πfm，在等间隔采样的条件下，采样频率必须不小于2fm，才能用采样信号无失真地恢复原来的信号，也就是说，采样频率最小为信号最高频率的两倍。
采样信号的频谱是原信号的频谱在nωs的位置重复并且累加的结果。若ωm≤ωs/2,那么相邻的重复频谱可以互相分离而互不影响，通过抽取在零点处的频谱就可以重构原来的信号。若ωm＞ωs/2，那么相邻的重复频谱发送了相互干扰，在信号处理中称为混频现象。混频发送的情况下，无法抽取原来信号的频谱，也无法无失真地重构原来的信号。
四、频域采样定理
如果信号x(t)在时间域内受限，|t|>tm,x(t)=0,那么在频域以不大于1/2tm的频率间隔，对其频谱X(ω)进行采样得到Xs(ω),就可以用Xs(ω)无失真地恢复原信号。