保险箱（寒假每日一题+DP）

题目

小蓝有一个保险箱，保险箱上共有?n?位数字。

小蓝可以任意调整保险箱上的每个数字，每一次操作可以将其中一位增加?1?或减少?1。

当某位原本为?9?或?0?时可能会向前（左边）进位/退位，当最高位（左边第一位）上的数字变化时向前的进位或退位忽略。

例如:

00000 的第?5 位减?1?变为?99999；

99999 的第?5?位减?1?变为?99998；

00000 的第?4?位减?1?变为?99990；

97993 的第?4?位加?1?变为?98003；

99909 的第?3?位加?1?变为?00009。

保险箱上一开始有一个数字?x，小蓝希望把它变成?y，这样才能打开它，问小蓝最少需要操作的次数。

输入格式

输入的第一行包含一个整数?n。

第二行包含一个?n?位整数?x。

第三行包含一个?n?位整数?y。

输出格式

输出一行包含一个整数表示答案。

数据范围

对于?30% 的评测用例，1≤n≤300；
对于?60% 的评测用例，1≤n≤3000；
对于所有评测用例，1≤n≤10^5，x,y 中仅包含数字?0?至?9，可能有前导零。

样例?

输入样例

5
12349
54321

输出样例

11

题目思路

? ? ? ? 我们可以从样例入手，要想将a->b可以对其每个数字进行操作，当每个数字都相等的时候，就达到了目的——a==b；对每个数字进行操作，那么是从左向右遍历，还是从右向左遍历呢？由于我们低位会向高位进位或者借位，这样当我们从左向右进行每个数处理的时候，会被进位所干扰，所以从右向左是解决这道题目的关键。当我们低位已经操作好之后，然后对高位进行操作，无论我们怎么对高位操作是不会影响已经操作好的低位，这样就确保了子问题不会对父问题产生影响，使用dp是较好的选择。以下是有关dp的分析和解题思路。

方法一

?方法二

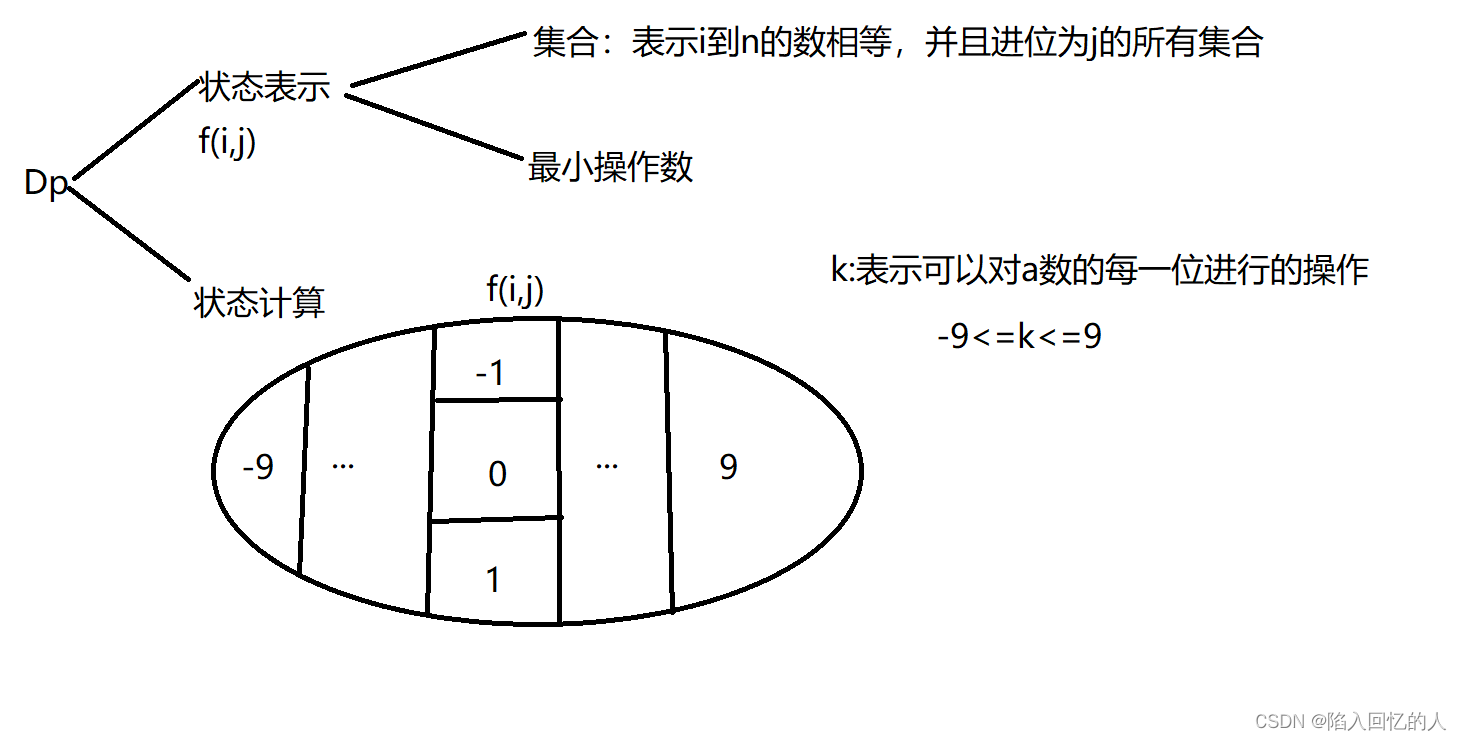
源代码

方法一

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n;
char s1[N], s2[N];
int f[N][3];

int main() {
    cin >> n >> s1 >> s2;
    
    memset(f,0x3f,sizeof f);
    
    f[n][1]=0;
    for(int i=n-1;i>=0;i--){
        int a=s1[i]-'0',b=s2[i]-'0';
        f[i][0]=min({f[i+1][0]+a-1-b+10,f[i+1][1]+a+10-b,f[i+1][2]+a+1+10-b});
        f[i][1]=min({f[i+1][0]+abs(a-1-b),f[i+1][1]+abs(a-b),f[i+1][2]+abs(a+1-b)});
        f[i][2]=min({f[i+1][0]+b+10-(a-1),f[i+1][1]+b+10-a,f[i+1][2]+b+10-(a+1)});
    }
    
    cout << min({f[0][0],f[0][1],f[0][2]}) << endl;
    return 0;
}

方法二

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n;
char s1[N], s2[N];
int f[N][3];

int main() {
    cin >> n >> s1 >> s2;
    
    memset(f,0x3f,sizeof f);
    
    f[n][1]=0;
    for(int i=n-1;i>=0;i--)
        for(int j=0;j<3;j++)
            for(int k=-9;k<=9;k++)
                for(int t=0;t<3;t++)
                    if(s1[i]-s2[i]+k+t-1==(j-1)*10) f[i][j]=min(f[i][j],f[i+1][t]+abs(k));
    
    cout << min({f[0][0],f[0][1],f[0][2]}) << endl;
    return 0;
}