LeetCode day24

LeetCode day24

---

今天主打一个快乐happy(′▽`???)，主要是今天写哈夫曼树被经典文件读取坑麻了（为啥绝对路径能读取，相对不行。罢了）

一个中等题，但是咋感觉很小学捏。。。

2177. 找到和为给定整数的三个连续整数

相关企业

给你一个整数 num ，请你返回三个连续的整数，它们的 和 为 num 。如果 num 无法被表示成三个连续整数的和，请你返回一个 空 数组。

示例 1：

输入：num = 33
输出：[10,11,12]
解释：33 可以表示为 10 + 11 + 12 = 33 。
10, 11, 12 是 3 个连续整数，所以返回 [10, 11, 12] 。

示例 2：

输入：num = 4
输出：[]
解释：没有办法将 4 表示成 3 个连续整数的和。

---

class Solution {
    public long[] sumOfThree(long num) {
        if(num%3!=0){
            return new long[]{};
        }
        else{
            long temp=num/3;
            return new long[]{temp-1,temp,temp+1};
        }
    }
}

嘛，力扣也会跟我们一样的啦。。。

---

LCR 098. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

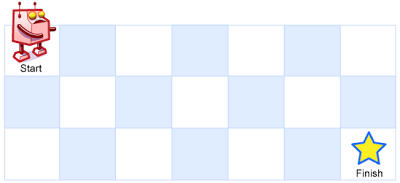
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

---

在草稿上本来想看看是不是有啥规律，巧了，还是得益于前期被dp的打压

class Solution {
    public int uniquePaths(int m, int n) {
        int[][]dp=new int[m+1][n+1];
    
//        dp[1][1]=1;
        for(int row=1;row<=m;row++){
            for(int col=1;col<=n;col++){
              if(row==1&&col==1){
                  dp[row][col]=1;
              }else if(row==1){
                  dp[row][col]=dp[row][col-1];
              }else if(col==1){
                  dp[row][col]=dp[row-1][col];
              }else{
                  dp[row][col]=dp[row-1][col]+dp[row][col-1];
              }
            }
        }
        return dp[m][n];
    }
}

---

LCP 06. 拿硬币

桌上有 n 堆力扣币，每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆，拿走其中的一枚或者两枚，求拿完所有力扣币的最少次数。

示例 1：

输入：[4,2,1]

输出：4

解释：第一堆力扣币最少需要拿 2 次，第二堆最少需要拿 1 次，第三堆最少需要拿 1 次，总共 4 次即可拿完。

示例 2：

输入：[2,3,10]

输出：8

---

额，简单题感觉后面还是来点有意思的写上来，但是今天主打一个快乐happy(′▽`???)

可拿完。

示例 2：

输入：[2,3,10]

输出：8

---

额，简单题感觉后面还是来点有意思的写上来，但是今天主打一个快乐happy(′▽`???)