力扣22. 括号生成（java 回溯法）

Problem: 22. 括号生成

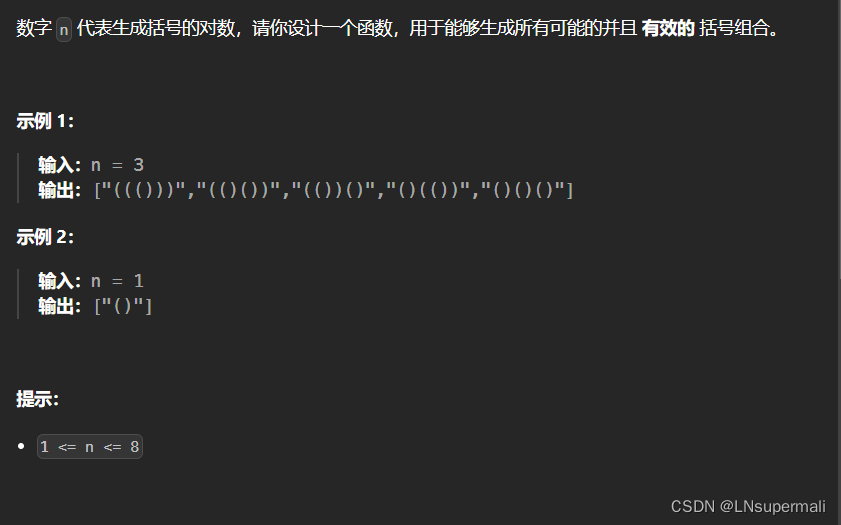
题目描述

思路

我们首先要知道，若想生成正确的括号我们需要让右括号去适配左括号，在此基础上我们利用回溯去解决此题目

1.题目给定n个括号，即当回溯决策路径长度等于$2n$时，我们结束回溯；
2.若想选择出正确的括号，我们先要确定左括号*，即要求左括号小于给定的数量n，同时已经使用的右括号要小于已经使用的左括号，所以我们可以定义已使用的左括号数量lestUsed和已经使用的右括号数量rightUsed,在这两种情况下展开回溯；

解题方法

1.定义结果集合result，决策路劲path（char类型数组，初始化长度为$2n$）；
2.编写并调用回溯函数，初始化决策阶段为0；

2.1当决策路径长度等于$2n$时，将当前的决策路径添加到结果集合中，并返回；
2.2当leftUsed小于n时我们将当前决策路径位置上添上**（，并递归下一阶段（leftUsed 要加一，决策阶段加一）
2.3当rightUsed小于leftUsed时我们将当前决策路径位置上添上），并递归下一阶段（rightUsed 要加一，决策阶段加一）
2.4由于定义的决策路径为一个char类型的数组，所以我们不用显示的恢复当前的决策路径状态**，数组在递归调用中会覆盖上一个

复杂度

时间复杂度:

$O(\frac{1}{n+1}(\genfrac{}{}{0ex}{}{2n}{n}))$

空间复杂度:

$O\left(\frac{4^n}{\sqrt{n}}\right)$

Code

class Solution {
    //Result list
    private List<String> result = new ArrayList<>();

    /**
     * Get all parentheses generated
     *
     * @param n The num of parenthesis
     * @return List<String>
     */
    public List<String> generateParenthesis(int n) {
        //Decision Path
        char[] path = new char[2 * n];
        backtrack(n, 0, 0, 0, path);
        return result;
    }

    /**
     * Use backtracking to get all parentheses generated
     *
     * @param n         The num of parenthesis
     * @param leftUsed  The number of left parentheses used
     * @param rightUsed The number of right parentheses used
     * @param k         Decision stage
     * @param path      Decision path
     */
    private void backtrack(int n, int leftUsed, int rightUsed, int k, char[] path) {
        //End condition
        if (k == 2 * n) {
            result.add(String.valueOf(path));
            return;
        }
        //The leftUsed less than n
        if (leftUsed < n) {
            path[k] = '(';
            backtrack(n, leftUsed + 1, rightUsed, k + 1, path);
        }
        //The rightUsed less than leftUsed
        if (rightUsed < leftUsed) {
            path[k] = ')';
            backtrack(n, leftUsed, rightUsed + 1, k + 1, path);
        }
    }
}