堆的简单实现，堆排序，TopK问题

1.认识堆

意思就是如果是一个大堆的话，根节点不能比所有的子节点小，如果是小堆的话，不能比所有的子节点大。

2. 堆的简单实现

知道什么是堆之后，我们就要对堆精进行一个简单实现：

2.1 堆的向下调整算法

在堆的实现以及应用时，向下调整算法是很重要的，这里给出一个向下调整算法的示例过程：

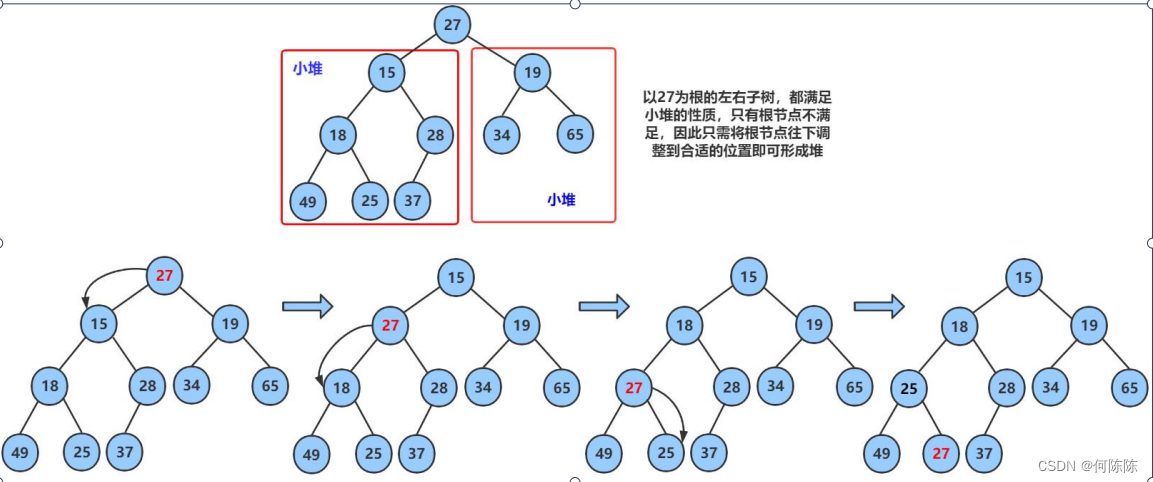
向下调整算法代码如下，这里以建小堆为例：

void swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustDown(HPDataType x, HPDataType* a, HPDataType i)
{
    HPDataType parent
	HPDataType child = 2 * parent + 1;
	while (child < i)
	{
		if (child < i && child + 1 < i && a[child] > a[child + 1])
			child++; 
		if (a[child] < a[parent])  //孩子小于父亲就互相交换
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child = child * 2 + 1;
		}
		else                        //不交换时就退出循环，调整完毕
			break;
	}
}

2.2 堆的创建

2.3 堆的插入：向上调整算法

堆在插入数据的时候，需要使用到向上调整算法，这里先通过图示理解：

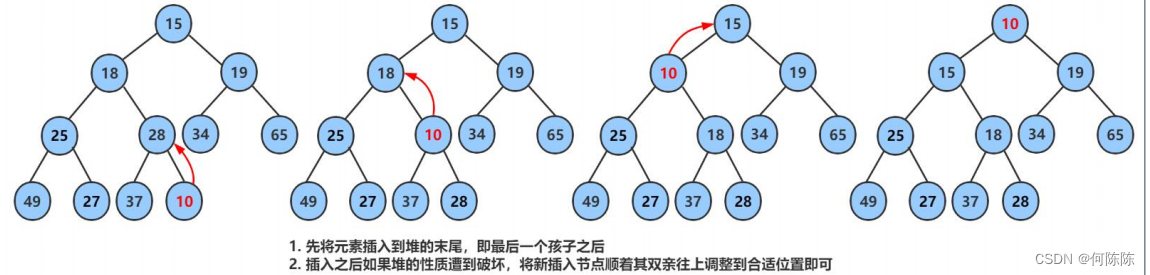
向上调整算法代码如下：

void swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustUp(HPDataType x,HPDataType* a)
{
	HPDataType child = x;
	HPDataType parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
			break;
	}
}

2.4 堆的删除

堆的删除跟顺序表和链表不一样，他不是直接删除最后一个元素

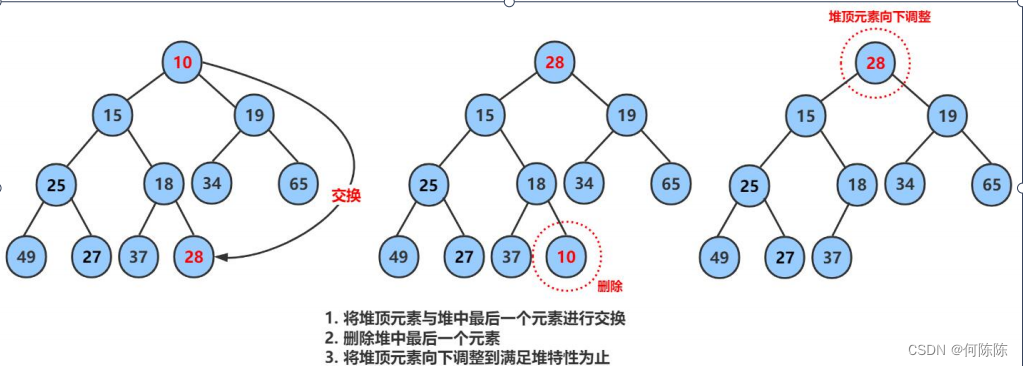
2.5 堆代码的总体实现

下面是堆实现的总体代码：

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
	hp->_size = 0;
	HPDataType* tmp = (HPDataType*)realloc(hp->_a,sizeof(HPDataType)*n);
	if (!tmp)
	{
		perror("realloc fail");
		exit(-1);
	}
	hp->_a = tmp;
	hp->_capacity = n;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
	free(hp->_a);
	hp->_capacity = 0;
	hp->_size = 0;
}
// 堆的插入
void swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustUp(HPDataType x,HPDataType* a)
{
	HPDataType child = x;
	HPDataType parent = (x - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
			break;
	}
}
void HeapPush(Heap* hp, HPDataType x)
{
	if (hp->_size == hp->_capacity)
	{
		HPDataType newcapacity = hp->_capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);
		if (!tmp)
		{
			perror("realloc fail");
			exit(-1);
		}
		hp->_a = tmp;
		hp->_capacity = newcapacity;
	}
	hp->_a[hp->_size] = x;
	hp->_size++;
	AdjustUp(hp->_size-1,hp->_a);
}
void AdjustDown(HPDataType x, HPDataType* a, HPDataType i)
{
	HPDataType child = 2 * x + 1;
	while (child < i)
	{
		if (child < i && child + 1 < i && a[child] > a[child + 1])
			child++;
		if (a[child] < a[x])
		{
			swap(&a[x], &a[child]);
			x = child;
			child = child * 2 + 1;
		}
		else
			break;
	}
}
// 堆的删除
void HeapPop(Heap* hp)
{
	assert(hp);
	swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
	hp->_size--;
	AdjustDown(0, hp->_a,hp->_size);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->_size > 0);
	return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->_size;
}

3. 堆的应用 --- 堆排序

堆排序就是应用堆的思想，对元素进行排序。

代码如下：

void HeapSort(int* a, int n)
{
	// O(N)
	for (int i = (n-1-1)/2; i >= 0; --i)//（n-1-1）/2  是最后一个根节点
	{
		AdjustDown(n, a, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

4. TopK 问题

?2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

注意这里找前k个最大元素是建小堆，因为最小的元素永远在堆顶，新元素如果比堆顶的元素大，他就会与堆顶元素进行交换，交换后进行一轮向下调整算法，堆顶又会出现一个新的最小元素。这样一直循环的与堆顶的元素进行比较替换再向下调整，比堆顶最小的元素还小的元素就不会入堆。最终，堆里面的k个元素就会成为最大的k个元素。同理，如果找最小的几个元素，建大堆也是这个原因。

这里展示一个从1000000个数中找前10个的代码，先造数据到一个文件中，在开始选数，如下：

void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK(int k)
{
	int* arr = (int*)malloc(sizeof(int)*k);
	if (!arr)
	{
		perror("malloc fail");
		exit(-1);
	}
	FILE* fout = fopen("data.txt", "r");
	int j = k;
	int i = 0;
	for(int i=0;i<k;i++)
	{
		fscanf(fout, "%d", &arr[i]);
		AdjustUp(i, arr);
	}
	int x = 0;
	while (fscanf(fout, "%d", &x)!=EOF)   //scanf在完全读取之后,返回EOF,错误输出就返回feof
	{
		if (x > *arr)
		{
			*arr = x;
			AdjustDown(0,arr,k);
		}
	}
	for (int a = 0; a < k; a++)
	{
		printf("%d ", *(arr + a));
	}
	
}