每日一练：LeeCode-144、145、94.二叉树的前中后序遍历【二叉树】

本文是力扣LeeCode-144、145、94.二叉树的前中后序遍历 学习与理解过程，本文仅做学习之用，对本题感兴趣的小伙伴可以出门左拐LeeCode前序遍历、中序遍历、后序遍历。

给你二叉树的根节点 root ，返回它节点值的 前序遍历。

给定一个二叉树的根节点 root ，返回 它的 中序遍历 。

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

题目以前序遍历为例：
示例 1：

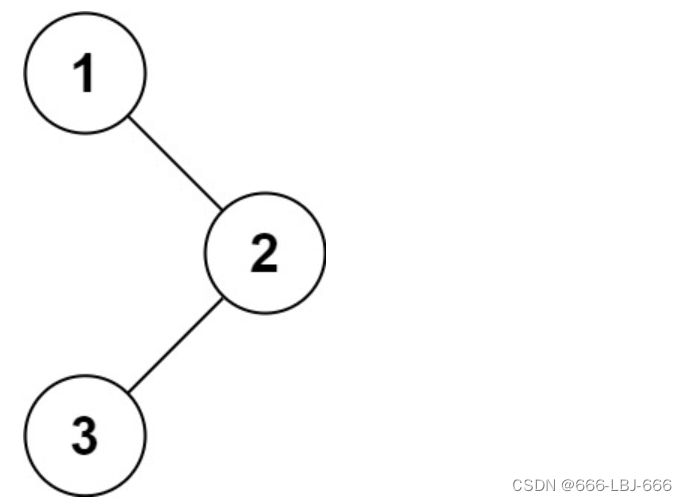
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

示例 5：

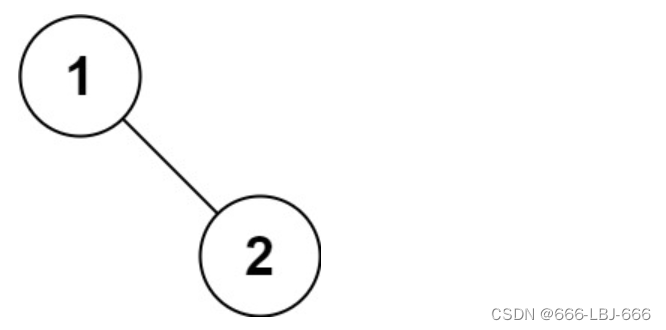
输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

思路

递归法、迭代遍历法

1、递归法

1）确定递归函数的参数和返回值
2）确定终?条件
3）确定单层递归的逻辑

代码实现

前序遍历（中左右）：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        
        List<Integer> res = new ArrayList<>();
        preOrder(root,res);
        return res;
    }

    public void preOrder(TreeNode root,List<Integer> res){	//确定递归函数的参数和返回值
        if(root==null)return;	//确定终?条件
		//确定单层递归的逻辑
        res.add(root.val);
        preOrder(root.left,res);
        preOrder(root.right,res);
    }
}

中序遍历（左中右）：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        
        List<Integer> res = new ArrayList<>();
        preOrder(root,res);
        return res;
    }

    public void preOrder(TreeNode root,List<Integer> res){	//确定递归函数的参数和返回值
        if(root==null)return;	//确定终?条件
		//确定单层递归的逻辑
        preOrder(root.left,res);
        res.add(root.val);
        preOrder(root.right,res);
    }
}

后序遍历（左右中）:

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        
        List<Integer> res = new ArrayList<>();
        preOrder(root,res);
        return res;
    }

    public void preOrder(TreeNode root,List<Integer> res){	//确定递归函数的参数和返回值
        if(root==null)return;	//确定终?条件
		//确定单层递归的逻辑
        preOrder(root.left,res);
        preOrder(root.right,res);
        res.add(root.val);
    }
}

2、迭代遍历法

递归其实也是使用栈这种数据结构，只是不是显式地调用，迭代遍历法，就是用到栈实现
前序遍历（中左右）：
由于栈的特性，我们需要先将根节点入栈，遍历完后，然后将右孩子入栈，再将左孩子入栈,因为这样才能保证遍历顺序是中左右

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> res = new ArrayList<>();
        if(root == null)return res;
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();	// 中
            res.add(node.val);
            if(node.right!=null)stack.push(node.right);	// 右（空节点不?栈）
            if(node.left!=null)stack.push(node.left);	// 左（空节点不?栈）
        }
        return res;
    }
}

前序遍历的迭代遍历后，可以轻易带出后序遍历
后序遍历（左右中）：
后序遍历的遍历顺序为：左右中，前序遍历为中左右，可以先将根节点入栈，遍历完后，然后将右左孩子入栈，再将右孩子入栈，最后将结果反转数组即可。

代码实现

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> res = new ArrayList<>();
        if(root == null)return res;
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            res.add(node.val);
            if(node.left!=null)stack.push(node.left);	//先将左孩子入栈
            if(node.right!=null)stack.push(node.right);	//再将右孩子入栈，以保证反转后的顺序
        }
        Collections.reverse(res);	//结果反转
        return res;
    }
}

中序遍历（左中右）：

由于中序遍历的遍历访问顺序（从根节点到叶子结点，从上往下） 和 左中右的处理顺序不一样，前序和后序是一致的，所以，我们需要先使用指针，从最左边的叶子结点开始处理，利用栈的出栈顺序，一个一个往根节点上走，然后处理到根节点后，再处理根节点的右孩子

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new  Stack<>();
        List<Integer> res = new ArrayList<>();
        TreeNode cur = root;
        while(cur!=null || !stack.isEmpty()){
            if(cur!=null){	 // 指针来访问节点，访问到最底层
                stack.push(cur);	// 将访问的节点放进栈
                cur = cur.left;		// 左
            }else{
                cur = stack.pop();	 // 从栈?弹出的数据，就是要处理的数据（放进result数组?的数据）
                res.add(cur.val);	// 中
                cur = cur.right;	// 右
            }
        }
        return res;
    }
}

最重要的一句话：做二叉树的题目，首先需要确认的是遍历顺序
大佬们有更好的方法，请不吝赐教，谢谢