平衡二叉树(AVL)的插入(C++)
发布时间:2024年01月17日
平衡二叉树
一颗AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(平衡因子)的绝对值不超过1
如果一颗二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2n),搜索时间复杂度O(log2n)。
如图:该树就是一个平衡二叉树
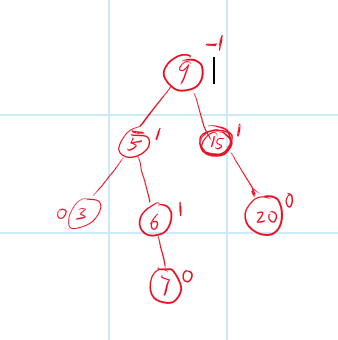
AVL树结点定义
我们使用带有parent的结点来定义AVL结点,这样方便我们找一个结点的父节点。并且数据是一个键值对。
实现如下:
//std命名空间要展开,否则pair没法用
template<class K, class V>
struct AVLTreeNode
{
struct AVLTreeNode<K, V>* _left;
struct AVLTreeNode<K, V>* _right;
struct AVLTreeNode<K, V>* _parent; //指向父节点
pair<K, V> _kv; //数据
int _bf; //平衡因子
//构造函数
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
};
AVL树的插入
插入
AVL树的插入和二叉搜索树一样,遵循根大于左子树,小于右子树的规则。插入部分如下:
template<class K, class V>
class AVLTree
{
private:
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
//根为空, 直接创建
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
//1.先找到结点,然后插入
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right; // 向右走
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left; //向左走
}
else //相等
{
return false;
}
}
//找到了,插入
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
}
只需记住维护的是带parent的节点,记得双向链接即可。
更新平衡因子
由于平衡因子的存在,插入完成后要调节平衡因子。
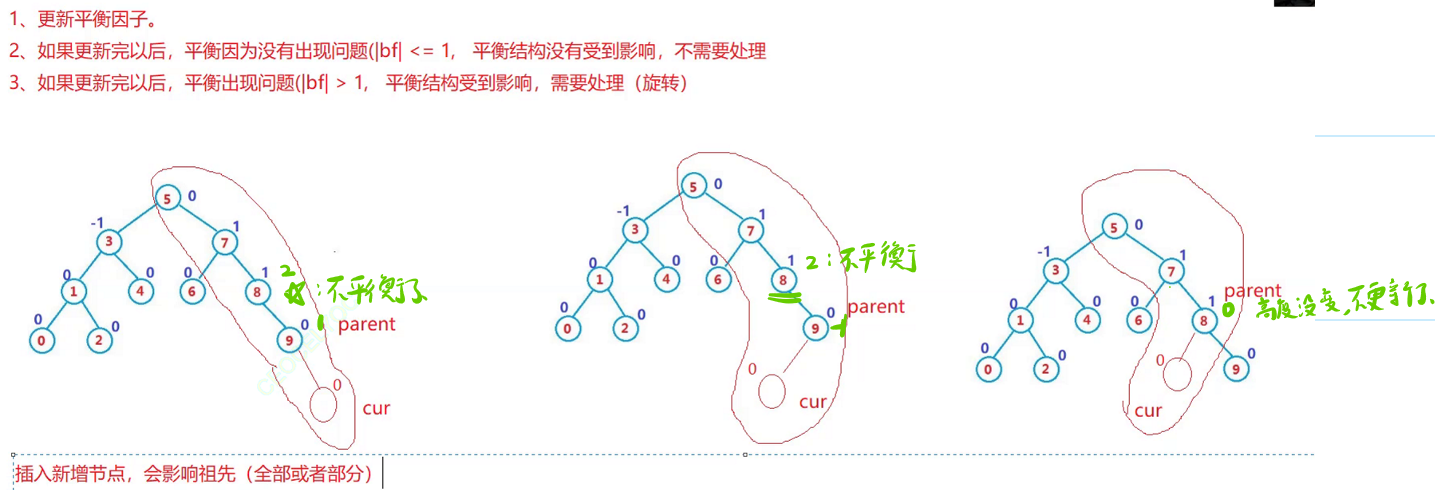
观察上图可知,红色的结点插入之后,有结点相应的平衡因子变成了2,平衡受到影响需要旋转;而有的平衡因子没有变成2,因此不需要旋转了。
那么需要怎么调节平衡因子呢?通过分析我们可以知道:
- 在parent结点的左孩子插入,平衡因子-1
- 在parent的右孩子插入,平衡因子+1
什么时候决定是否要网上更新爷爷结点呢?取决于parent所在的子树高度是否发生变化,高度变了继续更新,不变不更新。
- 插入后parent->bf ==1 || parent->bf == -1,就更新。说明插入之前parent->bf == 0(不可能是2或者-2,否则插入之前就不是AVL树了),左右两边高度相等,插入一个节点后,其中一边就变高了。说明parent的子树高度变了。
- parent -> bf ==2 || parent -> bf ==-2。说明parent所在的子树不平衡需要处理。
- parent-> bf == 0 。 说明parent所在的子树高度不变,不用继续往上更新(说明插入前是1或者-1,是一边高一边低,插入后把低的这边补上了)。
代码如下:
template<class K, class V>
class AVLTree
{
private:
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
//插入逻辑省略
//调整平衡因子:平衡因子是右子树高度-左子树高度
//如果|bf|<=1,说明插入成功,否则需要旋转
while (parent)
{
//1.当在左边插入,parent--, 在右边插入,parent++
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//2.父节点bf调节后,等于0,说明恰好平衡(不影响本身高度),不再调爷爷的bf
//父节点bf=1/-1,说明是从bf=0过来的。不可能为2或者-2(否则不满足AVL树的平衡要求),改变了子树的高度,因此,还要继续向上调节。(重复过程,直至为根)
//父节点bf=2/-2,停止调节,说明此时发生了不平衡。(要旋转了!)
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) //接着向上调节
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//旋转
}
else
{
assert(false); //哪种情况都不是,说明程序有误
}
}
return true;
}
旋转
旋转有四种情况,分别是
- 右单旋:新节点插入到较高左子树的左侧
- 左单旋:新节点插入到较高右子树的右侧
- 左右双旋:新节点插入到较高左子树的右侧
- 右左双旋:新节点插入到较高右子树的左侧
右单旋
新节点插入到较高左子树的左侧,如下图所示:
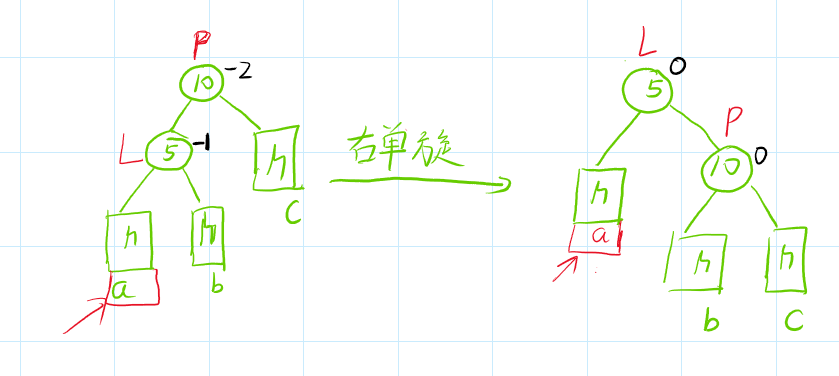
由图可知,右单旋把本来不平衡的树,变为平衡了。
代码如下:
void _RotateR(Node* parent)
{
//右单旋,儿子上位变父亲,父亲被挤到右边
Node* pParent = parent->_parent; //爷爷
Node* childL = parent->_left; //左孩子
parent->_left = childL->_right;
if (childL->_right) //如果孩子的左为空,就不访问
{
childL->_right->_parent = parent; //子指向父
}
childL->_right = parent;
parent->_parent = childL; //子指向父
//最后将chldL指向pParent
childL->_parent = pParent;
if (pParent == nullptr) // childL 变成了根
{
_root = childL;
childL->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = childL;
}
else
{
pParent->_right = childL;
}
}
//最后更新parent 和 childL的平衡因子
childL->_bf = parent->_bf = 0;
}
左单旋
新节点插入到较高右子树的右侧,如下图所示:
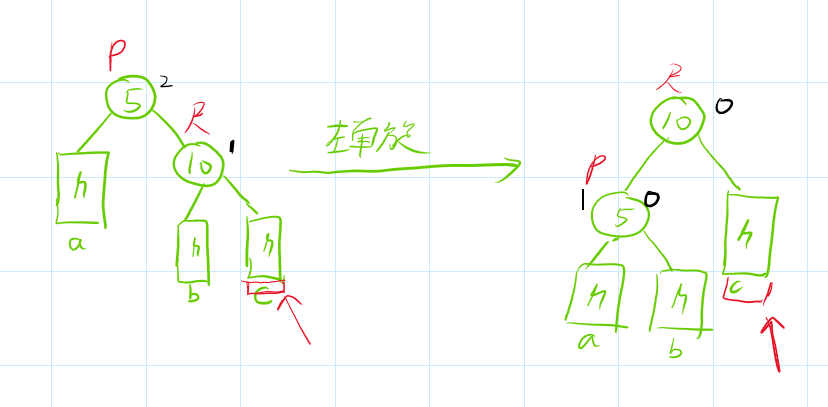
由图可知,左单旋把本来不平衡的树,变为平衡了。
//左单旋
void _RotateL(Node* parent)
{
Node* childR = parent->_right; //存右孩子
parent->_right = childR->_left; //右孩子的左孩子互连父亲
if (childR->_left)
{
childR->_left->_parent = parent;
}
childR->_left = parent; //parent和childR互联
Node* pparent = parent->_parent; //暂存爷爷
parent->_parent = childR;
//爷爷和childR互联
childR->_parent = pparent;
if (pparent == nullptr) //爷爷为空,就是根
{
_root = childR;
childR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = childR;
}
else
{
pparent->_right = childR;
}
}
//连完调整平衡因子
childR->_bf = parent->_bf = 0;
}
左右双旋
新节点插入到较高左子树的右侧,如图所示:下图是插入的所有情况,区别只是,最终的平衡因子有所不同。
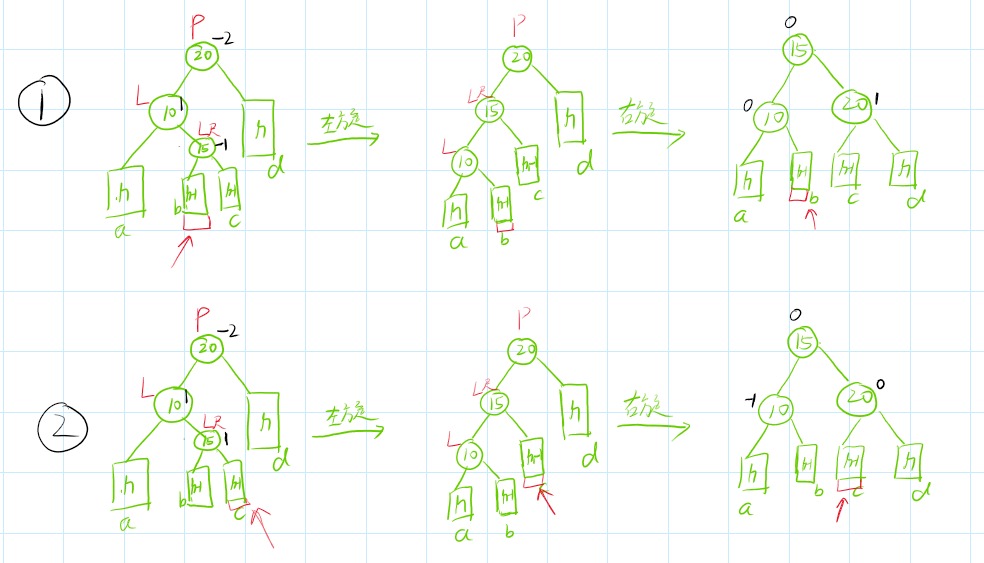
还有一种特殊情况,没有被包括在上面,就是当ad子树为空时,那么bc必为空。此时也会产生不平衡,如下图所示:
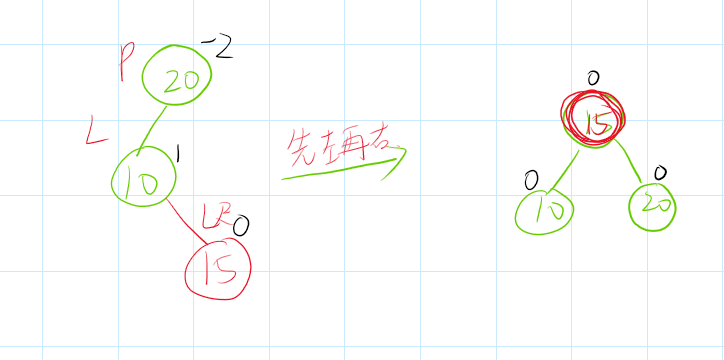
此时的平衡因此全为空,因此要特殊处理一下:
void _RotateLR(Node* parent)
{
Node* childL = parent->_left;
Node* childLR = childL->_right;
//暂存childRL的bf,因为旋转会清空,不然的话特殊情况会出问题。
int bf = childLR->_bf;
_RotateL(parent->_left);
_RotateR(parent);
//if (childLR->_bf == -1)
if (bf == -1)
{
parent->_bf = 1;
childL->_bf = 0;
childLR->_bf = 0;
}
//else if (childLR->_bf == 1)
else if (bf == 1)
{
parent->_bf = 0;
childL->_bf = -1;
childLR->_bf = 0;
}
//else if (childLR->_bf == 0)
else if (bf == 0)
{
parent->_bf = 0;
childL->_bf = 0;
childLR->_bf = 0;
}
else
{
assert(false);
}
}
右左双旋
该情况和左右双旋相反,请读者自行推导:
void _RotateRL(Node* parent)
{
Node* childR = parent->_right;
Node* childRL = childR->_left;
//暂存childRL的bf,因为旋转会清空
int bf = childRL->_bf;
_RotateR(parent->_right);
_RotateL(parent);
//if (childRL->_bf == 1)
if (bf == 1)
{
parent->_bf = -1;
childR->_bf = 0;
childRL->_bf = 0;
}
else if (bf == -1)
//else if (childRL->_bf == -1)
{
parent->_bf = 0;
childR->_bf = 1;
childRL->_bf = 0;
}
//else if (childRL->_bf == 0)
else if (bf == 0)
{
parent->_bf = 0;
childR->_bf = 0;
childRL->_bf = 0;
}
else
{
assert(false);
}
}
完整插入代码如下:
namespace xty
{
template<class K, class V>
struct AVLTreeNode
{
struct AVLTreeNode<K, V>* _left;
struct AVLTreeNode<K, V>* _right;
struct AVLTreeNode<K, V>* _parent; //指向父节点
pair<K, V> _kv;
int _bf;
//构造函数
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
};
template<class K, class V>
class AVLTree
{
private:
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
//根为空, 直接创建
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
//1.先找到结点,然后插入
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right; // 向右走
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left; //向左走
}
else //相等
{
return false;
}
}
//找到了,插入
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//调整平衡因子:平衡因子是右子树高度-左子树高度
//如果|bf|<=1,说明插入成功,否则需要旋转
while (parent)
{
//1.当在左边插入,parent--, 在右边插入,parent++
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//2.父节点bf调节后,等于0,说明恰好平衡(不影响本身高度),不再调爷爷的bf
//父节点bf=1/-1,说明是从bf=0过来的。不可能为2或者-2(否则不满足AVL树的平衡要求),改变了子树的高度,因此,还要继续向上调节。(重复过程,直至为根)
//父节点bf=2/-2,停止调节,说明此时发生了不平衡。(要旋转了!)
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) //接着向上调节
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//需要旋转
if (parent->_bf == -2 && parent->_left->_bf == -1) //右单旋
{
_RotateR(parent);
}
else if (parent->_bf == 2 && parent->_right->_bf == 1) //左单旋
{
_RotateL(parent);
}
else if (parent->_bf == -2 && parent->_left->_bf == 1) //LR旋转
{
_RotateLR(parent);
}
else if (parent->_bf == 2 && parent->_right->_bf == -1) //RL旋转
{
_RotateRL(parent);
}
else
{
assert(false);
}
//旋转完成,就意味着插入彻底结束了
break;
}
else
{
assert(false); //哪种情况都不是,说明程序有误
}
}
return true;
}
private:
void _RotateR(Node* parent)
{
//右单旋,儿子上位变父亲,父亲被挤到右边
Node* pParent = parent->_parent; //爷爷
Node* childL = parent->_left; //左孩子
parent->_left = childL->_right;
if (childL->_right)
{
childL->_right->_parent = parent; //子指向父
}
childL->_right = parent;
parent->_parent = childL; //子指向父
//最后将chldL指向pParent
childL->_parent = pParent;
if (pParent == nullptr) // childL 变成了根
{
_root = childL;
childL->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = childL;
}
else
{
pParent->_right = childL;
}
}
//最后更新parent 和 childL的平衡因子
childL->_bf = parent->_bf = 0;
}
//左单旋
void _RotateL(Node* parent)
{
Node* childR = parent->_right; //存右孩子
parent->_right = childR->_left; //右孩子的左孩子互连父亲
if (childR->_left)
{
childR->_left->_parent = parent;
}
childR->_left = parent; //parent和childR互联
Node* pparent = parent->_parent; //暂存爷爷
parent->_parent = childR;
//爷爷和childR互联
childR->_parent = pparent;
if (pparent == nullptr) //爷爷为空,就是根
{
_root = childR;
childR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = childR;
}
else
{
pparent->_right = childR;
}
}
//连完调整平衡因子
childR->_bf = parent->_bf = 0;
}
void _RotateLR(Node* parent)
{
Node* childL = parent->_left;
Node* childLR = childL->_right;
//暂存childRL的bf,因为旋转会清空
int bf = childLR->_bf;
_RotateL(parent->_left);
_RotateR(parent);
//if (childLR->_bf == -1)
if (bf == -1)
{
parent->_bf = 1;
childL->_bf = 0;
childLR->_bf = 0;
}
//else if (childLR->_bf == 1)
else if (bf == 1)
{
parent->_bf = 0;
childL->_bf = -1;
childLR->_bf = 0;
}
//else if (childLR->_bf == 0)
else if (bf == 0)
{
parent->_bf = 0;
childL->_bf = 0;
childLR->_bf = 0;
}
else
{
assert(false);
}
}
void _RotateRL(Node* parent)
{
Node* childR = parent->_right;
Node* childRL = childR->_left;
//暂存childRL的bf,因为旋转会清空
int bf = childRL->_bf;
_RotateR(parent->_right);
_RotateL(parent);
//if (childRL->_bf == 1)
if (bf == 1)
{
parent->_bf = -1;
childR->_bf = 0;
childRL->_bf = 0;
}
else if (bf == -1)
//else if (childRL->_bf == -1)
{
parent->_bf = 0;
childR->_bf = 1;
childRL->_bf = 0;
}
//else if (childRL->_bf == 0)
else if (bf == 0)
{
parent->_bf = 0;
childR->_bf = 0;
childRL->_bf = 0;
}
else
{
assert(false);
}
}
private:
Node* _root = nullptr;
};
测试代码写的对不对
- 首先要中序遍历,检查二叉树是不是符合升序。
- 检查平衡因子的绝对值是否>=2。
- 检查每个结点的左右子树高度差,是否和平衡因子相等。
使用下面代码检查:
void InOrder()
{
_InOrder(_root);
}
bool IsBalanceTree()
{
return _IsBalanceTree(_root);
}
bool _IsBalanceTree(Node* root)
{
//1.中序遍历为有序数
//2.验证每个子树的高度差的绝对值不超过1
//3.验证结点平衡因子是否计算正确
if (root == nullptr)
{
return true;
}
int left = _Height(root->_left);
int right = _Height(root->_right);
int bf = root->_bf;
if (right - left != bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
if (abs(right - left) >= 2)
{
cout << root->_kv.first << "树高异常" << endl;
return false;
}
return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
int _Height(Node* root) //计算子树的高度 非树的高度!!!!!!!!
{
if (root == nullptr)
{
return 0;
}
int left = _Height(root->_left);
int right = _Height(root->_right);
return left > right ? left + 1 : right + 1;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
测试函数:
void AVLTest1()
{
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int, int> t;
for (auto e : a)
{
t.Insert(pair<int, int>(e, 0));
t.InOrder();
cout << endl;
}
t.InOrder();
}
void AVLTest2()
{
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int, int> t;
for (auto e : a)
{
if (e == 14)
{
int x = 0;
}
cout << e << endl;
t.Insert(pair<int, int>(e, 0));
cout << t.IsBalanceTree() << endl;
}
t.InOrder();
cout << t.IsBalanceTree() << endl;
}
}
文章来源:https://blog.csdn.net/weixin_45153969/article/details/135616082
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JavaWeb笔记之前端开发JQuery
- c语言考试代码
- 机器人跟踪性能量化指标
- 【稳定检索|投稿优惠】2024年绿色能源与电网电力系统国际会议(ICGEGPS 2024)
- 如何在Go中使用日期和时间
- Vue 3 hooks的基本使用及疑问
- QMainWindows_状态栏_铆接部件_中心部件
- Cypress FX2LP No EEPROM Device逻辑分析仪固件修复
- 2023年【G2电站锅炉司炉】考试题库及G2电站锅炉司炉考试报名
- 为什么要选择“零代码”开发的智慧能源管理平台?