强网杯2023 crypto

speed up

当时看到这个题目 也是觉得易懂 并且可以解出来的

但是数字实在是过大了兄弟

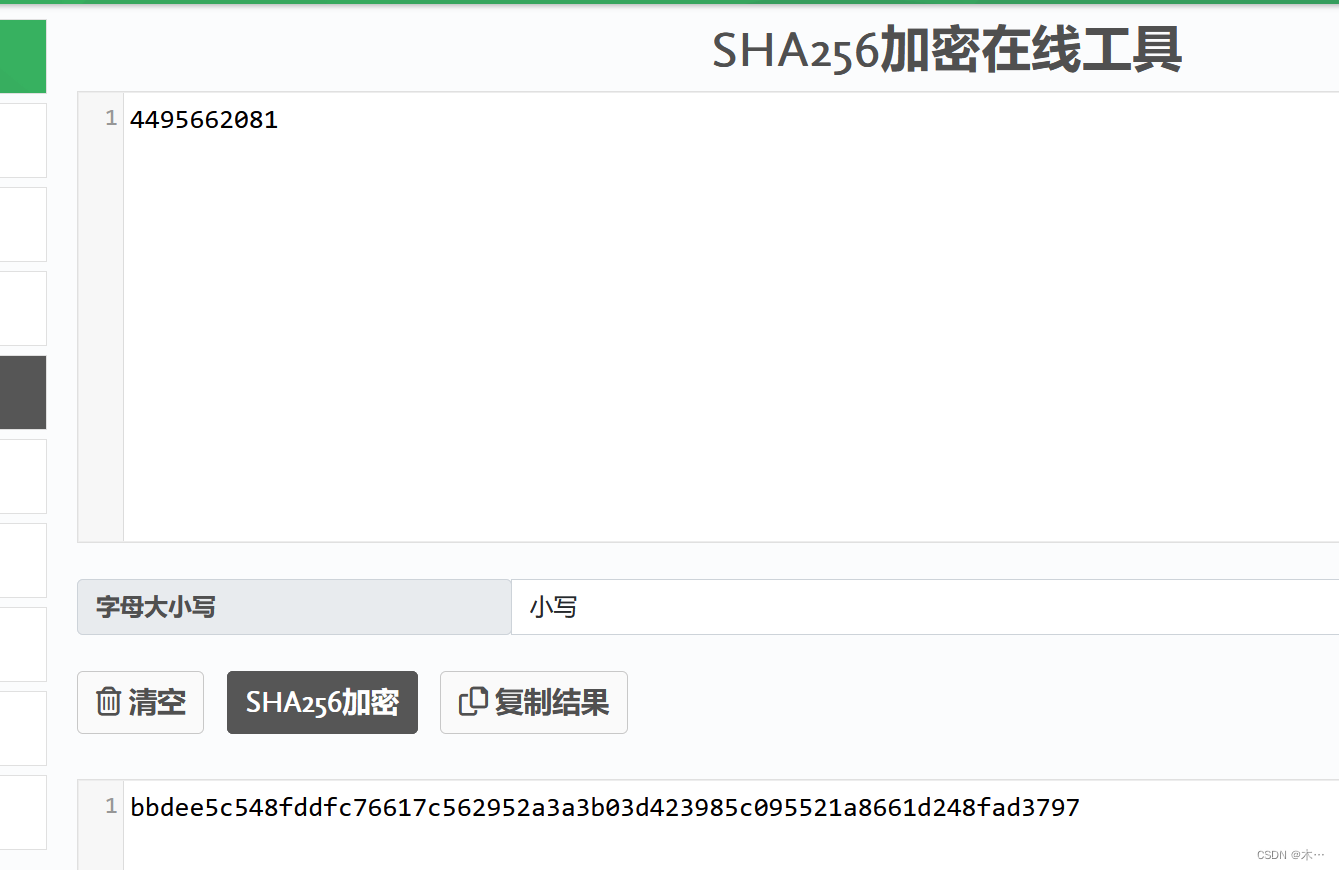
题目意思是计算2^27的阶乘,并获取得到每一位数的数字之和,flag即为该数字的sha256编码?

2^27为134217728

gmpy2包是支持大数运算的,故利用其fac方法进行尝试,在等待一段时间后可以得到对应的结果

参考了其他师傅的wp

import gmpy2

number = 134217728 # 要计算阶乘的数字

result = gmpy2.fac(number)
digit_sum = 0
for digit_char in str(result):
  digit_sum += int(digit_char)

print(f"{number}阶乘的各位数字之和为{digit_sum}")

得到运行结果为:4495662081

然后利用一个在线工具进行sha256加密即可得到flag

not only rsa?

out.txt

n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943

?task.py

from Crypto.Util.number import bytes_to_long
from secret import flag
import os

n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
m = bytes_to_long(flag)

flag = flag + os.urandom(n.bit_length() // 8 - len(flag) - 1)
m = bytes_to_long(flag)

c = pow(m, e, n)

with open('out.txt', 'w') as f:
    print(f"{n = }", file=f)
    print(f"{e = }", file=f)
    print(f"{c = }", file=f)

拿到这么大的n 肯定先拿factordb.com分解一下看看

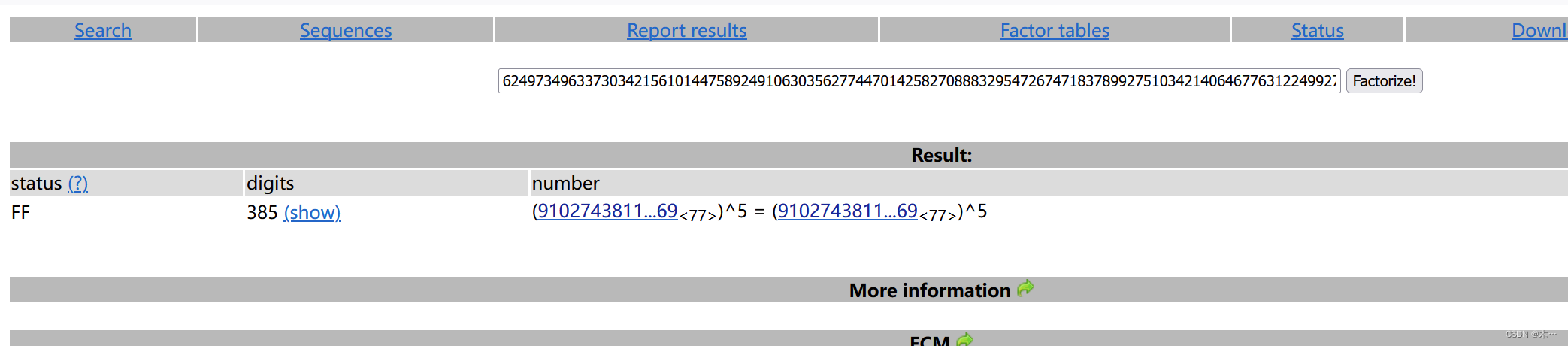发现n不能由两个大数分解得到，而是91027438112295439314606669837102361953591324472804851543344131406676387779969的5次方

n=p5
?(n)=p4(p?1)?(n)=p4(p?1)?? ----》欧拉函数
ed≡1(mod?p4(p?1))ed≡1(mod?p4(p?1))
e和?(n)?(n)不互质，考虑AMM
c≡me(mod?n)c≡me(mod?n)
同余性质转到：
c≡me(mod?p)c≡me(mod?p)
用AMM得到：
mp≡m(mod?p)mp?≡m(mod?p)
考虑用Hensel将模p下结果提升到p5

AMM算法参考宸极实验室—『CTF』AMM 算法详解与应用 - 知乎

尝试用nth_roots直接开到p5

这里利用sagemath数学工具的求模方程源根的函数进行尝试暴力求解

第一次使用

不大会

参考

https://www.cnblogs.com/Nuy0ah/p/17158895.html#:~:text=%E5%AE%98%E7%BD%91%E9%93%BE%E6%8E%A5%EF%BC%9Ahttps%3A%2F%2Fwww.sagemath.org%2Fdownload.html%20%E9%80%89%E6%8B%A9%E7%A6%BB%E8%87%AA%E5%B7%B1%E6%9C%80%E8%BF%91%E7%9A%84%E6%9C%8D%E5%8A%A1%E5%99%A8%E5%9C%B0%E5%9D%80%20%E9%80%89%E6%8B%A9%E6%B8%85%E5%8D%8E%E7%9A%84%E6%9C%8D%E5%8A%A1%E5%99%A8%20%E5%AE%89%E8%A3%85%E5%9C%A8%E6%9C%AC%E5%9C%B0%E6%89%80%E4%BB%A5%E7%9B%B4%E6%8E%A5%E9%80%89%E6%8B%A9windows%E7%89%88%E6%9C%AC,%E4%B8%8B%E8%BD%BD%E5%AE%8C%E6%88%90%E5%90%8E%E5%8F%8C%E5%87%BB%E5%BC%80%E5%A7%8B%E5%AE%89%E8%A3%85%20%E5%AE%89%E8%A3%85%E8%BF%87%E7%A8%8B%E4%B8%AD%E6%9B%B4%E6%94%B9%E5%B7%A5%E4%BD%9C%E7%9B%AE%E5%BD%95%E7%84%B6%E5%90%8E%E4%B8%80%E8%B7%AFnext%E7%AD%89%E5%BE%85%E5%AE%89%E8%A3%85%E5%8D%B3%E5%8F%AF%20%21%20%5Bimage%5D%20%28https%3A%2F%2Fimg202

这里还要安装第三方库

在shell里面执行（这个就好像终端 命令也都差不多）

pip install pycryptodome

我在目录下创建了一个hello.sage

先测试一下：

print (“hello world”)

# SageMath
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
# factordb: n = p^5
p = 91027438112295439314606669837102361953591324472804851543344131406676387779969
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943

pari(f"addprimes({p})")
rs = mod(c, p^5).nth_root(e, all=True)
from Crypto.Util.number import *
for r in rs:
    flag = long_to_bytes(int(r))
    if b'flag' in flag:
        print(flag)

discrete_log?

task.py

from Crypto.Util.number import *
from Crypto.Util.Padding import pad
flag = 'flag{d3b07b0d416ebb}'

assert len(flag) <= 45
assert flag.startswith('flag{')
assert flag.endswith('}')

m = bytes_to_long(pad(flag.encode(), 128))

p = 0xf6e82946a9e7657cebcd14018a314a33c48b80552169f3069923d49c301f8dbfc6a1ca82902fc99a9e8aff92cef927e8695baeba694ad79b309af3b6a190514cb6bfa98bbda651f9dc8f80d8490a47e8b7b22ba32dd5f24fd7ee058b4f6659726b9ac50c8a7f97c3c4a48f830bc2767a15c16fe28a9b9f4ca3949ab6eb2e53c3
g = 5

assert m < (p - 1)

c = pow(g, m, p)

with open('out.txt', 'w') as f:
    print(f"{p = }", file=f)
    print(f"{g = }", file=f)
    print(f"{c = }", file=f)

?out.txt

p = 173383907346370188246634353442514171630882212643019826706575120637048836061602034776136960080336351252616860522273644431927909101923807914940397420063587913080793842100264484222211278105783220210128152062330954876427406484701993115395306434064667136148361558851998019806319799444970703714594938822660931343299
g = 5
c = 105956730578629949992232286714779776923846577007389446302378719229216496867835280661431342821159505656015790792811649783966417989318584221840008436316642333656736724414761508478750342102083967959048112859470526771487533503436337125728018422740023680376681927932966058904269005466550073181194896860353202252854

看不懂 就是相遇思想

?

import itertools

from gmpy2 import *

from Crypto.Util.Padding import *

from Crypto.Util.number import *

from tqdm import tqdm



p = 173383907346370188246634353442514171630882212643019826706575120637048836061602034776136960080336351252616860522273644431927909101923807914940397420063587913080793842100264484222211278105783220210128152062330954876427406484701993115395306434064667136148361558851998019806319799444970703714594938822660931343299

g = 5

c = 105956730578629949992232286714779776923846577007389446302378719229216496867835280661431342821159505656015790792811649783966417989318584221840008436316642333656736724414761508478750342102083967959048112859470526771487533503436337125728018422740023680376681927932966058904269005466550073181194896860353202252854

q = 86691953673185094123317176721257085815441106321509913353287560318524418030801017388068480040168175626308430261136822215963954550961903957470198710031793956540396921050132242111105639052891610105064076031165477438213703242350996557697653217032333568074180779425999009903159899722485351857297469411330465671649



flag_len=12

fake_flag_pad='flag{'.encode() +'\x00'.encode()*flag_len+'}'.encode()

flag_pattern = (pad(fake_flag_pad, 128))

#print(flag_pattern)

flag_pattern=bytes_to_long(flag_pattern)



pattern=1<<888

#print(bin(pattern))



cc = c * inverse(pow(g,flag_pattern,p),p)%p

cc = pow(cc, inverse(pattern, q), p)

print(cc)

table = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f']

dic = dict()

gtemp= pow(g, 2**48, p)



for half_flag1 in tqdm(itertools.product(table, repeat=6)):

    half_flag1 = bytes_to_long(''.join(half_flag1).encode())

    temp = cc * powmod(gtemp, -(half_flag1), p) % p

    dic[temp] = half_flag1

for half_flag2 in tqdm(itertools.product(table, repeat=6)):

    half_flag2 = bytes_to_long(''.join(half_flag2).encode())

    temp = powmod(g, half_flag2, p)

    if temp in dic:

        print(long_to_bytes(dic[temp]) + long_to_bytes(half_flag2))