C++力扣题目509--斐波那契数 70--爬楼梯 746--最小花费爬楼梯

509. 斐波那契数

力扣题目链接(opens new window)

斐波那契数，通常用?F(n) 表示，形成的序列称为 斐波那契数列 。该数列由?0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1)?= 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1 给你n ，请计算 F(n) 。

示例 1：

• 输入：2
• 输出：1
• 解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

• 输入：3
• 输出：2
• 解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

• 输入：4
• 输出：3
• 解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

#思路

斐波那契数列大家应该非常熟悉不过了，非常适合作为动规第一道题目来练练手。

因为这道题目比较简单，可能一些同学并不需要做什么分析，直接顺手一写就过了。

但「代码随想录」的风格是：简单题目是用来加深对解题方法论的理解的。

通过这道题目让大家可以初步认识到，按照动规五部曲是如何解题的。

对于动规，如果没有方法论的话，可能简单题目可以顺手一写就过，难一点就不知道如何下手了。

所以我总结的动规五部曲，是要用来贯穿整个动态规划系列的，就像之前讲过二叉树系列的递归三部曲?(opens new window)，回溯法系列的回溯三部曲?(opens new window)一样。后面慢慢大家就会体会到，动规五部曲方法的重要性。

#动态规划

动规五部曲：

这里我们要用一个一维dp数组来保存递归的结果

1. 确定dp数组以及下标的含义

dp[i]的定义为：第i个数的斐波那契数值是dp[i]

1. 确定递推公式

为什么这是一道非常简单的入门题目呢？

因为题目已经把递推公式直接给我们了：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

1. dp数组如何初始化

题目中把如何初始化也直接给我们了，如下：

dp[0] = 0;
dp[1] = 1;

1. 确定遍历顺序

从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的

1. 举例推导dp数组

按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当N为10的时候，dp数组应该是如下的数列：

0 1 1 2 3 5 8 13 21 34 55

如果代码写出来，发现结果不对，就把dp数组打印出来看看和我们推导的数列是不是一致的。

以上我们用动规的方法分析完了，C++代码如下：

class Solution {
public:
    int fib(int N) {
        if (N <= 1) return N;
        vector<int> dp(N + 1);
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= N; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[N];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

当然可以发现，我们只需要维护两个数值就可以了，不需要记录整个序列。

代码如下：

class Solution {
public:
    int fib(int N) {
        if (N <= 1) return N;
        int dp[2];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= N; i++) {
            int sum = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = sum;
        }
        return dp[1];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

#递归解法

本题还可以使用递归解法来做

代码如下：

class Solution {
public:
    int fib(int N) {
        if (N < 2) return N;
        return fib(N - 1) + fib(N - 2);
    }
};

• 时间复杂度：O(2^n)
• 空间复杂度：O(n)，算上了编程语言中实现递归的系统栈所占空间

这个递归的时间复杂度大家画一下树形图就知道了，如果不清晰的同学，可以看这篇：通过一道面试题目，讲一讲递归算法的时间复杂度！(opens new window)

#总结

斐波那契数列这道题目是非常基础的题目，我在后面的动态规划的讲解中将会多次提到斐波那契数列！

这里我严格按照关于动态规划，你该了解这些！?(opens new window)中的动规五部曲来分析了这道题目，一些分析步骤可能同学感觉没有必要搞的这么复杂，代码其实上来就可以撸出来。

但我还是强调一下，简单题是用来掌握方法论的，动规五部曲将在接下来的动态规划讲解中发挥重要作用，敬请期待！

?

70. 爬楼梯

力扣题目链接(opens new window)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

• 输入： 2
• 输出： 2
• 解释： 有两种方法可以爬到楼顶。
  • 1 阶 + 1 阶
  • 2 阶

示例 2：

• 输入： 3
• 输出： 3
• 解释： 有三种方法可以爬到楼顶。
  • 1 阶 + 1 阶 + 1 阶
  • 1 阶 + 2 阶
  • 2 阶 + 1 阶

#思路

本题大家如果没有接触过的话，会感觉比较难，多举几个例子，就可以发现其规律。

爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法。

那么第一层楼梯再跨两步就到第三层 ，第二层楼梯再跨一步就到第三层。

所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来，那么就可以想到动态规划了。

我们来分析一下，动规五部曲：

定义一个一维数组来记录不同楼层的状态

1. 确定dp数组以及下标的含义

dp[i]： 爬到第i层楼梯，有dp[i]种方法

1. 确定递推公式

如何可以推出dp[i]呢？

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。

还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！

所以dp[i] = dp[i - 1] + dp[i - 2] 。

在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。

这体现出确定dp数组以及下标的含义的重要性！

1. dp数组如何初始化

再回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]种方法。

那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但基本都是直接奔着答案去解释的。

例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶。

但总有点牵强的成分。

那还这么理解呢：我就认为跑到第0层，方法就是0啊，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0.

其实这么争论下去没有意义，大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1。

从dp数组定义的角度上来说，dp[0] = 0 也能说得通。

需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。

所以本题其实就不应该讨论dp[0]的初始化！

我相信dp[1] = 1，dp[2] = 2，这个初始化大家应该都没有争议的。

所以我的原则是：不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。

1. 确定遍历顺序

从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

1. 举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

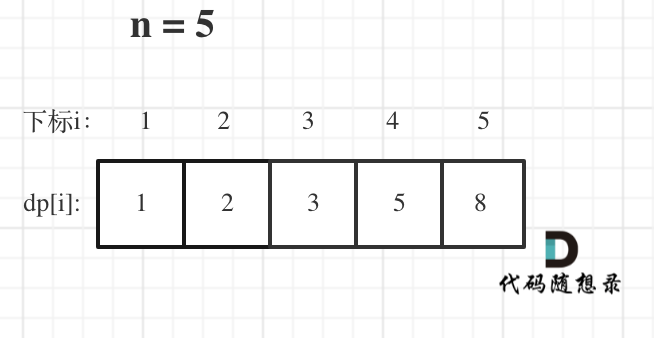
如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。

此时大家应该发现了，这不就是斐波那契数列么！

唯一的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！

以上五部分析完之后，C++代码如下：

// 版本一
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

当然依然也可以，优化一下空间复杂度，代码如下：

// 版本二
class Solution {
public:
    int climbStairs(int n) {
        if (n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

后面将讲解的很多动规的题目其实都是当前状态依赖前两个，或者前三个状态，都可以做空间上的优化，但我个人认为面试中能写出版本一就够了哈，清晰明了，如果面试官要求进一步优化空间的话，我们再去优化。

因为版本一才能体现出动规的思想精髓，递推的状态变化。

#拓展

这道题目还可以继续深化，就是一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法爬到n阶楼顶。

这又有难度了，这其实是一个完全背包问题，但力扣上没有这种题目，大家可以去卡码网去做一下?57. 爬楼梯(opens new window)

所以后续我在讲解背包问题的时候，今天这道题还会从背包问题的角度上来再讲一遍。 如果想提前看一下，可以看这篇:70.爬楼梯完全背包版本(opens new window)

这里我先给出本题的代码：

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) { // 把m换成2，就可以AC爬楼梯这道题
                if (i - j >= 0) dp[i] += dp[i - j];
            }
        }
        return dp[n];
    }
};

代码中m表示最多可以爬m个台阶。

以上代码不能运行哈，我主要是为了体现只要把m换成2，粘过去，就可以AC爬楼梯这道题，不信你就粘一下试试。

此时我就发现一个绝佳的大厂面试题，第一道题就是单纯的爬楼梯，然后看候选人的代码实现，如果把dp[0]的定义成1了，就可以发难了，为什么dp[0]一定要初始化为1，此时可能候选人就要强行给dp[0]应该是1找各种理由。那这就是一个考察点了，对dp[i]的定义理解的不深入。

然后可以继续发难，如果一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法爬到n阶楼顶。这道题目leetcode上并没有原题，绝对是考察候选人算法能力的绝佳好题。

这一连套问下来，候选人算法能力如何，面试官心里就有数了。

其实大厂面试最喜欢的问题就是这种简单题，然后慢慢变化，在小细节上考察候选人。

#总结

这道题目和动态规划：斐波那契数?(opens new window)题目基本是一样的，但是会发现本题相比动态规划：斐波那契数?(opens new window)难多了，为什么呢？

关键是?动态规划：斐波那契数?(opens new window)题目描述就已经把动规五部曲里的递归公式和如何初始化都给出来了，剩下几部曲也自然而然的推出来了。

而本题，就需要逐个分析了，大家现在应该初步感受出关于动态规划，你该了解这些！?(opens new window)里给出的动规五部曲了。

简单题是用来掌握方法论的，例如昨天斐波那契的题目够简单了吧，但昨天和今天可以使用一套方法分析出来的，这就是方法论！

所以不要轻视简单题，那种凭感觉就刷过去了，其实和没掌握区别不大，只有掌握方法论并说清一二三，才能触类旁通，举一反三哈！

746. 使用最小花费爬楼梯

力扣题目链接(opens new window)

旧题目描述：

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值?cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

示例?1：

• 输入：cost = [10, 15, 20]
• 输出：15
• 解释：最低花费是从 cost[1] 开始，然后走两步即可到阶梯顶，一共花费 15 。

示例 2：

• 输入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
• 输出：6
• 解释：最低花费方式是从 cost[0] 开始，逐个经过那些 1 ，跳过 cost[3] ，一共花费 6 。

提示：

• cost 的长度范围是 [2, 1000]。
• cost[i] 将会是一个整型数据，范围为 [0, 999] 。

#算法公开课

《代码随想录》算法视频公开课?(opens new window)：：动态规划开更了！| LeetCode：746. 使用最小花费爬楼梯?(opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

---

本题之前的题目描述是很模糊的，看不出来，第一步需要花费体力值，最后一步不用花费，还是说 第一步不花费体力值，最后一步花费。

后来力扣改了题目描述，新题目描述：

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

#思路

（在力扣修改了题目描述下，我又重新修改了题解）

修改之后的题意就比较明确了，题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的， 从 下标 0 下标1 开始跳就要花费体力了。

1. 确定dp数组以及下标的含义

使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了。

dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。

对于dp数组的定义，大家一定要清晰！

1. 确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。

dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？

一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

1. dp数组如何初始化

看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。

那么 dp[0] 应该是多少呢？ 根据dp数组的定义，到达第0台阶所花费的最小体力为dp[0]，那么有同学可能想，那dp[0] 应该是 cost[0]，例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话，dp[0] 就是 cost[0] 应该是1。

这里就要说明本题力扣为什么改题意，而且修改题意之后 就清晰很多的原因了。

新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的，但从 第0 个台阶 往上跳的话，需要花费 cost[0]。

所以初始化 dp[0] = 0，dp[1] = 0;

1. 确定遍历顺序

最后一步，递归公式有了，初始化有了，如何遍历呢？

本题的遍历顺序其实比较简单，简单到很多同学都忽略了思考这一步直接就把代码写出来了。

因为是模拟台阶，而且dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了。

但是稍稍有点难度的动态规划，其遍历顺序并不容易确定下来。 例如：01背包，都知道两个for循环，一个for遍历物品嵌套一个for遍历背包容量，那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢？ 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢？

这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的！

1. 举例推导dp数组

拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

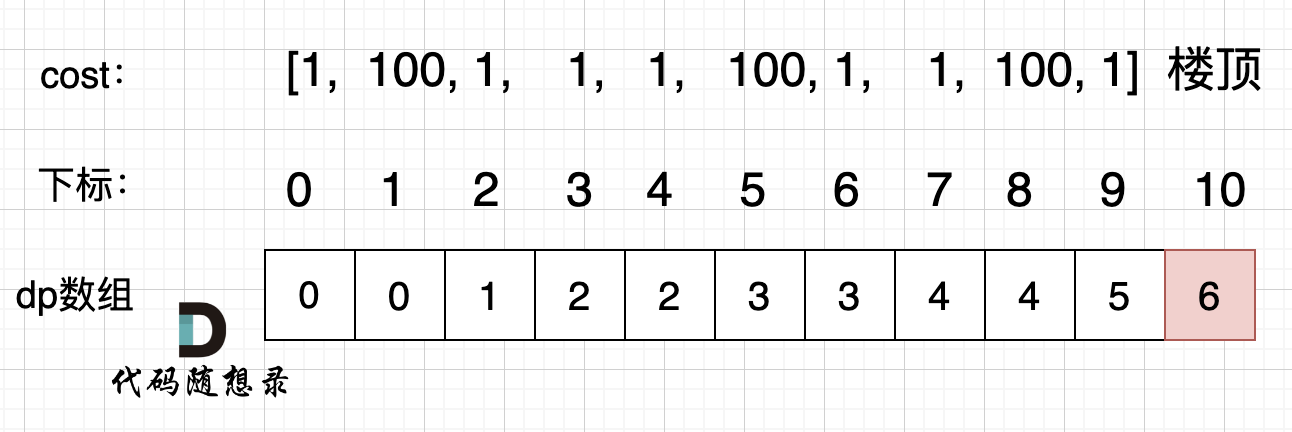
如果大家代码写出来有问题，就把dp数组打印出来，看看和如上推导的是不是一样的。

以上分析完毕，整体C++代码如下：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size() + 1);
        dp[0] = 0; // 默认第一步都是不花费体力的
        dp[1] = 0;
        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

还可以优化空间复杂度，因为dp[i]就是由前两位推出来的，那么也不用dp数组了，C++代码如下：

// 版本二
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0;
        int dp1 = 0;
        for (int i = 2; i <= cost.size(); i++) {
            int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
            dp0 = dp1; // 记录一下前两位
            dp1 = dpi;
        }
        return dp1;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

当然如果在面试中，能写出版本一就行，除非面试官额外要求 空间复杂度，那么再去思考版本二，因为版本二还是有点绕。版本一才是正常思路。

#拓展

旧力扣描述，如果按照 第一步是花费的，最后一步不花费，那么代码是这么写的，提交也可以通过

// 版本一
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size());
        dp[0] = cost[0]; // 第一步有花费
        dp[1] = cost[1];
        for (int i = 2; i < cost.size(); i++) {
            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        // 注意最后一步可以理解为不用花费，所以取倒数第一步，第二步的最少值
        return min(dp[cost.size() - 1], dp[cost.size() - 2]);
    }
};

当然如果对 动态规划 理解不够深入的话，拓展内容就别看了，容易越看越懵。

#总结

大家可以发现这道题目相对于 昨天的动态规划：爬楼梯?(opens new window)又难了一点，但整体思路是一样的。

从动态规划：斐波那契数?(opens new window)到?动态规划：爬楼梯?(opens new window)再到今天这道题目，录友们感受到循序渐进的梯度了嘛。

每个系列开始的时候，都有录友和我反馈说题目太简单了，赶紧上难度，但也有录友和我说有点难了，快跟不上了。

其实我选的题目都是有目的性的，就算是简单题，也是为了练习方法论，然后难度都是梯度上来的，一环扣一环。

但我也可以随便选来一道难题讲呗，这其实是最省事的，不用管什么题目顺序，看心情找一道就讲。

难的是把题目按梯度排好，循序渐进，再按照统一方法论把这些都串起来，所以大家不要催我哈，按照我的节奏一步一步来就行了