day01 深度学习介绍

发布时间：2024年01月22日

1.1深度学习介绍

1.2神经网络NN

1、概念：

（1）tensor 和 tensor相加。

1.1深度学习介绍

1、深度学习

? ? ? ? 机器学习的分支。人工神经网络为基础，对数据的特征进行学习的方法。

2、机器学习和深度学习的区别：

【特征抽取】：

机器学习：人工的特征抽取。
深度学习：自动的进行特征抽取。

【数据量】：

机器学习：数据少，效果不是很好
深度学习：数据多，效果更好

3、深度学习应用场景：

图像识别：物体识别、场景识别、人脸检测跟踪、人脸身份认证。
自然语言处理技术：机器翻译、文本识别、聊天对话。
语音技术：语音识别

4、深度学习框架：pytorch

目前企业常见的深度学习框架有很多：TensorFlow、Caffe2、Theano、Pytorch、Chainer、DyNet、MXNet等。

1.2神经网络NN

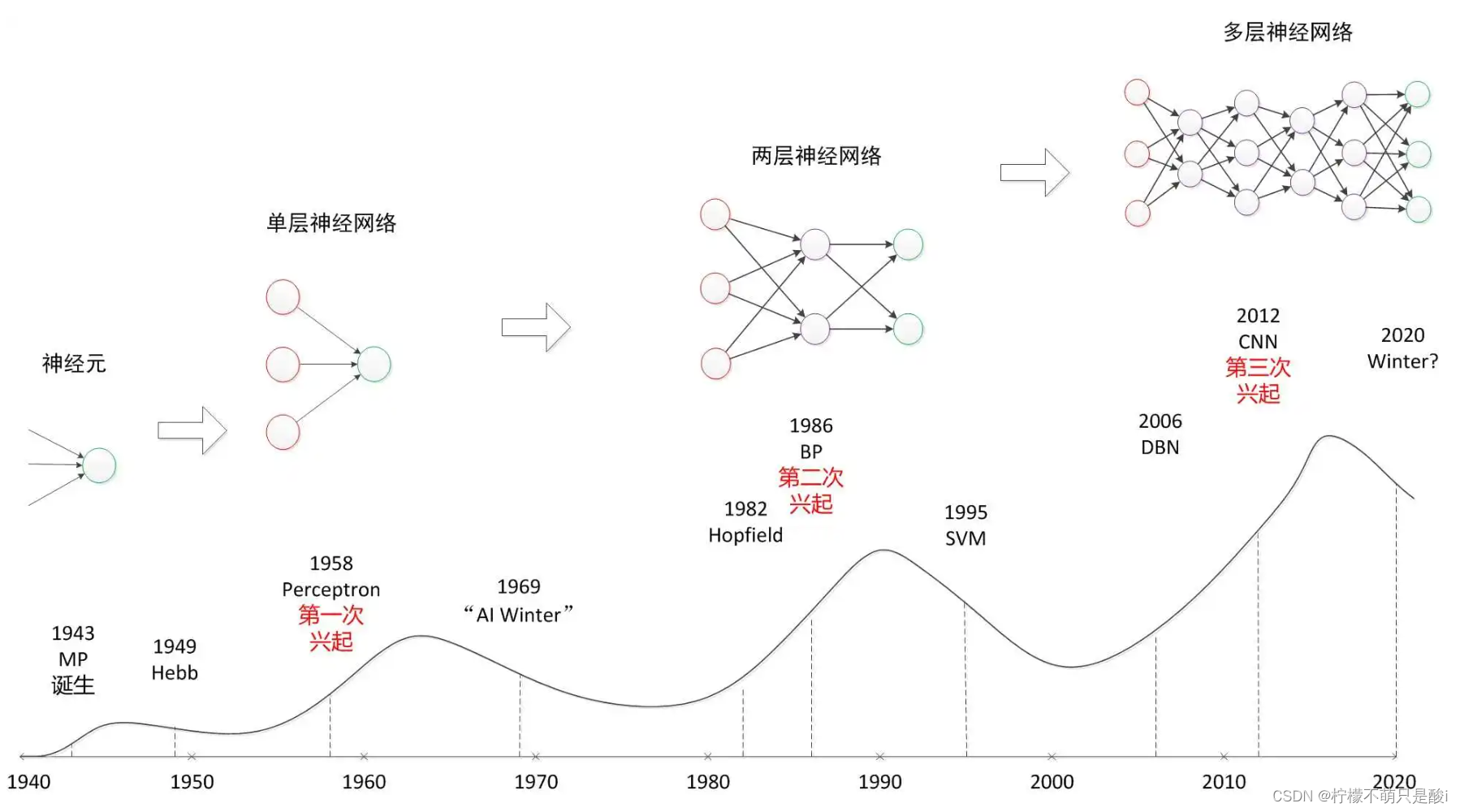
1、概念：

又称为人工神经网络ANN（Artificial Netural Network）。简称神经网络（NN）或类神经网络。模拟生物的神经系统，对函数进行估计或近似。

2、神经元

概念：神经网络中的基础单元，相互连接，组成神经网络。

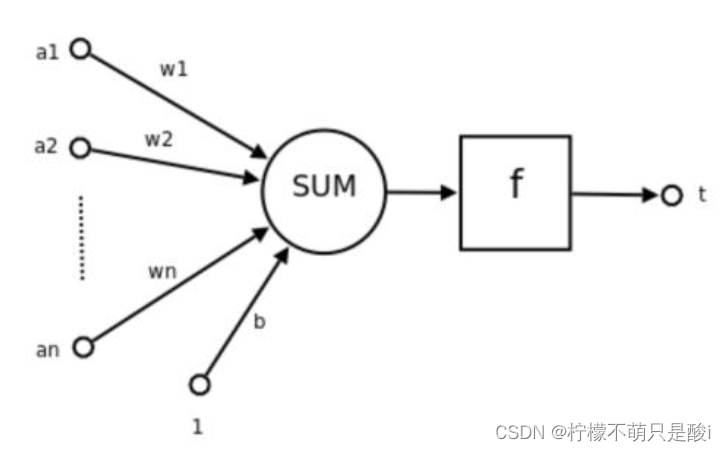
其中：

①a1、a2... an为各个输入的分量。

②w1、w2...wn为各个输入分量对应的权重参数。

③b为偏置

④f为激活函数。常见的激活函数有tanh、sigmoid、relu

⑤t为神经元的输出。

使用数学公式表示： $t = f(W^T A + b)$ ? ? ? 其中：? ? $W^{T}$ 表示W的转置

对公式的理解：输出 = 激活函数( 权重*输入求和?+ 偏置)

可见：一个神经元的功能是求得输入向量与权向量的内积后，经一个非线性传递函数得到一个标量结果。

3、（单层）神经网络

最简单的神经网络的形式。

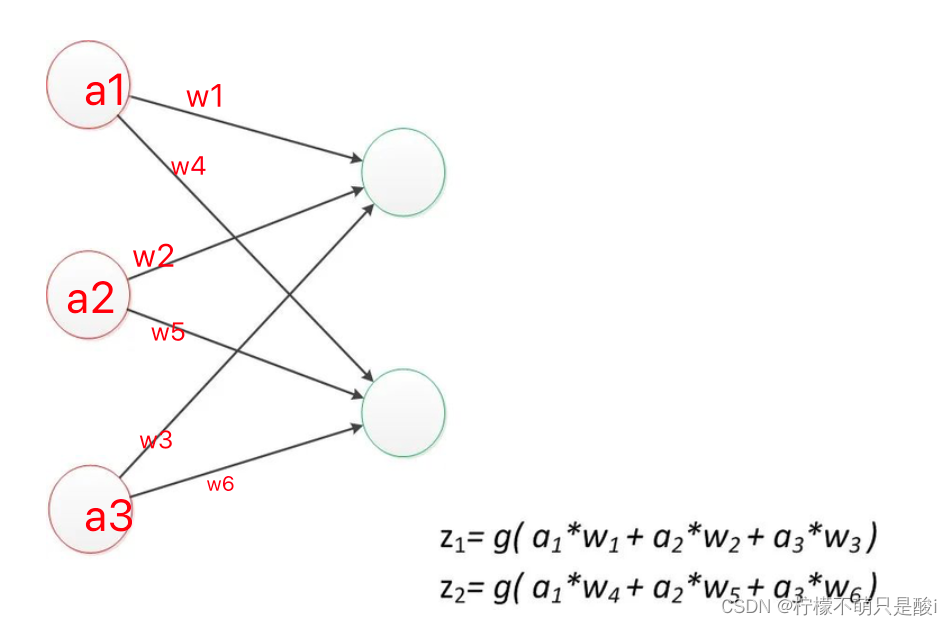
4、感知机（两层）

两层的神经网络。
简单的二分类的模型，给定阈值，判断数据属于哪一部分。

5、多层神经网络

输入层、
输出层、
隐藏层：可以有多层，每一层的神经元的个数可以不确定。

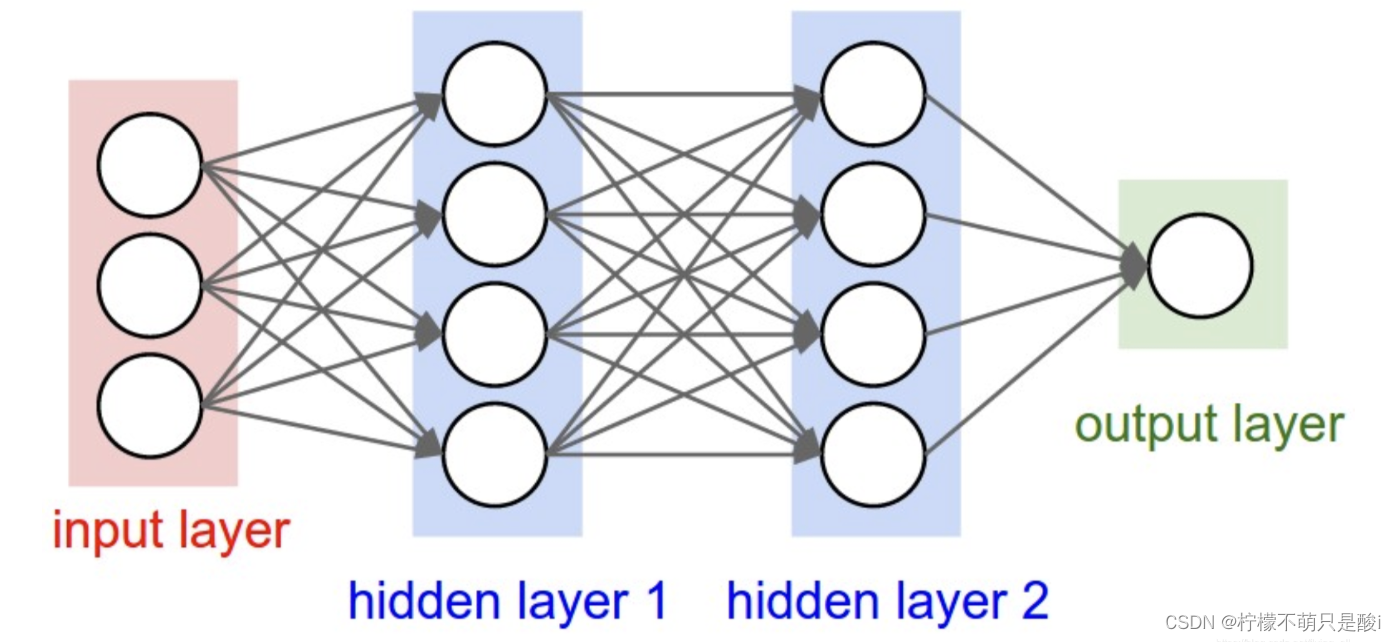
全连接层：当前层和前一层每个神经元相互连接，我们称当前这一层为全连接层。
即：第N层和第N-1层中的神经元两两之间都有连接。

进行的是 y = Wx + b

6、激活函数

作用：

增加模型的非线性分割能力。
提高模型稳健性
缓解梯度消失问题
加速模型收敛等。

（1）饱和与非饱和激活函数

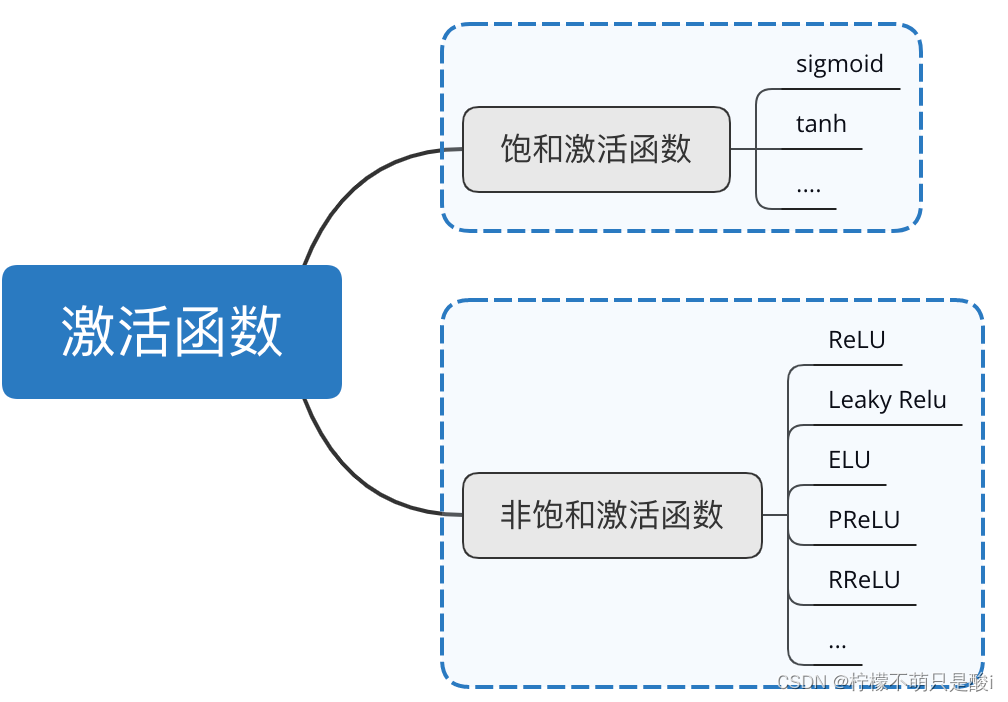
相对于饱和激活函数，使用非饱和激活函数的优势在于：

非饱和激活函数能解决深度神经网络（层数非常多）带来的梯度消失问题。
使用非饱和激活函数能加快收敛速度。

（2）饱和激活函数

①?Sigmoid激活函数

数学表达式为： $f (x) = \frac{1}{1+e^{-x}}$

求导： ${f}'(x)= f(x)(1-f(x))$

结果：输出值范围为（0,1）之间的实数。

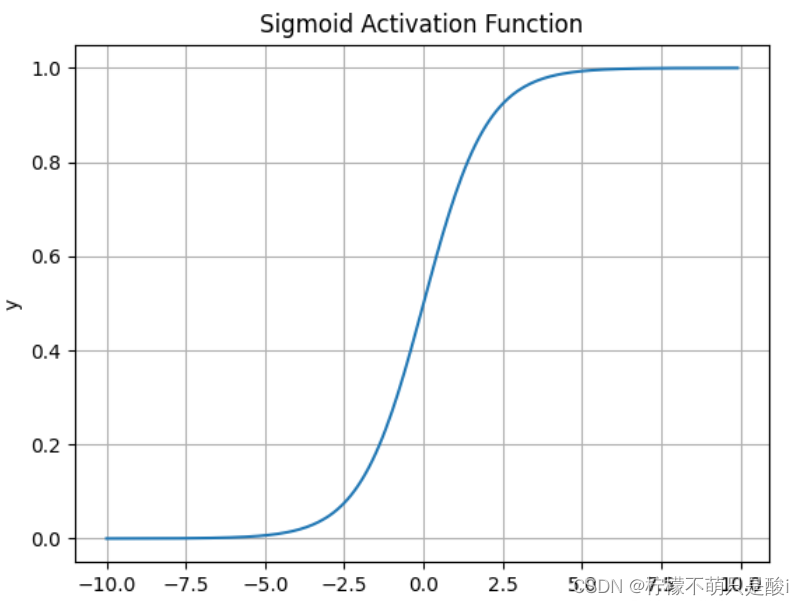
②?tanh激活函数

数学表达式为： $f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

实际上，Tanh函数是 sigmoid 的变形： $\tan h(x) = 2sigmoid(2x) - 1$

tanh是“零为中心”的。

结果：输出值范围为（-1,1）之间的实数。

（3）非饱和激活函数

① ??ReLU激活函数

数学表达式为： $f(x) = max(0,x)$

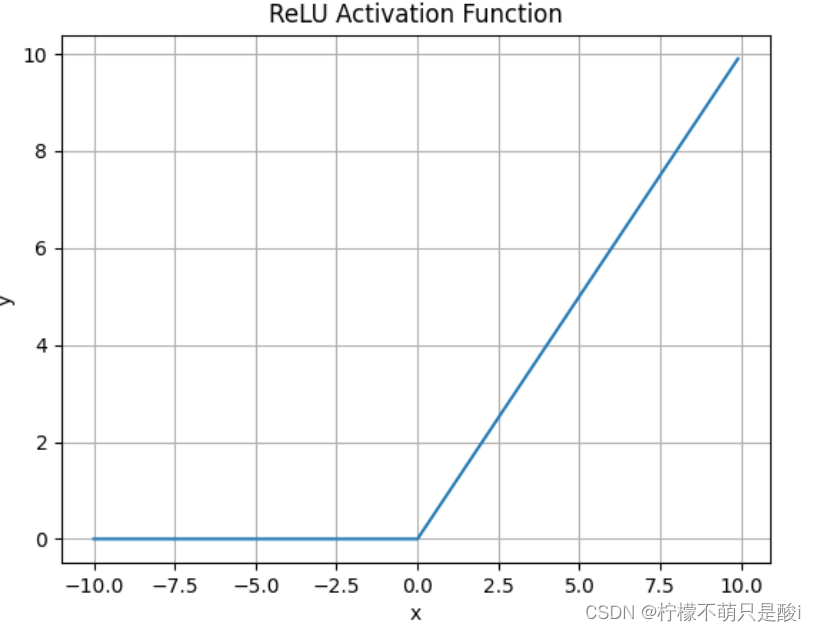
使用场景：

ReLU解决了梯度消失的问题，当输入值为正时，神经元不会饱和
由于ReLU线性、非饱和的性质，在SGD中能够快速收敛
计算复杂度低，不需要进行指数运算

缺点：

与Sigmoid一样，其输出不是以0为中心的

②?Leaky Relu激活函数

数学表达式为： $f(x) = max(ax,x)$

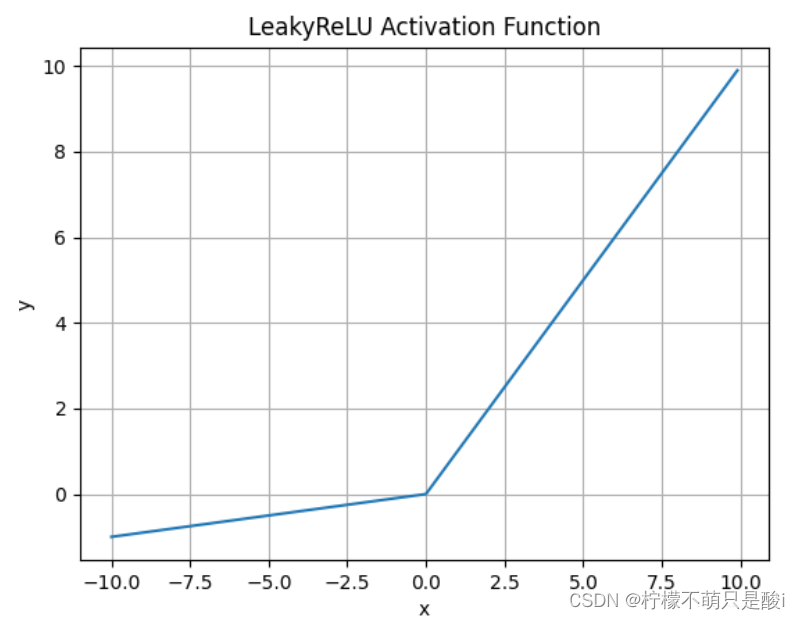
什么情况下适合使用Leaky ReLU？

解决了ReLU输入值为负时神经元出现的死亡的问题
Leaky?ReLU线性、非饱和的性质，在SGD中能够快速收敛
计算复杂度低，不需要进行指数运算

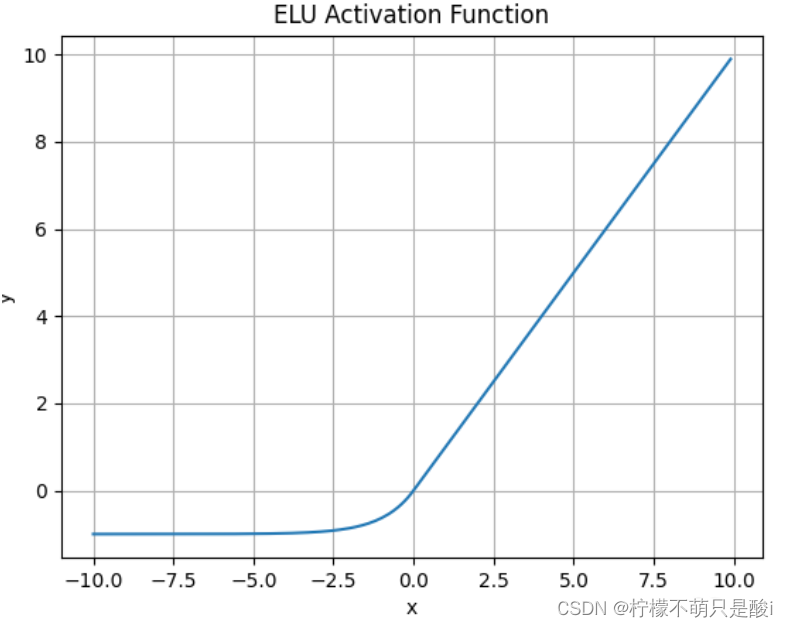
③ ELU激活函数

数学表达式为：

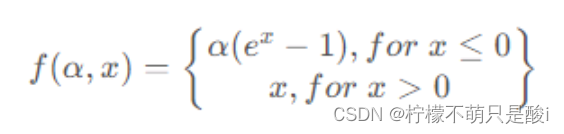
1.3pytorch安装+入门

1、pytorch安装

2、Tensor张量

各种数值数据称为张量。

0阶张量：常数 scaler

1阶张量：向量vector

2阶张量：矩阵matrix

3阶张量：...

3、张量的创建方法

打开jupyter，使用命令jupyter notebook

（1）使用python中的列表或者序列创建tensor

（2）使用numpy中的数组创建tensor

（3）使用torcch的api创建tensor

①torch.empty(3,4) 创建3行4列的空的tensor，会用无用数据进行填充。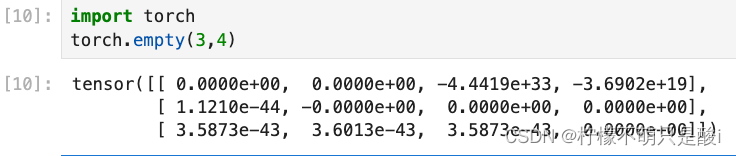

②torch.ones(3,4) 创建3行4列的全为1 的tensor

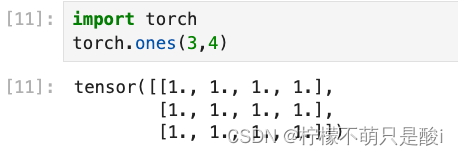
③torch.zeros(3,4) 创建3行4列的全为0的tensor

④torch.rand(3,4) 创建3行4列的随机值的tensor，随机值的区间是[0,1)

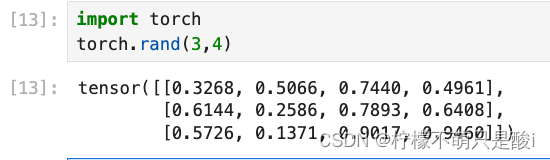
⑤torch.randint( low = 0,high = 10, size = [3,4]) 创建3行4列的随机整数的tensor，随机值的区间是[ low,high)

⑥torch.randn([3,4]) 创建3行4列的随机数的tensor ,随机值的分布均值为0，方差为1

(这里的randn ，n表示normal)

4、张量的方法和属性

（1）获取tensor中的数据（当tensor中只有一个元素可用）：tensor.item( )

（2）转化为numpy数组

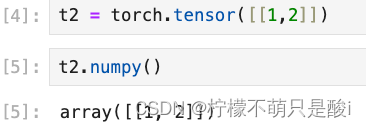
（3）获取形状：tensor.size()
tensor.size(0)? 获取第一个维度的形状

（4）形状改变：tensor.view((3,4)) 。类似numpy中的reshape，是一种浅拷贝，仅仅是形状发生改变。

（5）获取维数：tensor.dim()

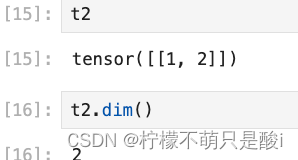
（6）获取最大值：tensor.max()

（7）转置：tensor.t()? ?二维

高维：tensor.transpose(1,2)? 将第一维度和第二维度交换、tensor.permute(0,2,1)

（8）获取tensor[1,3] 获取tensor中第一行第三列的值。（行和列的索引都是从0开始）

（9）tensor[1,3] 对tensor中第一行，第散列的位置进行赋值。

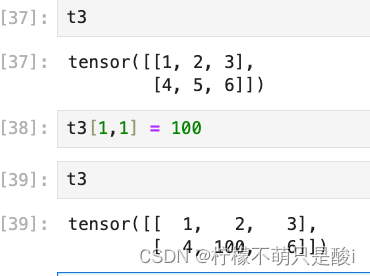
（10）tensor切片：

图片所示，取了第一列。

5、tensor的数据类型

（1）获取tensor 的数据类型：tensor.dtype

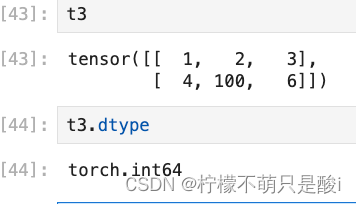
（2）创建数据的时候指定类型

（3）类型的修改

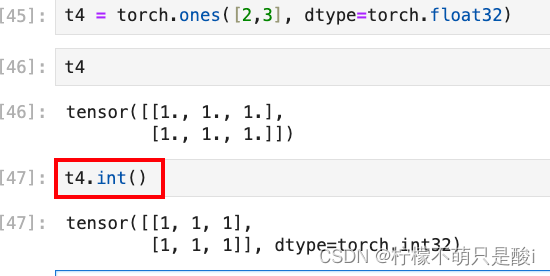
6、tensor的其他操作

（1）tensor 和 tensor相加。

x.add(y)? 不会直接修改x的值。

x.add_(y) 会直接修改x的值。??

（2）tensor和数字操作

（3）CUDA中的tensor

通过.to 方法能够把一个tensor转移到另外一个设备（比如从CPU转到GPU）

# 实例化device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 把tensor转化为CUDA支持的tensor，或者cpu支持的tensor
tensor.to(device)

1.4梯度下降和反向传播

1、梯度

概念：梯度是一个向量，导数+变化最快的方向（学习的前进方向）

回顾下机器学习：

? ? ? ?① 收集数据x，构建机器学习模型f，得到f(x，w) = Ypredict

? ? ? ? ②判断模型好坏的方法：

loss = (Ypredict - Ytrue)^2   （ 回归损失）
loss = Ytrue · log(Yredict)    (分类损失)

? ? ? ? ③目标：通过调整（学习）参数w，尽可能的降低loss。

2、梯度下降

算出梯度、

3、常见的导数的计算

链式法则、求偏导数、

4、反向传播

（1）前向传播：将训练集数据输入到ANN的输入层，经过隐藏层，最后到达输出层并输出结果。【输入层—隐藏层–输出层】

（2）反向传播：由于ANN的输入结果与输出结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层。【输出层–隐藏层–输入层】

（3）权重更新：在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。

5、使用Pytorch完成线性回归

（1）tensor(data, requires_grad = True)

① 该tensor后续会被计算梯度、tensor所有的操作都会被记录在grade_in?

② 当requires_grad = True时，tensor.data 和 tensor不相同。否则，得到是相同的结果。

（2）with torch.no_grad()

其中的操作不会被跟踪

（3）反向传播：output.backward()

（4）获取某个参数的梯度：x.grad? ?累加梯度，每次反向传播之前需要先把梯度置为0之后。

6、手动实现线性回归。

假设基础模型y=wx+b ，其中w和b均为参数，我们使用y = 3x+0.8 来构造数据x，y，所以最后通过模型应该能够得出w和b应该分别接近3和0.8。

（1）准备数据（2）计算预测值
（3）计算损失，把参数的梯度置为0，进行反向传播（4）更新参数

import torch
import matplotlib.pyplot as plt
learning_rate = 0.01  # 定义一个学习率

# 1、准备数据
"""
y = wx + b
y = 3x + 0.8
"""
x = torch.rand([100, 1])
y_true = x*3 + 0.8

# 2、通过模型计算 y_project
w = torch.rand([1, 1], requires_grad=True)
b = torch.tensor(0, requires_grad=True, dtype=torch.float32)

# 4、通过循环，反向传播，更新参数
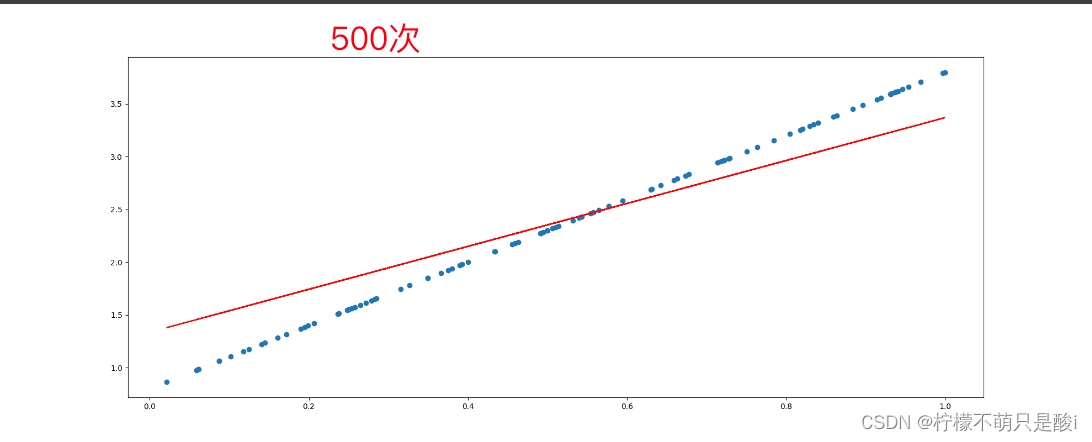
for i in range(500):
    # 3、计算loss
    y_predict = torch.matmul(x, w) + b
    loss = (y_true - y_predict).pow(2).mean()  # 平方，再均值

    if w.grad is not None:     # 将梯度置为0
        w.grad.data.zero_()
    if b.grad is not None:
        b.grad.data.zero_()

    loss.backward()   # 反向传播
    w.data = w.data - learning_rate * w.grad
    b.data = b.data - learning_rate * b.grad
    print(f"w:{w.item()},b:{b.item()},loss:{loss.item()}")

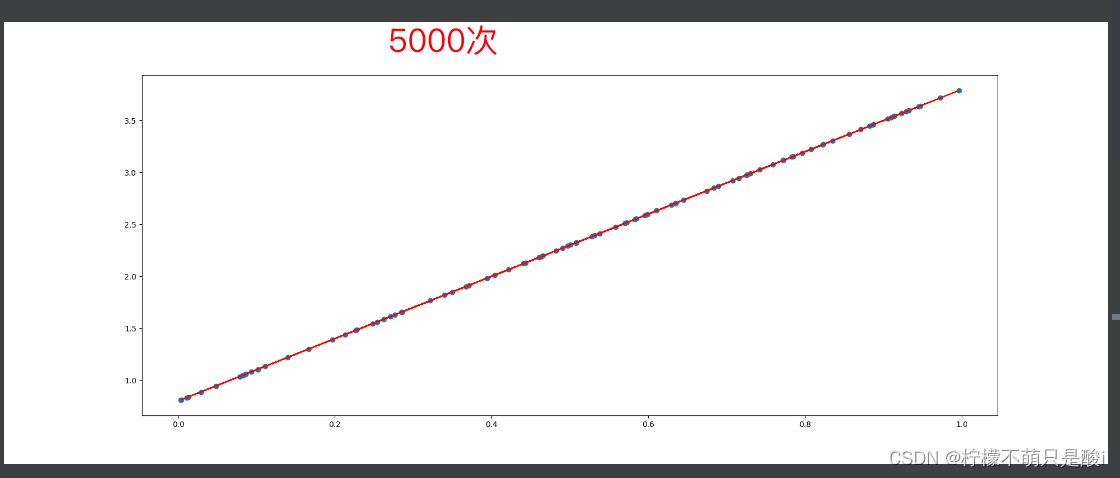
# 画图
plt.figure(figsize=(20, 8))
plt.scatter(x.numpy().reshape(-1), y_true.numpy().reshape(-1))
y_predict = torch.matmul(x, w) + b
plt.plot(x.numpy().reshape(-1), y_predict.detach().reshape(-1), c='r')
plt.show()

7、nn.Module?

nn.Module 是torch.nn提供的一个类，是pytorch 中我们自定义网络的一个基类，在这个类中定义了很多有用的方法，让我们在继承这个类定义网络的时候非常简单。

文章来源:https://blog.csdn.net/Miss_liangrm/article/details/135665458
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！