【备战蓝桥杯】快来学吧~ 图论巩固，Delia的生物考试

蓝桥杯备赛 | 洛谷做题打卡day12

• 最大食物链计数

  题目背景

  你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

  题目描述

  给你一个食物网，你要求出这个食物网中最大食物链的数量。

  （这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

  Delia 非常急，所以你只有 $1$ 秒的时间。

  由于这个结果可能过大，你只需要输出总数模上 $80112002$ 的结果。

  输入格式

  第一行，两个正整数 $n、m$，表示生物种类 $n$ 和吃与被吃的关系数 $m$。

  接下来 $m$ 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

  输出格式

  一行一个整数，为最大食物链数量模上 $80112002$ 的结果。

  样例 #1

  样例输入 #1

  5 7
  1 2
  1 3
  2 3
  3 5
  2 5
  4 5
  3 4
  

  样例输出 #1

  5
  

  提示

  各测试点满足以下约定：

  

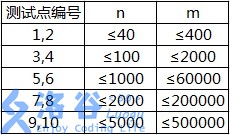
  【补充说明】

  数据中不会出现环，满足生物学的要求。

题解代码

学会利用新知，自己多试试并尝试积攒一些固定解答方案，debug，以下是题解代码 ~

总的思路：拓扑排序

这里具体讲一下为什么要用拓扑排序（思维过程）：

1、这是一道图论题；

2、不是求最短路；

3、根据提示“最左端是不会捕食其他生物的生产者”可以想到，我们要入度为零的点开始查找；

4、再看一遍题目，就是求路径数，当且仅当一个点的入度变为零时才需要入队，并不是数据更新一次就要入队；

5、出度为零的点的路径总数和就是答案。

思路已经呼之欲出了：拓扑排序！

---

下面讲讲如何实现。

拓扑排序的精髓就在于每个点只会入队一次，每条边只会通过一次，所以时间复杂度就有很好的保证O(N+M)，SPFA的玄学时间复杂度）。

正确性说明：题目的补充说明告诉我们这是一张DAG（有向无环图），因此必定存在一个入度为0的点，也因此每一个点都会被遍历。

当一个点的入度变为零，即所有它能吃的东西都已经搜索过了，这是它的数值就不会发生变化，就可以入队了。这样保证了队列里的所有数值都不会发生变化。

#include<bits/stdc++.h>
using namespace std;
int n,m,ru[5005],chu[5005],a,b,f[5005],ans;
int mp[5005][5005];
queue<int> q;
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		scanf("%d%d", &a, &b);
		mp[a][b]=1;//记录关系
		chu[a]++;
		ru[b]++;//记录入度和出度
	}
	for(int i=1;i<=n;i++){
		if(ru[i]==0) {
			f[i]=1;
			q.push(i);//入度为零的入队
		}
	}
	while(!q.empty()){//队列不为空
		int a=q.front();
		q.pop();//出队
		for(int k=1;k<=n;k++){
			if(mp[a][k]==0)continue;
			f[k]+=f[a];//更新
			f[k]%=80112002;
			ru[k]--;//食物少了一个
			if(ru[k]==0){//入队为零才入队
				if(chu[k]==0){
					ans+=f[k];
					ans%=80112002;
                    continue;//有没有都行
				}
				q.push(k);
			}
		}
	}
	cout<<ans; 
}

简单来说，因为任务可以并发，所以一个任务如果有前驱的话，最优方案便是在它的最晚一个前驱结束后就立即开始，而且任务k的前驱节点一定小于k，所以读入时顺便从它的前驱里挑一个最大的转移即可。同时可以更新最终答案。

我的一些话

• 今天给大家复习一下这几天都在学习的图论算法，关于图的遍历确实有一定难度，需要通盘的考虑和理解，以及扎实的数据结构基础才能独立写出AC代码。但无论难易，大家都要持续做题，保持题感喔！一起坚持(o′ω`o)

• 如果有非计算机专业的uu自学的话，关于数据结构的网课推荐看b站上青岛大学王卓老师的课，讲的很细致，有不懂都可以私信我喔

• 总结来说思路很重要，多想想，多在草稿纸上画画，用测试数据多调试，debug后成功编译并运行出正确结果真的会感到很幸福！

• 关于之前蓝桥杯备赛的路线和基本方法、要掌握的知识，之前的博文我都有写，欢迎大家关注我，翻阅自取哦~

• 不管什么都要坚持吧，三天打鱼两天晒网无法形成肌肉记忆和做题思维，该思考的时候一定不要懈怠，今天就说这么多啦，欢迎评论留言，一起成长：）