【分块模板】P2068统计和

??题目传送门：统计和 - 洛谷

题目大意

给定一个长度为?n，初始值都为?0?的序列?，有w次操作，每次操作：

x a b 表示将a的值加上b，y a b 表示查询a到b的数字和。

思路

这题其实有很多做法，包括线段树、树状数组等。

但大家既然是来看板子的，那就用分块的写法。先画个图理解一下：

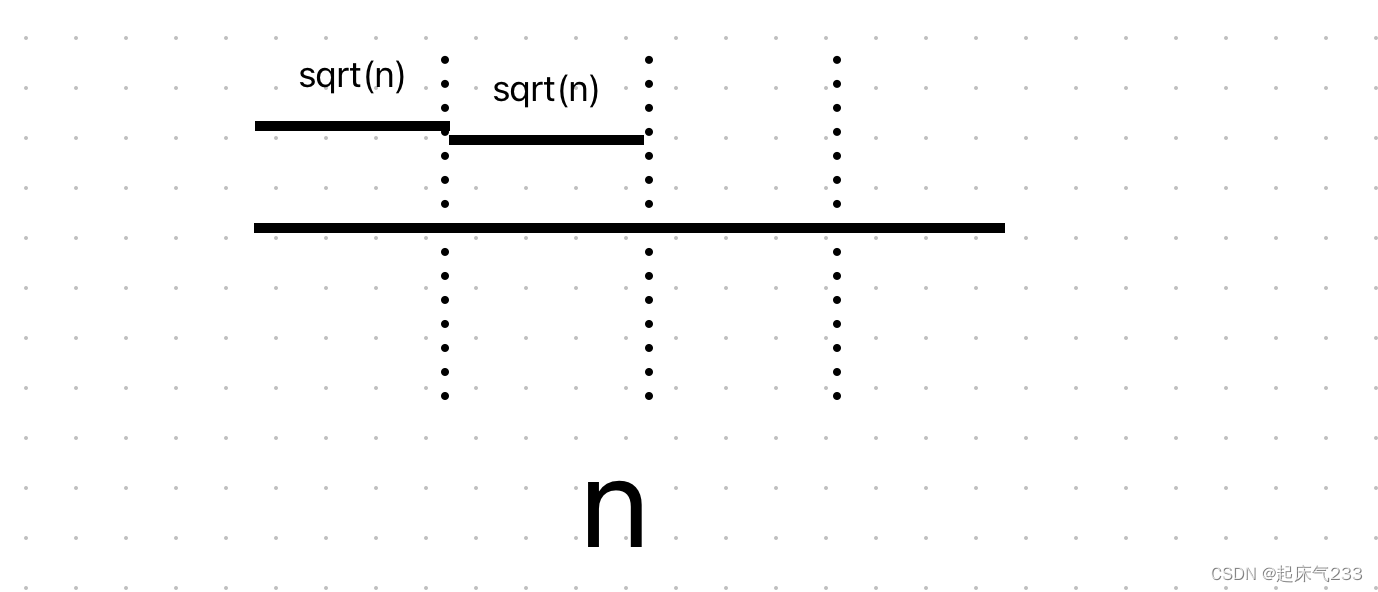
这里，我们把n分成了? ?块，对于其中的每一块，我们都可以直接用for循环求出其区间和。

那查询怎么做呢？分三种情况：

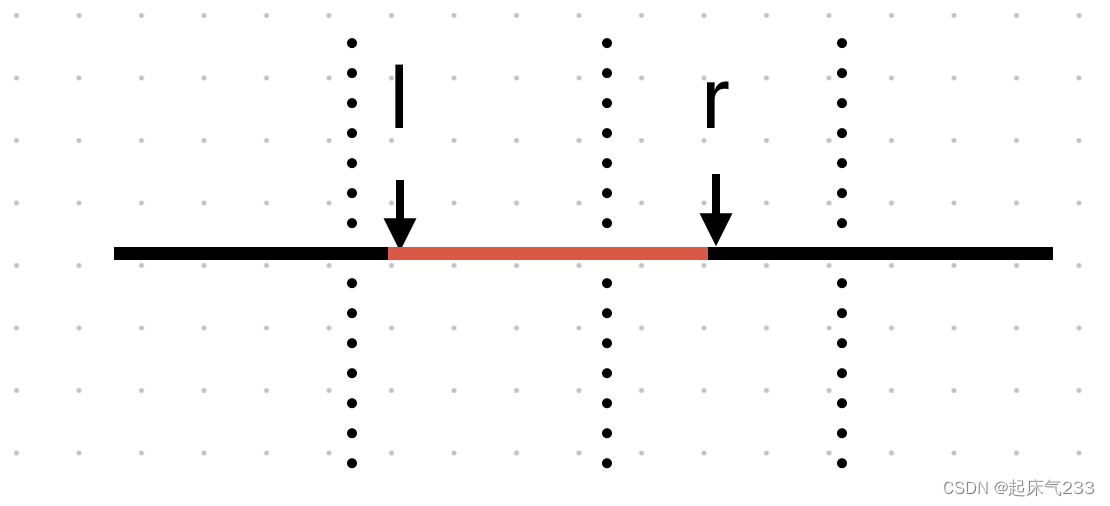
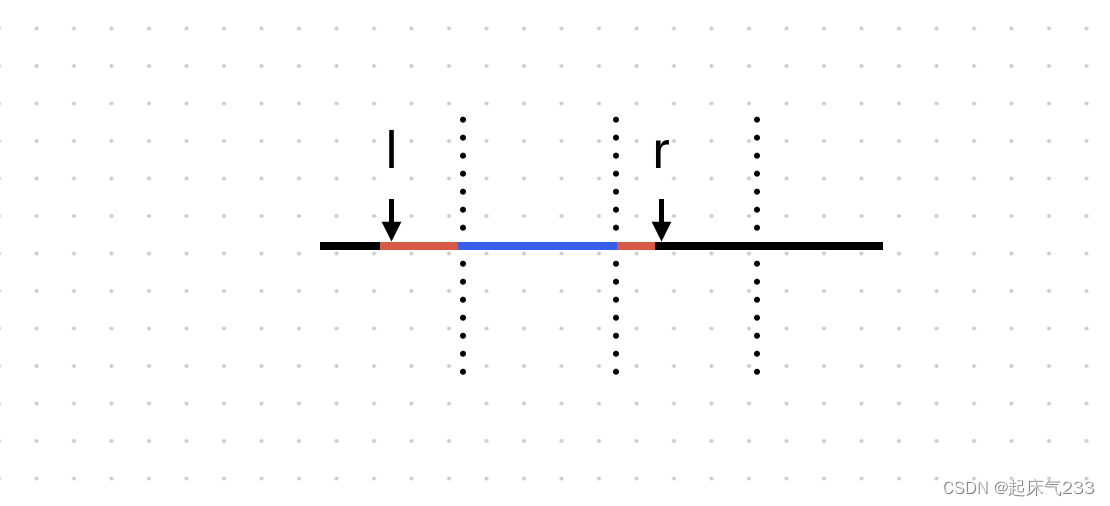
三种情况中，红色部分可以直接用for循环求，而蓝色部分则是通过访问单个块内的区间和得到的

代码

#include<iostream>
#include<cmath>
using namespace std;
#define MaxN 100005
#define MaxB 320
#define For(i, j, k) for(int i = j; i <= k; i++)
#define int long long

int n, bs, mb;
//bs:每个块的大小；mb：块的数量
int block[MaxN], a[MaxN];
//block[i]：第i个点所属的块
int l[MaxB], r[MaxB];
//l[i]/r[i]:第i个块左端点和右端点
long long Sum[MaxB];

void init(){
	bs = sqrt(n);
	For(i, 1, n){
		block[i] = (i-1) / bs + 1;
		Sum[block[i]] += a[i];
	}
	mb = (n-1) / bs + 1;
	For(j, 1, mb){            //计算每个块的左右端点
		l[j] = (j-1) * bs + 1;
		r[j] = j * bs;
	}
	r[mb] = n;
}

int query(int x, int y){        //查询[x, y]区间的总和
	int ans = 0;
	if(block[x] == block[y]){    
		For(i, x, y) ans += a[i];    //两边直接相加
	} else{
		For(i, block[x]+1, block[y]-1) ans += Sum[i];
		For(i, x, r[block[x]]) ans += a[i];
		For(i, l[block[y]], y) ans += a[i];
	}
	return ans;
}

void modify(int x, int y){        //将x改为y
	a[x] += y; Sum[block[x]] = 0;    
	For(i, l[block[x]], r[block[x]])
		Sum[block[i]] += a[i];
}

signed main()
{
	int q, x, y;
    char op;
	cin >> n;
	For(i, 1, n) a[i] = 0;
	init();
	cin >> q;
	while(q--){
		cin >> op >> x >> y;
		if(op == 'y') cout << query(x, y) << endl;
		else modify(x, y);
	}
	return 0;
}

总结

各个数据结构的模板题，

即区间查询、单点修改的区间求和问题，可以说是入门数据结构的基础了，十分重要。

最后，如果你觉得这篇文章还不错，可以点个关注点个赞，这是免费的，你可以随时取消。你的支持永远是作者最大的动力！感谢大家的观看，我们下次见！