攀登者2 - 华为OD统一考试

OD统一考试

分值： 200分

题解： Java / Python / C++

题目描述

攀登者喜欢寻找各种地图，并且尝试攀登到最高的山峰。

地图表示为一维数组，数组的索引代表水平位置，数组的元素代表相对海拔高度。其中数组元素0代表地面。

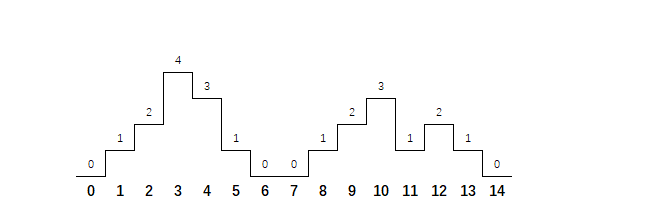
例如：[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0]，代表如下图所示的地图，地图中有两个山脉位置分别为 1,2,3,4,5 和 8,9,10,11,12,13，最高峰高度分别为 4,3。最高峰位置分别为3,10。

一个山脉可能有多座山峰(高度大于相邻位置的高度，或在地图边界且高度大于相邻的高度)。

登山时会消耗登山者的体力(整数)，

• 上山时，消耗相邻高度差两倍的体力
• 下山时，消耗相邻高度差一倍的体力
• 平地不消耗体力

登山者体力消耗到零时会有生命危险。

例如，上图所示的山峰：

• 从索引0，走到索引1，高度差为1，需要消耗 2 * 1 = 2 的体力，
• 从索引2，走到索引3，高度差为2，需要消耗 2 * 2 = 4 的体力。
• 从索引3，走到索引4，高度差为1，需要消耗 1 * 1 = 1 的体力。

攀登者想要评估一张地图内有多少座山峰可以进行攀登，且可以安全返回到地面，且无生命危险。

例如：上图中的数组，有3个不同的山峰，登上位置在3的山可以从位置0或者位置6开始，从位置0登到山顶需要消耗体力 1 * 2 + 1 * 2 + 2 * 2 = 8，从山顶返回到地面0需要消耗体力 2 * 1 + 1 * 1 + 1 * 1 = 4 的体力，按照登山路线 0 → 3 → 0 需要消耗体力12。攀登者至少需要12以上的体力（大于12）才能安全返回。

输入描述

第一行输入为地图一维数组

第二行输入为攀登者的体力

输出描述

确保可以安全返回地面，且无生命危险的情况下，地图中有多少山峰可以攀登。

示例1

输入：
0,1,2,4,3,1,0,0,1,2,3,1,2,1,0
13

输出：
3

说明：
3，10，12 都可安全到达。

示例2

输入：
1,4,3
999

输出：
0

说明：
没有合适的起点和终点

题解

这是一个通过动态规划求解的问题，主要思路如下：

1. 首先，遍历一次数组，计算每个位置到左侧最近的地面的向上和向下的总高度差，分别存储在 left_up 和 left_down 数组中。
2. 然后，从右向左遍历数组，计算每个峰值的上山和下山的最小体力消耗，并判断是否满足攀登者的体力条件。
3. 最后，统计满足条件的峰值个数。

这个算法的时间复杂度为 O(n)，其中 n 是数组的长度

Java

import java.util.Arrays;
import java.util.Scanner;
/**
 * @author code5bug
 */
public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // 读取地图高度数组
        int[] heights = Arrays.stream(scanner.nextLine().split(","))
                .mapToInt(Integer::parseInt)
                .toArray();
        int n = heights.length;
        int power = scanner.nextInt();

        // 初始化数组用于记录从左侧最近的地面到当前位置的向上和向下的总高度差
        int[] leftUp = new int[n + 1];
        int[] leftDown = new int[n + 1];
        Arrays.fill(leftUp, Integer.MAX_VALUE);
        Arrays.fill(leftDown, Integer.MAX_VALUE);

        int prevHeight = -1;
        // 从左向右遍历地图，计算左侧最近的地面到当前位置的向上和向下的总高度差
        for (int i = 1; i <= n; i++) {
            int curHeight = heights[i - 1];
            if (curHeight == 0) {
                leftUp[i] = 0;
                leftDown[i] = 0;
            } else if (leftUp[i - 1] != Integer.MAX_VALUE) {
                int d = Math.abs(curHeight - prevHeight);
                if (curHeight >= prevHeight) {
                    leftUp[i] = leftUp[i - 1] + d;
                    leftDown[i] = leftDown[i - 1];
                } else {
                    leftUp[i] = leftUp[i - 1];
                    leftDown[i] = leftDown[i - 1] + d;
                }
            }
            prevHeight = curHeight;
        }

        int peakCount = 0;

        // 初始化变量用于记录从右侧最近的地面到当前位置的向上和向下的总高度差
        int rightUp = Integer.MAX_VALUE;
        int rightDown = Integer.MAX_VALUE;
        // 从右向左遍历地图
        for (int r = n - 1; r >= 0; r--) {
            if (heights[r] == 0) {
                rightUp = 0;
                rightDown = 0;
            } else if (rightUp != Integer.MAX_VALUE) {
                int d = Math.abs(heights[r] - heights[r + 1]);
                if (heights[r] > heights[r + 1]) {
                    rightUp += d;
                } else {
                    rightDown += d;
                }
            }

            // 当前位置为峰值时，计算上山和下山的最小体力消耗，并判断是否满足攀登者的体力条件
            if ((r == 0 || heights[r - 1] < heights[r]) && (r + 1 == n || heights[r] > heights[r + 1])) {
                int minUpCost = Integer.MAX_VALUE;
                int minDownCost = Integer.MAX_VALUE;
                if (leftUp[r + 1] != Integer.MAX_VALUE) {
                    minUpCost = Math.min(leftUp[r + 1] * 2 + leftDown[r + 1], minUpCost);
                    minDownCost = Math.min(leftUp[r + 1] + leftDown[r + 1] * 2, minDownCost);
                }
                if (rightUp != Integer.MAX_VALUE) {
                    minUpCost = Math.min(minUpCost, rightUp * 2 + rightDown);
                    minDownCost = Math.min(minDownCost, rightUp + rightDown * 2);
                }

                if (minUpCost != Integer.MAX_VALUE && minUpCost + minDownCost < power) {
                    // System.out.println(r + "可安全到达");
                    peakCount++;
                }
            }
        }

        // 输出满足条件的峰值个数
        System.out.println(peakCount);
    }
}

Python

from math import inf


heights = list(map(int, input().split(",")))
power = int(input())

n = len(heights)

# left_up[i] 表示从左侧最近的地面出发到达当前位置需要向上走的总高度差
# left_down[i] 表示从左侧最近的地面出发到达当前位置需要向下走的总高度差
left_up, left_down = [inf] * (n + 1), [inf] * (n + 1)
prev_hegiht = -1
for i, cur_height in enumerate(heights, start=1):
    if cur_height == 0:  # 可以作为起点
        left_up[i], left_down[i] = 0, 0
    elif left_up[i-1] != inf:  # 可达非起点
        d = abs(cur_height - prev_hegiht)
        if cur_height >= prev_hegiht:  # 向上
            left_up[i], left_down[i] = left_up[i-1] + d, left_down[i-1]
        else:
            left_up[i], left_down[i] = left_up[i-1], left_down[i-1] + d
    else:  # 表示当前位置左侧不可到达 (左侧没有合适的起点)
        pass
    prev_hegiht = cur_height

peak_count = 0

# 从右往左侧走
right_up, right_down = inf, inf
for r in range(n - 1, -1, -1):
    if heights[r] == 0:
        right_up, right_down = 0, 0
    elif right_up != inf:
        d = abs(heights[r] - heights[r+1])
        if heights[r] > heights[r+1]:  # 向上
            right_up += d
        else:
            right_down += d

    # 当前 r 为峰值时
    if (r == 0 or heights[r - 1] < heights[r]) and (r + 1 == n or heights[r] > heights[r + 1]):
        min_up_cost, min_down_cost = inf, inf
        if left_up[r + 1] != inf:
            min_up_cost = min(left_up[r + 1] * 2 + left_down[r + 1], min_up_cost)
            min_down_cost = min(left_up[r + 1] + left_down[r + 1] * 2, min_down_cost)
        if right_up != inf:
            min_up_cost = min(min_up_cost, right_up * 2 + right_down)
            min_down_cost = min(min_down_cost, right_up + right_down * 2)
        if min_up_cost + min_down_cost < power:
            # print(f"山峰{r}可达， 上山最小消耗：{min_up_cost} ， 下山最小消耗： {min_down_cost}")
            peak_count += 1

print(peak_count)

C++

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

int main() {
    vector<int> heights;
    int height, power;
    while(cin >> height) {
        heights.push_back(height);
        if(cin.peek() == ',') {
            cin.ignore();
        } else { // 读取攀登者体力
            cin >> power;
            break;
        }
    };

    int n = heights.size();

    // left_up[i] 表示从左侧最近的地面出发到达当前位置需要向上走的总高度差
    // left_down[i] 表示从左侧最近的地面出发到达当前位置需要向下走的总高度差
    vector<int> left_up(n + 1, INT_MAX);
    vector<int> left_down(n + 1, INT_MAX);
    int prevHeight = -1;

    // 从左向右遍历地图，计算左侧最近的地面到当前位置的向上和向下的总高度差
    for (int i = 1; i <= n; i++) {
        int curHeight = heights[i - 1];

        if (curHeight == 0) {
            left_up[i] = 0;
            left_down[i] = 0;
        } else if (left_up[i - 1] != INT_MAX) {
            int d = abs(curHeight - prevHeight);

            if (curHeight >= prevHeight) {
                left_up[i] = left_up[i - 1] + d;
                left_down[i] = left_down[i - 1];
            } else {
                left_up[i] = left_up[i - 1];
                left_down[i] = left_down[i - 1] + d;
            }
        }
        prevHeight = curHeight;
    }

    int peakCount = 0;

    // 初始化变量用于记录从右侧最近的地面到当前位置的向上和向下的总高度差
    int right_up = INT_MAX, right_down = INT_MAX;

    // 从右向左遍历地图
    for (int r = n - 1; r >= 0; r--) {
        if (heights[r] == 0) {
            right_up = 0;
            right_down = 0;
        } else if (right_up != INT_MAX) {
            int d = abs(heights[r] - heights[r + 1]);

            if (heights[r] > heights[r + 1]) {
                right_up += d;
            } else {
                right_down += d;
            }
        }

        if ((r == 0 || heights[r - 1] < heights[r]) && (r + 1 == n || heights[r] > heights[r + 1])) {
            int minUpCost = INT_MAX;
            int minDownCost = INT_MAX;

            if (left_up[r + 1] != INT_MAX) {
                minUpCost = min(left_up[r + 1] * 2 + left_down[r + 1], minUpCost);
                minDownCost = min(left_up[r + 1] + left_down[r + 1] * 2, minDownCost);
            }

            if (right_up != INT_MAX) {
                minUpCost = min(minUpCost, right_up * 2 + right_down);
                minDownCost = min(minDownCost, right_up + right_down * 2);
            }

            if (minUpCost != INT_MAX && minUpCost + minDownCost < power) {
                peakCount++;
            }
        }
    }

    // 输出结果
    cout << peakCount << endl;

    return 0;
}

🙏整理题解不易， 如果有帮助到您，请给点个赞 ???? 和收藏 ?，让更多的人看到。🙏🙏🙏