【数据结构】非递归实现快速排序与归并排序
发布时间:2024年01月17日
递归是可以向非递归进行变化的:
比如很经典的斐波那契数列可以用递归实现也可以用循环实现
但是有些复杂的递归仅仅依靠循环是很难控制的,
所以我们需要借助数据结构中的栈与队列帮助我们用非递归模拟递归,
故有的时候我们说非递归不是递归却胜似递归
通过本文可以更好的对比来理解两者不同之处
快速排序的非递归:
先说结论,我们会使用栈来模拟快速排序的递归----栈所在的文章。
注意:下图所使用的单趟排序为前后指针法----前后指针法所在文章。
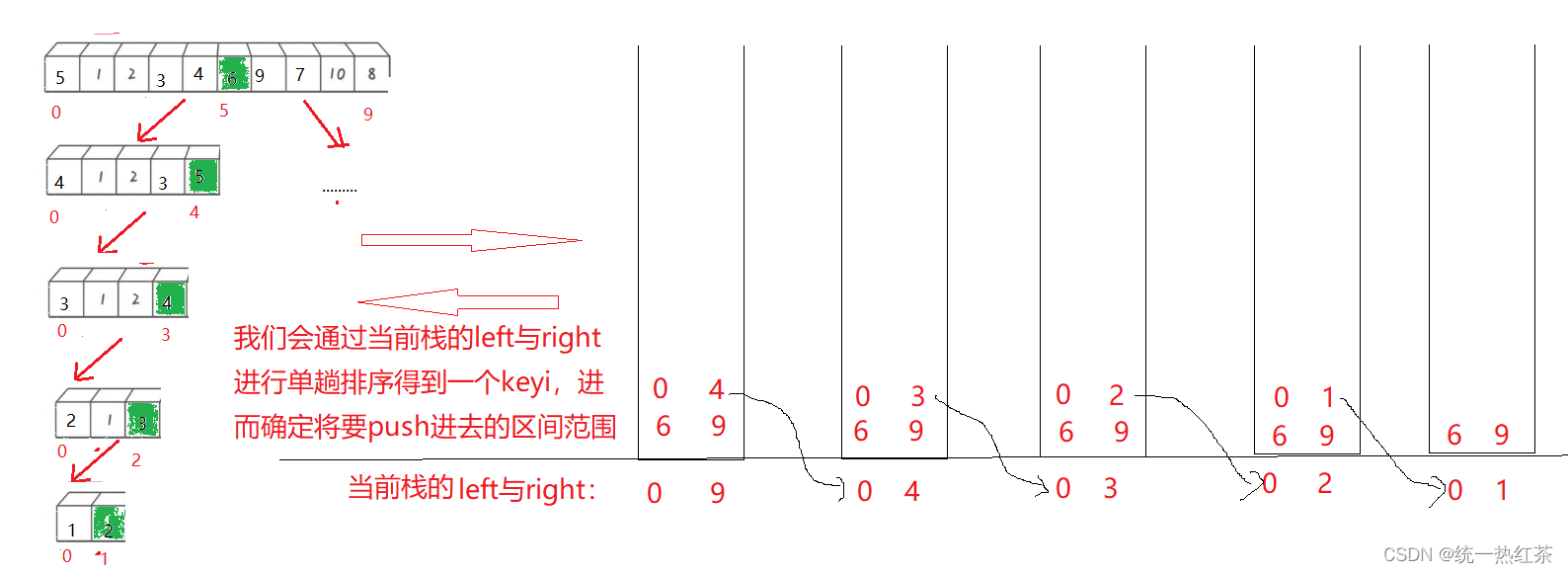
注意:
- 我们选择先压右边,这样
StackTop得到的就是左边,因为栈先进后出的原理 - 虽然我们自己造的栈push一次只能存储一个数据,但是我们push两次就可以解决这个问题
图示就很好的展示了如何用栈来模拟递归的过程。
可以与代码相互进行加强理解:
代码:
//前后指针
int PartSort(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int key = a[left];
while (cur <= right)
{
if (a[cur] < key)
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[prev], &a[left]);
return prev;
}
void QuickSortNonR(int* a, int begin, int end)
{
Stack s;
StackInit(&s);
StackPush(&s, end);
StackPush(&s, begin);
while (!StackEmpty(&s))
{
int left = StackTop(&s);
StackPop(&s);
int right = StackTop(&s);
StackPop(&s);
int keyi = PartSort(a, left, right);
//[begin keyi-1] [keyi+1 right]
if (keyi + 1 < right)
{
StackPush(&s, right);
StackPush(&s, keyi + 1);
}
if (left < keyi - 1)
{
StackPush(&s, keyi - 1);
StackPush(&s, left);
}
}
StackDestroy(&s);
}
归并排序的非递归:
那么归并是否也是使用栈来模拟呢?
答案是否定的,同时队列也是错误的
因为我们发现:
快排的模拟递归是
前序,即递下来的过程就完成了排序,不需要归回去。
而归并排序的思想呢?
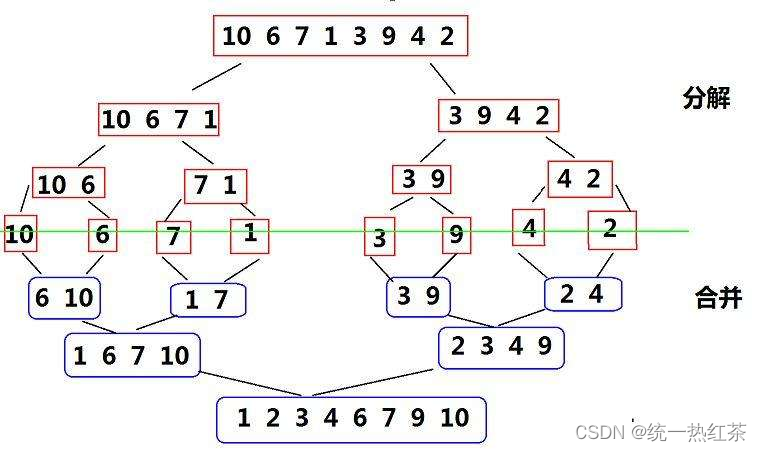
在递的时候只是完成了分组,每一组是返回条件的最小单元,还没有进行归并,
归并的过程是在分组之后完成的,是一种后序的思想
故我们当然不能用栈来模拟归并,即使可以达到分组的效果,那之后呢?
这里我们选择使用数组,需要一个额外的数组,空间复杂度仍然是O(N)
那我们是如何进行模拟的呢?
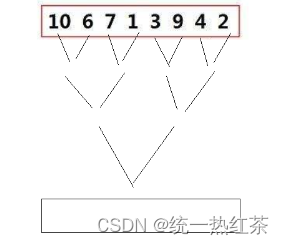
这张图就比较好的体现了非递归的思想,直接进行归并,这就要求我们要对数组的下标使用的比较灵活。
我们使用gap作为每一组(有序的组)的元素个数
先来看一次归并的代码,虽然长,但是分开来看就比较一目了然
这一部分是对下标的控制,
我们完成这一部分再嵌套一个控制gap的循环就得到完整的代码
int gap = 1;
int j = 0;
for (int i = 0; i < n; i += (2 * gap))
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = end1 + 1, end2 = begin2 + gap - 1;
这一部分是防止数组越界的操作,
当end1与begin2越界我们break即可
因为当上两者越界时,我们所在的区间已经有序,不需要排序
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
... 接下来是进行两者合并的逻辑
}
这是两个”数组”进行合并的逻辑
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
代码:
void MergerSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += (2 * gap))
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = end1 + 1, end2 = begin2 + gap - 1;
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(tmp);
}
文章来源:https://blog.csdn.net/2301_78636079/article/details/135657576
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Qt/C++音视频开发61-多屏渲染/一个解码渲染到多个窗口/画面实时同步
- 使用CDN防范SQL注入攻击:速盾网络(Sudun)的综合解决方案
- 虎克:开发小程序要多少钱一个,非专业开发如何做自己的小程序
- 使用yum/dnf管理软件包
- JavaSec基础 反射修改Final修饰的属性及绕过高版本反射限制
- 10年数据分析师整理,电商数据采集电商数据分析这么做,领导不重用你都难!
- python小技巧
- 2023-12-22 linux C语言pthread_kill函数,pthread_kill(tid, 0)可以用来判断线程是否存在
- imgaug库指南(13):从入门到精通的【图像增强】之旅
- 乐意购项目前端开发 #4