计算样本距离常见的集中度量方法

当计算两个样本之间的距离时，我们可以使用不同的距离度量方法，具体的选择通常取决于数据的性质以及任务的要求。以下是一些常见的距离度量方法：

1. 欧氏距离（Euclidean Distance）

欧氏距离是最常见的距离度量方法，适用于连续型数据。对于样本向量 x 和 y，欧氏距离的计算公式为：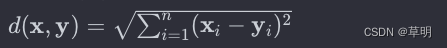

2. 曼哈顿距离（Manhattan Distance）

曼哈顿距离是两点之间沿坐标轴的绝对距离之和，适用于城市街区的距离计算。对于样本向量 x 和 y，曼哈顿距离的计算公式为：

3. 切比雪夫距离（Chebyshev Distance）

切比雪夫距离是两个样本向量在各个维度上差异的最大值，适用于离散型数据。对于样本向量 x 和 y，切比雪夫距离的计算公式为：

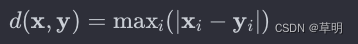
4. 闵可夫斯基距离（Minkowski Distance）

闵可夫斯基距离是欧氏距离和曼哈顿距离的一般化，适用于多种数据类型。对于样本向量 x 和 y，计算公式为：

当 p=2 时，即为欧氏距离；当 p=1 时，即为曼哈顿距离。

5. 余弦相似度（Cosine Similarity）

余弦相似度度量两个向量方向上的相似程度，适用于文本等高维稀疏数据。对于样本向量 x 和 y，计算公式为：

6. 汉明距离（Hamming Distance）

汉明距离度量两个等长字符串在对应位置上不同的位数，适用于处理二进制数据。对于样本向量 x 和 y，计算公式为：

7. Jaccard相似度（Jaccard Similarity）： Jaccard相似度度量两个集合的相似程度，适用于处理集合数据。对于样本集合 A 和 B，计算公式为：

选择合适的距离度量方法取决于你的数据类型和任务需求。在实际应用中，可能需要尝试不同的距离度量方法，并根据实验效果来选择最适合的方法。