leetcode238:除自身以外数组的乘积

在leetcode上刷到了这一题，一开始并没有想到好的解题思路，写篇博客再来梳理一下吧。

题目要求：

• 不使用除法
• 在O(n)时间复杂度内

1.使用除法（违背题意）

该方法分以下几步:

1. 先遍历数组，求数组所有元素的乘积sum
2. 再遍历一遍数组，使用sum除以该下标对应的元素，将结果放在answer数组中

#include<stdio.h>
#include<stdlib.h>
int* productExceptSelf(int* nums, int numsSize, int* returnSize) {
    int* answer = (int*)calloc(numsSize, sizeof(int));
    *returnSize = numsSize;
    int sum = 1;
    for (int i = 0; i < numsSize; i++)
    {
        sum *= nums[i]; //求所有元素的乘积
    }
    for (int i = 0; i < numsSize; i++)
    {
        answer[i] = sum / nums[i];
    }
    return answer;
}

int main()
{
	int arr[] = { 1,2,3,4 };
	int sz = sizeof(arr) / sizeof(arr[0]);
    int count = 0;
    int* ret = productExceptSelf(arr, sz, &count);
    for (int i = 0; i < count; i++)
    {
        printf("%d", *(ret + i));
        if (i != count - 1)
        {
            printf(",");
        }
    }
    free(ret);
    ret = NULL;
	return 0;
}

2.左右乘积列表

相较于第一种方法，我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。这也是题目中暗示我们的

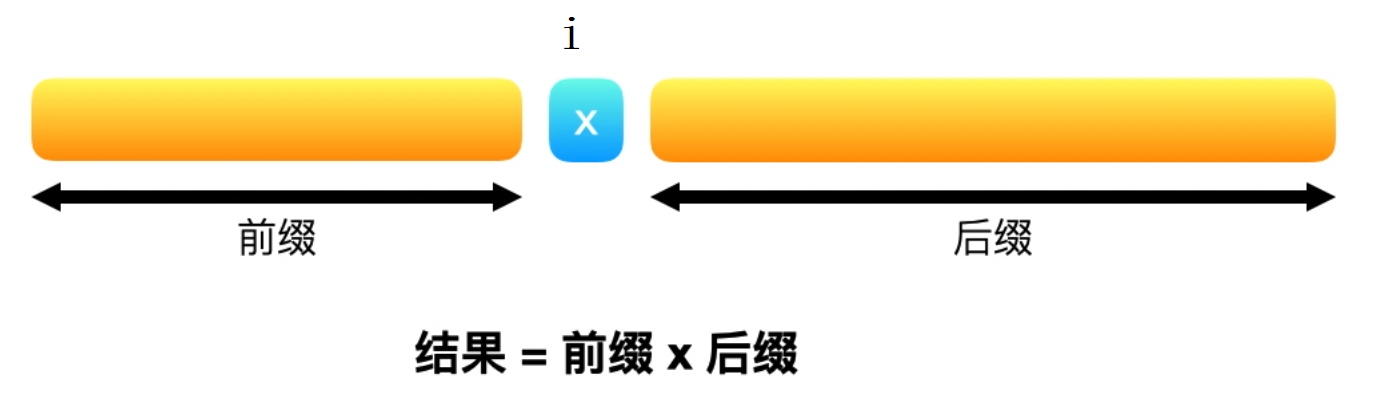
该方法分以下几步：

• 初始化两个空数组 Left 和 Right。对于给定下标 i，Left[i] 代表的是 i 左侧所有数字的乘积，Right[i] 代表的是 i 右侧所有数字的乘积。
• 对于数组 Left，Left[0] 应该是 1，因为第一个元素的左边没有元素。对于数组 Right，Right[length-1] 应为 1,因为最后一个元素右侧没有元素。（length 指的是输入数组的大小）
• 对于其它的元素，Left[i] = Left[i-1] * nums[i-1] （i从1开始 i++）

• 对于其它的元素，Right[i] = Right[i+1] * nums[i+1] （i从length-2开始 i–）

• 当 Left 和 Right 数组填充完成，我们只需要在输入数组上迭代：answer[i] = Left[i] * Righti]

#include<stdio.h>
#include<stdlib.h>
int* productExceptSelf(int* nums, int numsSize, int* returnSize) {
    int* answer = (int*)calloc(numsSize, sizeof(int));
    *returnSize = numsSize;
    int Left[numsSize];
    int Right[numsSize];
    Left[0] = 1;
    Right[3] = 1;
    for (int i = 1; i < numsSize; i++)
    {
        Left[i] = Left[i - 1] * nums[i - 1];
    }
    for (int i = 2; i >= 0; i--)
    {
        Right[i] = Right[i + 1] * nums[i + 1];
    }
    for (int i = 0; i < numsSize; i++)
    {
        answer[i] = Left[i] * Right[i];
    }
    return answer;
}

int main()
{
	int arr[] = { 1,2,3,4 };
	int sz = sizeof(arr) / sizeof(arr[0]);
    int count = 0;
    int* ret = productExceptSelf(arr, sz, &count);
    for (int i = 0; i < count; i++)
    {
        printf("%d", *(ret + i));
        if (i != count - 1)
        {
            printf(",");
        }
    }
    free(ret);
    ret = NULL;
	return 0;
}

复杂度分析：

• 时间复杂度：O(N)，其中 N 指的是数组 nums 的大小。预处理 Left 和 Right 数组以及最后的遍历计算都是 O(N)的时间复杂度。
• 空间复杂度：O(N)，其中 N 指的是数组 nums 的大小。使用了 Left 和 Right 数组去构造答案，Left 和 Right 数组的长度为数组 nums 的大小。

3.空间复杂度为O(1)的方法

由于输出数组不算在空间复杂度内，而且我们的answer数组只有最后才被用到，所以我们可以先将 Left 或 Right 数组用answer数组来计算。
该方法分为以下几步：

• 先把answer数组当作 Left数组来计算，然后再动态构造 Right 数组得到结果。这样我们就节省了两个数组，空间复杂度就为O(1)了。
• 动态构造Right数组我们只使用一个变量R就可以了，该变量初始化为1。R * nums[i] 即可得到最终的结果.

#include<stdio.h>
#include<stdlib.h>
int* productExceptSelf(int* nums, int numsSize, int* returnSize) {
    int* answer = (int*)calloc(numsSize, sizeof(int));
    *returnSize = numsSize;
    int left[numsSize];
    int right[numsSize];
    answer[0] = 1;
    int R = 1;
    //先求前缀之积
    for (int i = 1; i < numsSize; i++)
    {
        answer[i] = answer[i - 1] * nums[i - 1];
    }
    //求后缀之积与answer
    for (int i = numsSize - 1; i >= 0; i--)
    {
        // 对于下标 i，左边的乘积为 answer[i]，右边的乘积为 R
        answer[i] = answer[i] * R;
        // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
        R *= nums[i];
    }
    return answer;
}

int main()
{
	int arr[] = { 1,2,3,4 };
	int sz = sizeof(arr) / sizeof(arr[0]);
    int count = 0;
    int* ret = productExceptSelf(arr, sz, &count);
    for (int i = 0; i < count; i++)
    {
        printf("%d", *(ret + i));
        if (i != count - 1)
        {
            printf(",");
        }
    }
    free(ret);
    ret = NULL;
	return 0;
}

复杂度分析

• 时间复杂度：O(N)，其中 NNN 指的是数组 nums 的大小。分析与方法一相同。
• 空间复杂度：O(1)，输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。

目前想到的方法就这些，后续想到会补充。