LeetCode刷题--- 子集

?个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

• 力扣递归算法题【 ?http://t.csdnimg.cn/yUl2I?? 】
• 【C++】? ? ? ? ? 【 ?http://t.csdnimg.cn/6AbpV?】
• 数据结构与算法【 ?http://t.csdnimg.cn/hKh2l??】

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的 ?

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

子集

题目链接：子集

题目

给你一个整数数组?nums?，数组中的元素?互不相同?。返回该数组所有可能的子集（幂集）。

解集?不能?包含重复的子集。你可以按?任意顺序?返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums?中的所有元素?互不相同

---

解法

题目解析

题目意思很简单，给我们一个数组，返回其?所有可能的子集

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

---

算法原理思路讲解????

解法一

?

决策树就是我们后面设计函数的思路

---

?二、设计代码

（1）全局变量

vector<vector<int>> ret;
 vector<int> path;

（2）设计递归函数

void dfs(vector<int>& nums, int pos);

---

解法二?

一、画出决策树

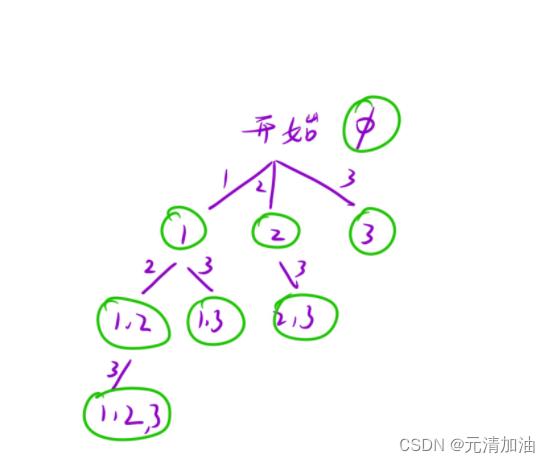
决策树就是我们后面设计函数的思路

---

?二、设计代码

（1）全局变量

vector<vector<int>> ret;
 vector<int> path;

1.递归函数头设计

void dfs(vector<int>& nums, int pos);

参数：nums 数组，pos 在数组中的位置?

?

---

代码实现

解法一

时间复杂度：O(n×2^n)。一共 2^n个状态，每种状态需要 O(n) 的时间来构造子集。

空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n)。

class Solution
{
 vector<vector<int>> ret;
 vector<int> path;
public:

    void dfs(vector<int>& nums, int pos)
    {
        if(pos == nums.size())
        {
            ret.push_back(path);
            return;
        }
        // 选
        path.push_back(nums[pos]);
        dfs(nums, pos + 1);
        path.pop_back(); // 恢复现场
        // 不选
        dfs(nums, pos + 1);
    }
    
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums, 0);
        return ret;
    }
    
};

---

解法二

class Solution
{
 vector<vector<int>> ret;
 vector<int> path;
 public:
    vector<vector<int>> subsets(vector<int>& nums) 
    {
    
        dfs(nums, 0);
        return ret;
    }
    void dfs(vector<int>& nums, int pos)
    {
        ret.push_back(path);
        for(int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            dfs(nums, i + 1);
            path.pop_back(); // 恢复现场
        }
    }
};