洛谷：集合与前缀和

1.亲戚(并查集)

#include<iostream>
using namespace std;
int n,m,p;
int m1,m2,p1,p2;
int f[5005];

int find(int x)//查询根节点，根节点的标志是根节点的父节点是自己
{
   if(f[x]!=x)f[x]=find(f[x]);//路径压缩，父节点变为根节点,方便下次询问
   return f[x];
}
void combine(int a,int b)
{
   f[find(a)]=find(b);
}
int main()
{
   cin>>n>>m>>p;
   for(int i=1;i<=n;i++)
	f[i]=i;//先让每个节点的父节点是自己
	for(int i=1;i<=m;i++)
	{
	    cin>>m1>>m2;
	    combine(m1,m2);//是两个集合的合并，让一个集合的根节点的父节点等于另外一个集合的根节点
	}
	for(int i=1;i<=p;i++)  
    {
      cin>>p1>>p2;
      if(find(p1)==find(p2))cout<<"Yes"<<endl;
      else cout<<"No"<<endl;
    }

? ? ? ? 从题目中来看，这是一对一对的亲戚关系，具有亲戚关系的是一个集合，如果两个集合中有同一个人，说明另外两个人也有亲戚关系，那他们就应该合并这两个集合，这不就是并查集支持的操作吗？我们定义一个父节点数组表示i节点的父节点，先让每个节点的父节点是自己，当两个人是亲戚时，我们就合并两个集合，让一个集合的根节点的父节点等于另外一个集合的根节点，循环结束后，具有亲戚关系的都在同一个集合里，如果两个人所在集合的根节点是相同的，这两个人就是亲戚，否则不是。

2.团伙(并查集)

#include<iostream>
using namespace std;
int n,m,p,q,f[100010],cnt=0;
int rsp[1010][1010];//定义一个二维数组表示两个人是否是敌人
char opt;
int find(int x)
{
	if(f[x]!=x) f[x]=find(f[x]);
	return f[x];
}
void combine(int a,int b)
{
	f[find(a)]=find(b);
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<=m;i++)
	{
		cin>>opt>>p>>q;
		if(opt=='F')combine(p,q),cnt++;
        else if(opt=='E')
        {
          rsp[p][q]=rsp[q][p]=1;
          for(int j=1;j<=n;j++)
         {
           if(rsp[q][j]==1)combine(p,j),cnt++;
           if(rsp[p][j]==1)combine(q,j),cnt++;
         }
        } 
    }
   cout<<cnt;
   return 0;
}

? ? ?这道题其实和上一道是基本上一样的，唯一不同的是这道题当两个人是敌人的时候我们怎么进行记录，是朋友就把把两个集合合并，如果是敌人，我们定义一个二维数组，如果p和q是敌人，则rsp[p][q]=rsp[q][p]=1，表示两个人是敌人，?当我们遍历时，如果q和j或者p和j是敌人，那p和j或者q和j就是朋友，合并两个集合即可，最后统计出有多少个集合，返回cnt。

3.字符串哈希(哈希表)

#include<iostream>
#include<set>
using namespace std;
set<string>word;
int n,cnt;
string str;
int main()
{
  cin>>n;
  while(n--)
  {
    cin>>str;
    word.insert(str);
  }
  for(set<string>::iterator it=word.begin();it!=word.end();it++)cnt++;//begin函数返回第一个元素的迭代器
  cout<<cnt;
 }
  

? ? ?这道题是模板题，题目要求统计不重复的不同字符串的个数，我们不仅要知道有多少字符串，还要去重，有什么数据结构能帮我们呢？那必然是哈希表set啊，自带去重功能，多好的STL，我们只需要不断执行insert插入操作，最后遍历统计集合内有多少字符串就可以啦。

4.阅读理解(map和set)

#include<iostream>
#include<set>
#include<map>
#include<string>
using namespace std;
map<string,set<int>>mp;
int n,l,m;
string word,s;
int main()
{
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    cin>>l;
    while(l--)
    {
      cin>>word;
      mp[word].insert(i);
    }
   }
   cin>>m;
   while(m--)
   {
      cin>>s;
      if(mp.count(s))
      {
        for(set<int>::iterator it=mp[s].begin();it!=mp[s].end();it++)
         {
           cout<<*it<<" ";
         }
      }
     cout<<endl;
   }
   return 0;
}

? ? ?这道题对我这种菜鸡来说还是有点难的，首先我们要存储字符串，还要存储字符串的每个单词在哪篇文章出现过，诶，这不是关键字和值的键值对吗？给一个单词，我们就知道它在哪篇文章出现过，而且还不只一篇文章，对应的值是一个集合，那我们的思路就很清晰了。

? ? ?定义一个map，关键字是字符串，也就是单词，值是出现该单词的文章的编号，因为不只一个，是集合，所以定义了一个set集合，之后就是把单词和对应的文章编号不断地插入。插入完成之后，我们就要开始询问了，you这个单词在哪篇文章出现过啊？如果mp.count(you)不等于0，说明存在，那我们就开始遍历mp[you]对应的set集合，输出对应的值即可。

5.求区间和(一维前缀和)

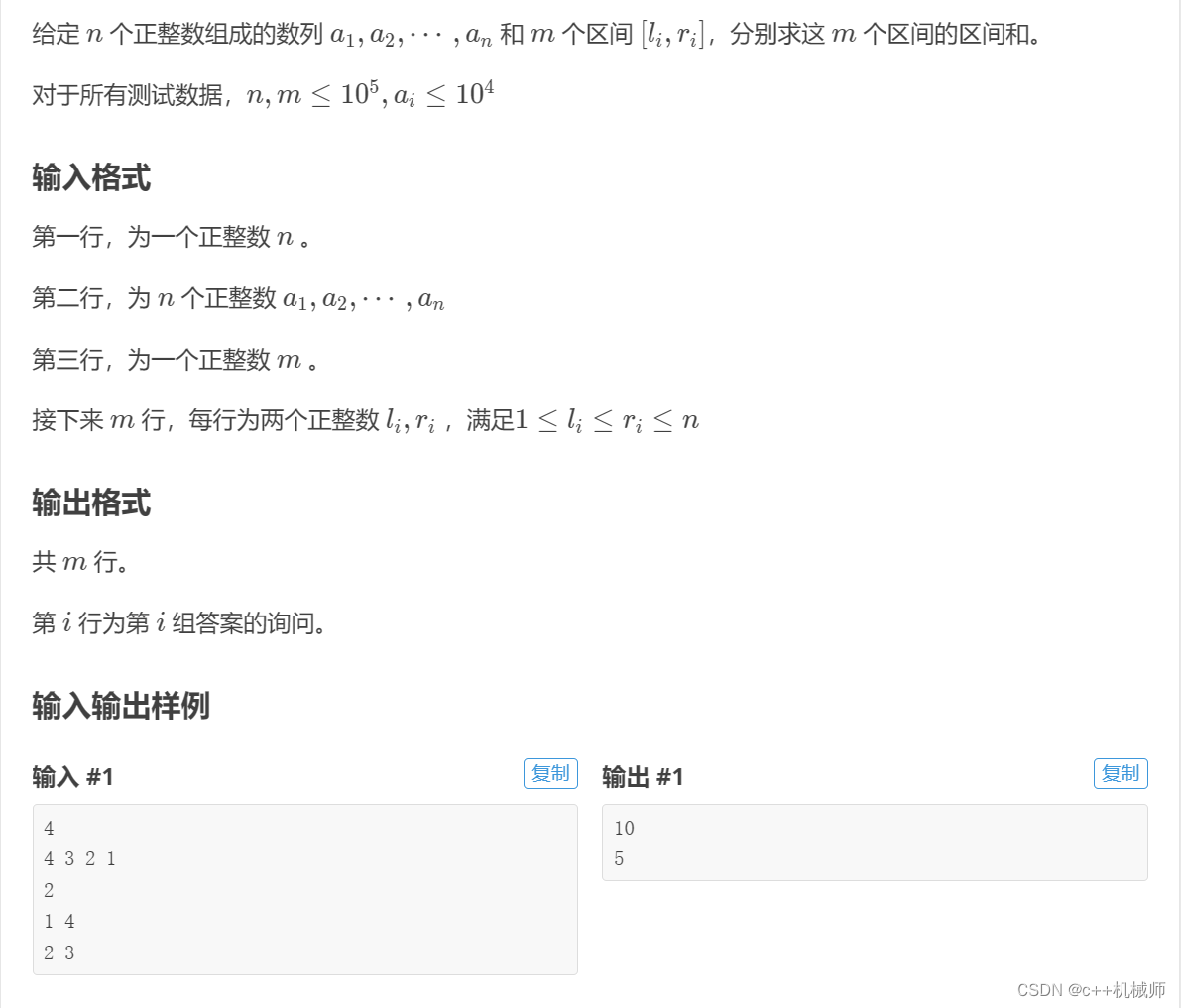
#include<iostream>
using namespace std;
int sum[100010];
int ans[100010];
int a,m,l,r;
int main()
{
  int n;
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    cin>>a;
    ans[i]=a;
  }
   sum[0]=0;
  for(int i=1;i<=n;i++)//求前缀和
  {
   sum[i]=sum[i-1]+ans[i];
  }
   cin>>m;
  for(int i=1;i<=m;i++)//用前缀和求区间和
  {
    cin>>l>>r;
    cout<<sum[r]-sum[l-1]<<endl;
  }
   return 0;
}

? ? ? 这道题也是模板题，先求前缀和，再用前缀和求区间和。

6.最大加权矩形(二维前缀和)

#include<iostream>
using namespace std;
int sum[120][120];
int num[120][120];
int n,m,maxn,s;
int main()
{
  cin>>n;
  for(int i=1;i<=n;i++)
  {
     for(int j=1;j<=n;j++)
     {  
        cin>>m;
        num[i][j]=m;
     }
   }
    for(int i=1;i<=n;i++)
  {
     for(int j=1;j<=n;j++)
     {  
        sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+num[i][j];//求二维前缀和
     }
   } 
    maxn=sum[1][1];
    for(int i=1;i<=n;i++)
{
    for(int j=1;j<=n;j++)
    {
        for(int p=i;p<=n;p++)
        {
        	for(int q=j;q<=n;q++)
        	{
        	    s=sum[p][q]-sum[i-1][q]-sum[p][j-1]+sum[i-1][j-1];//求哪个区间最大
                maxn=max(maxn,s);
            }
        }
    }
}
cout<<maxn;
return 0;
}

? ? ?这道题是求二维前缀和，对应的方法在代码里面标注了，求完二维前缀和后，我们就要开始遍历，求左上角坐标为(i,j)、右下角坐标为(p,q)的矩形的权值，我们可以把每一个点看作是一个方格，这样会更好理解一些，之后就是不断进行比较，最后输出最大值。

7.领地选择(矩形面积固定的二维前缀和)

#include<iostream>
#include<vector>
using namespace std;
int n,m,c,a,s;
int maxn=-0x7fffffff;//一定要初始化一个非常小的值，不然会WA
int x,y;
int sum[1010][1010];
int num[1010][1010];
int main()
{
  cin>>n>>m>>c;
  for(int i=1;i<=n;i++)
  {
     for(int j=1;j<=m;j++)
     {
       cin>>a;
       num[i][j]=a;
     }
  }
  for(int i=1;i<=n;i++)
  {
     for(int j=1;j<=m;j++)
     {
        sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+num[i][j];
     }
   }

  for(int i=c;i<=n;i++)
  {
     for(int j=c;j<=m;j++)
     {
        int s=sum[i][j]-sum[i][j-c]-sum[i-c][j]+sum[i-c][j-c];
        maxn=max(maxn,s);
        if(maxn==s)x=i-c+1,y=j-c+1;//最后要加1，是坑！
     }
   }
  cout<<x<<" "<<y;
  return 0;
 }

? ? ?这道题也是二维前缀和，不同的是这个题要求矩形的面积是固定的，所以代码略有不同，要保证矩形面积是c^2。?