算法通关村第十三关—数论问题(黄金)

?????????????数论问题

一、辗转相除法

?辗转相除法又叫做欧几里得算法，是公元前300年左右的希腊数学家欧几里得在他的著作《几何原本》提出的。最大公约数(greatest common divisor,简写为gcd),是指几个数的共有的因数之中最大的一个，例如8和12的最大公因数是4，记作gcd(8,12)=4。
?辗转相除法最重要的规则是，若r是a÷b的余数，则gcd(a,b)=gcd(b,r)。例如计算gcd(546,429):

由于546=1(429)+117
429=3(117)+78
117=1(78)+39
78=2(39)
因此
gcd(546,429)
=gcd(429,117)
=gcd(117,78)
=gcd(78,39)
=39

循环实现代码

int gcd(inta,intb){//循环实现
    int k = 0;
    do{
        k = a%b;//得到余数
        a = b;//根据辗转相除法，把被除数赋给除数
        b = k;//余数赋给被除数
    }while(k != 0);
    return a;//返?被除数
}

递归实现代码

public int gcd(int x, int y){
    return x == 0 ? y : gcd(y % x, x);
}

二、素数与合数

判断素数与合数的函数

boolean isPrime(int num){
//判断num：从2判断到num^(1/2)即可
int max = (int)Math.sqrt(num);
for (int i = 2; i <= max; i++){
    if (num % i == 0) return false; //合数
}
return true; //素数
}

LeetCode204 给定整数n，返回所有小于非负整数n的质数的数量

public int countPrimes(int n){
int sum = 0;
for (int i = 2; i < n; i++){
    if（isPrime(i)){
        sum++;
    }
    return sum;
}

boolean isPrime(int num){
//判断num：从2判断到num^(1/2)即可
int max = (int)Math.sqrt(num);
for (int i = 2; i <= max; i++){
    if (num % i == 0) return false; //合数
}
return true; //素数
}

三、埃及筛

?上面LeetCode204的题找素数的方法虽然能解决问题，但是效率太低，能否有效率更高一些的方法呢？
?解决这个题有一个有效的方法，叫做埃氏筛，后来又产生了线性筛，奇数筛等改进的方法。
基本思想是如果是质数，那么大于×的y的倍数2X.3x…一定不是质数，因此我们可以从这一点入手。如下图所示：

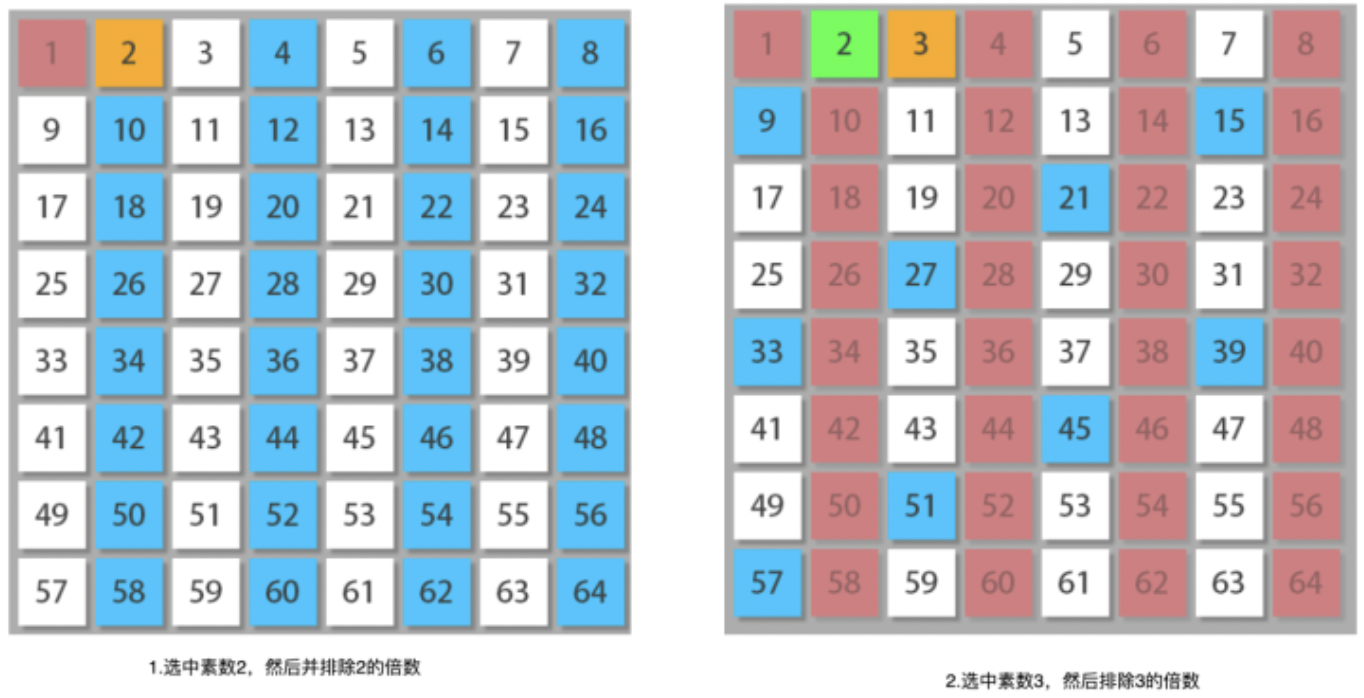
先选中数字2,2是素数，然后将2的倍数全部排除（在数组里将该位置标记为0就行了）。
接着选中数字3,3是素数，然后将3的倍数全部排除。
接着选择数字5,5是素数，然后将5的倍数全部排除。
接着选择7,11,13一直到n，为什么4、6、8、9.不会再选择了呢？因为我们已经在前面的步骤中，将其变成0了。所以实现代码如下：

class Solution {
    public int countPrimes(int n) {
        int[] arr = new int[n];
        int sum = 0;
        for(int i = 2; i < n; i++){
            if(arr[i] == 0){
                sum++;
                for(int j = 2; (long)j * i < n; j++) arr[j * i] = 1;      
            }
        }
        return sum;
    }
}

?当然这里还可以继续优化，对于一个质数 x，如果按上文说的我们从2x开始标记其实是冗余的，应该直接从x?x开始标记，因为 2x,3x,… 这些数一定在 xxx 之前就被其他数的倍数标记过了，例如2的所有倍数，3的所有倍数等。

class Solution {
    public int countPrimes(int n) {
        int[] arr = new int[n];
        int sum = 0;
        for(int i = 2; i < n; i++){
            if(arr[i] == 0){
                sum++;
                if((long)i * i < n)
                for(int j = i * i; j < n; j+= i) arr[j] = 1;      
            }
        }
        return sum;
    }
}

四、丑数问题

?Leetcode263 丑数就是只包含质因数2、3和5的正整数。给你一个整数n，请你判断n是否为丑数。如果是，返回true;否则，返回false

class Solution {
    public boolean isUgly(int n) {
        if(n <= 0) return false;
        while(n % 2 == 0) n /= 2;
        while(n % 3 == 0) n /= 3;
        while(n % 5 == 0) n /= 5;

        return n == 1;
    }
}