机器学习---模型评估

1、混淆矩阵

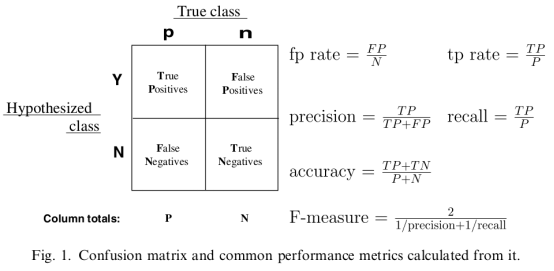
对以上混淆矩阵的解释：

P：样本数据中的正例数。

N：样本数据中的负例数。

Y：通过模型预测出来的正例数。

N：通过模型预测出来的负例数。

True Positives:真阳性，表示实际是正样本预测成正样本的样本数。

Falese Positives:假阳性，表示实际是负样本预测成正样本的样本数。

False Negatives:假阴性，表示实际是正样本预测成负样本的样本数。

True Negatives:真阴性，表示实际是负样本预测成负样本的样本数。

?:真阳性率(True Positive Rate，TPR)，也叫灵敏度(Sensitivity)，召回率(Recall)。即：
?，正确的预测出的正例数占样本中正例总数的比例。真阳性率越大越好，越大代表在正样本中预测为正例的越多。

??:假阳性率(False?Positive Rate，FPR)，也叫误诊率。错误的预测出的正例数占样本中负例的比例。假阳性率越小越好，越小代表在负样本中预测为正例的越少。

?:正确率(Precision),也叫精确率，?，通过模型预测出来真正是正例的正例数占模型预测出来是正例数的比例，越大越好。

?:准确率(accuracy)，?,模型预测正确的例数占总样本的比例。越大越好。

举例：假设现在有60个正样本，40个负样本，我们通过模型找出正样本50个，其中40个是真正的正样本，那么上面几个指标如下：

TP=40	FP=10
FN=20	TN=30

可知，一个模型的TP和TN越大越好。准确率=70/100=70%。精确率=40/50=80%。召回率=40/60=2/3。

2、ROC和AUC:

ROC(Receiver Operating Characteristic)曲线和AUC(Area Under the Curve)值常被用来评价一个二值分类器(binary classifier) 的优劣。

ROC曲线是以假阳性率FPR为横轴，以真阳性率TPR为纵轴的一个曲线图像。图像中的每一点是一个分类阈值，根据一些连续的分类阈值可以得到ROC的图像，如下图：有20个样本，其中真实正例有10个，用p表示，负例有10个，用n表示。Inst# 代表样本编号，Class代表样本真实的类别，Score表示利用模型得出每个测试样本属于真实样本的概率。依次将Score概率从大到小排序，得到下表：

从第一个样本开始直到第20个样本，依次将Score当做分类阈值threshold。当预测测试样本属于正样本的概率大于或等于该threshold时，我们认为该样本是正样本，否则是负样本。

如：拿到第一个样本，该样本真实类别是p,Score=0.9，将0.9看成分类阈值threshold，那么该样本预测是正例，TPR=1/10,FPR=0/10=0，拿到第二个样本，该样本真实类别是p,Score=0.8,将0.8作为threshold,该样本预测是正例，TPR=2/10,FPR=0/10=0 …?…?以此类推,当拿到第7个样本时，该样本真实类别是n,Score=0.53，将0.53看成分类阈值threshold，预测为正例，但是预测错误，将本该属于负例的样本预测为正例，那么当阈值为0.53时，共预测7个样本，预测正确的样本标号为1,2,4,5,6。预测错误的样本标号为：3,7。那么此时，TPR=5/10=0.5,FPR=2/10=0.2。

按照以上方式，每选择一个阈值threshold时，都能得出一组TPR和FPR,即ROC图像上的一点。通过以上，可以得到20组TPF和FPR，可以得到ROC图像如下，当threshold取值越多，ROC曲线越平滑。

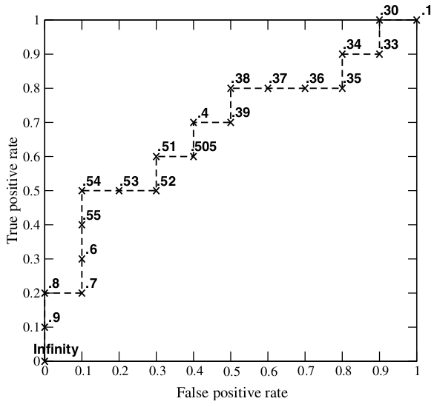
上图图像当样本真实类别为正例时，模型预测该样本为正例那么图像向上画一步（TPR方向）。如果该样本真实类别是负例，模型预测该样本为正例那么图像向右画一步（FPR方向）。

下图中，如果ROC的图像是通过（0,0）点和（1.1）点的一条直线也就是①线，那么当前模型的预测能力是0.5，即：模型在预测样本时，预测对一次，预测错一次，会形成①曲线。如果ROC曲线是②线，那么该模型预测数据的真阳性率大于假阳性率，也就是模型预测对的次数多，预测错的次数少，模型越好。当模型的ROC曲线为③线时，模型的假阳性率比真阳性率大，模型预测错的次数多，预测对的次数少，还不如随机瞎蒙的概率0.5。综上所述，ROC的曲线越是靠近纵轴，越陡，该模型越好。那么如何根据ROC来量化评价一个模型的好坏，这就要用到AUC面积。

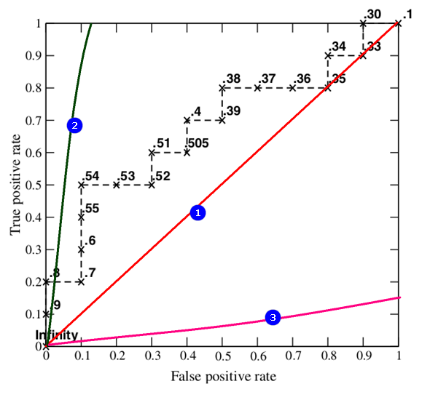
AUC面积是ROC曲线与横轴（假阳性率，FPR）围成的面积,也就是曲线下方的面积。AUC面积越大越好，代表模型分类效果更准确。

计算AUC的公式：

其中，?是属于正例的样本。M：测试样本中的正例数。N：测试样本中的负例数。?代表将测试样本（正例和负例都有）中的Score值按照正序排序，找到样本属于正例的索引号累加和。

AUC=1，完美的分类器，采用这个预测模型时，不管设定什么样的阈值都能正确的预测结果。绝大多数情况下，不存在这种分类器。

0.5<AUC<1,优于随机猜测，可以调节分类阈值，使AUC越靠近1，模型效果越好。

AUC=0.5,和随机分类一样，就是随机瞎蒙，模型没有预测价值。

AUC<0.5,比随机分类还差，大多数情况下成功避开了正确的结果。

AUC这种评估方式较计算准确率的评估方式更好。假设有两个模型M1与M2,两个模型的准确率都是80%，假设默认阈值0.5时，M1模型预测正例的概率多数位于0.51左右，但不小于0.5。M2模型预测正例的概率多数位于0.9附近，那么同样是80%的正确率下，M2模型将结果预测的更彻底，反映到AUC面积中，M2中预测正例的概率多数位于0.9左右,对应的?比较大，相应的AUC值比较大，而M1的AUC相对较小。所以AUC这种评估模型的方式更能说明模型好有多好，能更好的计算模型的纯度。