MATLAB - 使用 TOPP-RA 求解器生成带约束条件的时间最优轨迹

系列文章目录

前言

本例演示如何生成满足速度和加速度限制的轨迹。该示例使用了 contopptraj 函数，该函数使用可达性分析 (RA) 求解受约束的时间最优路径参数化 (TOPP) 轨迹。

一、示例背景

本例解决的是 TOPP 问题，这是一个机器人问题，其目标是在系统约束条件下找到最快的路径。在本例中，您将使用 contopptraj 函数，该函数通过使用一种基于可达性分析（RA）的方法来解决受速度和加速度约束的 TOPP 问题，这种方法被称为 TOPP-RA[1]。解决 TOPP 问题的其他方法依赖于数值积分 (NI) 或凸优化 (CO)。TOPP 的应用包括

• 重新调整机械手的联合空间轨迹，以满足制造商提供的运动学约束。
• 生成联合空间轨迹，在给定计划路径的情况下快速返回最优轨迹。
• 根据移动机器人的运动限制，优化其在 SE(3) 中的移动路径。

您可以通过以下方式使用 contopptraj 函数：

• 在满足速度和加速度限制的前提下，生成一条连接各航点的轨迹。在这种情况下，使用最小运动轨迹作为初始猜测。更多信息，请参阅创建运动学约束轨迹。
• 重新参数化现有轨迹，同时在速度和加速度限制条件下保留其时序。路径由 N 维输入空间中的航点组成，是任意类型的轨迹。然后，contopptraj 函数会在同一时间调整机器人导航路径的方式，将现有轨迹映射为一个能解决 TOPP 问题的新轨迹。

在本例中，您需要更新连接五个 2-D 航点的现有轨迹。初始路径是基于五次多项式的初始轨迹插值，它提供了形状。然后使用 contopptraj 函数对初始路径应用速度和加速度限制。

二、定义航点和初始轨迹

两条轨迹连接同一组航点，并受到一组速度和加速度限制。指定航点。

waypts = (deg2rad(30))*[-1 1 2 -1 -1.5; 1 0 -1 -1.1 1];

?不同的轨迹具有不同的几何和运动属性，这会影响它们在空间中的导航路径。为机械手路径选择轨迹示例说明了机器人系统工具箱?中提供的各种轨迹函数之间的一些差异。

在本示例中，使用五次多项式轨迹连接航点。五次多项式通过使用平滑的速度和加速度曲线来连接线段。

tpts = [0 1 2 3 5];
timeVec = linspace(tpts(1),tpts(end),100);
[q1,qd1,qdd1,pp1] = quinticpolytraj(waypts,tpts,timeVec);

三、使用约束 TOPP-RA 求解器完善轨迹

根据默认参数，五次多项式产生的输出会在每个航点停止。您可以使用 TOPP-RA 求解器计算在速度和加速度受限的情况下，以最快的速度穿越路径，同时仍在每个航点停止。使用 contopptraj 函数生成一条轨迹，以尽可能快的速度穿越初始路径，同时满足指定的速度和加速度限制。

vellim = [-40 40; -25 25]; 
accellim = [-10 10; -10 10];
[q2,qd2,qdd2,t2] = contopptraj(pp1,vellim,accellim,numsamples=100);

将初始轨迹和修改后的轨迹绘制在同一幅图上。请注意 TOPP-RA 求解器是如何在满足已知约束条件的同时加快轨迹速度的。

% Create a figure and adjust the color order so that the second two lines
% have the same color as the associated first two lines
figure
c = colororder("default");
c(3:4,:) = c(1:2,:);
colororder(c)

% Plot results
subplot(3,1,1)
plot(timeVec,q1);
hold on
plot(t2,q2,"--")
legend("Quintic 1","Quintic 2","Constrained 1","Constrained 2")
title("Joint Configuration")
xlim([0 tpts(end)])

subplot(3,1,2)
hold on
plot(timeVec,qd1)
plot(t2,qd2,"--")
title("Joint Velocity")
xlim([0 tpts(end)])

subplot(3,1,3)
hold on
plot(timeVec,qdd1)
plot(t2,qdd2,"--")
title("Joint Acceleration")
xlabel("Time (s)")
xlim([0 tpts(end)])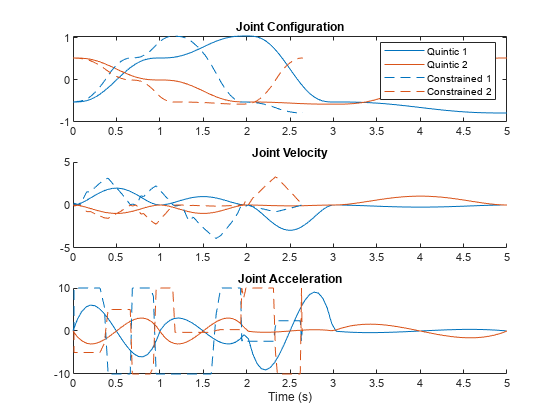

?

参考资料

1. Pham, Hung, and Quang-Cuong Pham. “A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis.”?IEEE Transactions on Robotics, 34, no. 3 (June 2018): 645–59. https://doi.org/10.1109/TRO.2018.2819195.